Assertion: A rocket launched vertically upward explodes at the highest point it reaches. the explosions produces three fragments with non-zero initial velocity. Then, the initial velocity vectors of all the three fragments are in one plane.
Reason For sum of momentum of three particles, all the three momentum vectors must be coplanar.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
To solve the problem, we need to analyze the assertion and the reason provided in the question regarding the explosion of a rocket and the behavior of its fragments.
1. Understanding the Assertion:
- The assertion states that when a rocket is launched vertically upward and explodes at its highest point, it produces three fragments with non-zero initial velocities. It claims that the initial velocity vectors of all three fragments are in one plane.
2. Analyzing the Situation:
- When the rocket reaches its highest point, its vertical velocity becomes zero. At this point, if it explodes, the fragments will have some initial velocities but they will still be influenced by the conditions at that moment (i.e., the vertical motion has ceased).
3. Momentum Conservation:
- According to the law of conservation of momentum, the total momentum before the explosion must equal the total momentum after the explosion.
- Since the rocket is at the highest point, its momentum in the vertical direction is zero. Therefore, the vector sum of the momenta of the fragments must also be zero.
4. Implication of Coplanarity:
- For the total momentum to be zero, the momentum vectors of the fragments must be arranged such that they cancel each other out. This is only possible if the momentum vectors are coplanar (i.e., they lie in the same plane).
- If the fragments have non-zero initial velocities, their momentum vectors must also be in the same plane to satisfy the condition of zero total momentum.
5. Conclusion:
- Thus, the assertion is true: the initial velocity vectors of all three fragments are indeed in one plane.
- The reason is also true: for the sum of the momenta of the three fragments to be zero, their momentum vectors must be coplanar.
6. Final Answer:
- Both the assertion and the reason are true, and the reason correctly explains the assertion.
- The assertion states that when a rocket is launched vertically upward and explodes at its highest point, it produces three fragments with non-zero initial velocities. It claims that the initial velocity vectors of all three fragments are in one plane.
2. Analyzing the Situation:
- When the rocket reaches its highest point, its vertical velocity becomes zero. At this point, if it explodes, the fragments will have some initial velocities but they will still be influenced by the conditions at that moment (i.e., the vertical motion has ceased).
- According to the law of conservation of momentum, the total momentum before the explosion must equal the total momentum after the explosion.
- Since the rocket is at the highest point, its momentum in the vertical direction is zero. Therefore, the vector sum of the momenta of the fragments must also be zero.
- For the total momentum to be zero, the momentum vectors of the fragments must be arranged such that they cancel each other out. This is only possible if the momentum vectors are coplanar (i.e., they lie in the same plane).
- If the fragments have non-zero initial velocities, their momentum vectors must also be in the same plane to satisfy the condition of zero total momentum.
- Thus, the assertion is true: the initial velocity vectors of all three fragments are indeed in one plane.
- The reason is also true: for the sum of the momenta of the three fragments to be zero, their momentum vectors must be coplanar.
- Both the assertion and the reason are true, and the reason correctly explains the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns9videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
A rocket is projected vertically upwords. It explodes at the/ topmost point of its trajectory into three identical fragments . One of the fragments comes straight down in time t 1 while the1 other two land at a time t2 after explosion. Find the height at which the explosion ocurred in terms of t1andt2 ?
 View Solution
View SolutionA bomb initially at rest explodes by it self into three equal mass fragments. The velocities of two fragments are (3ˆi+2ˆj) m/s and (–ˆi–4ˆj) m/s. The velocity of the third fragment is (in m/s)-
View SolutionA projectile of mass 50kg is shot vertically upwards with an initial velocity of 100m/s. After 5s, it explodes into two fragments, one of which having a mass of 20kg travels vertically up with a velocity of 150m/s:
a. What is the velocity of the other fragment that instant?
b.Calculate the sum of rnornenta of fragment 3s after the explosion. What would have been the momentum of the projectile at this instant if there had been no explosion?View SolutionA particle of mass 4m which is at rest explodes into four equal fragments. All four fragments scattered in the same horizontal plane. Three fragments are found to move with velocity v as shown in the figure. The total energy released in the process is
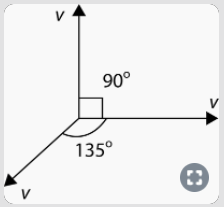 View Solution
View SolutionA shell is fired from a cannon with a speed of 100m/s at an angle 30∘with the vertical (y-direction). At the highest point of its trajectory, the shell explodes into two fragments of masses in the ratio 1:2. The lighter fragment moves vertically upwards with an initial speed of 200m/s. What is the speed of the heavier fragment at the time of explosion?
View SolutionA thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected
 View Solution
View SolutionAn object initially at rest explodes into three equal fragments A,B and C.The momentum of A is pˆi and that of B is √3pˆj
where p is a+ve number. The momentum of C will beView SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A particle is projected from the origin in the x-y plane. The acceleration of particle in negative y-direction is α. If equation of path of the particle is y=ax−bx2, then initial velocity of the particle isView SolutionA projectile is fired with velocity u at an angle θ with horizontal. At the highest point of its trajectory, it splits up into three segments of masses m, m and 2m. First part falls vertically downward with zero initial velocity and second part returns via same path to the point of projection. The velocity of third part of mass 2 m just after explosion will be
View SolutionA small particle of mass m is projected at an angle θ with the x- axis with an initial velocity v0 in the x−yplane as shown in the figure . At a time t<v0sinθg, the angular momentum of the particle is
where ˆi,ˆjandˆk are unit vectors along x,yandz - axis respectively.
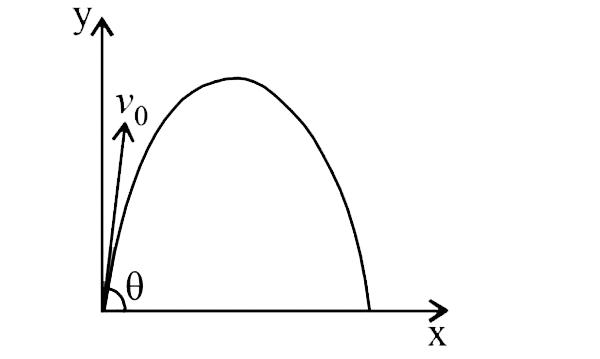 View Solution
View Solution

