Assertion: A given force applied in turn to a number of different masses may cause the same rate of change in momentum in each but not the same acceleration to all.
Reason: and
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:A
To solve the question, we need to analyze the assertion and the reason provided:
Assertion: A given force applied in turn to a number of different masses may cause the same rate of change in momentum in each but not the same acceleration to all.
Reason: F=dpdt and a=Fm
1. Understanding the Assertion:
- The assertion states that if we apply the same force to different masses, they can experience the same rate of change in momentum but will not necessarily have the same acceleration.
- This is based on the relationship between force, mass, and acceleration.
2. Using the Definition of Force:
- According to Newton's second law, force is defined as the rate of change of momentum:
F=dpdt
- Here, dp represents the change in momentum and dt represents the change in time.
3. Applying the Same Force to Different Masses:
- Let’s consider two different masses, m1 and m2.
- If we apply the same force F to both masses, we can write:
F=dp1dtandF=dp2dt
- This implies that the rate of change of momentum for both masses can be equal:
dp1dt=dp2dt
4. Relating Force, Mass, and Acceleration:
- From Newton's second law, we also know:
F=m⋅a
- Rearranging gives us:
a=Fm
- For mass m1:
a1=Fm1
- For mass m2:
a2=Fm2
5. Comparing Accelerations:
- Since m1 and m2 are different, the accelerations a1 and a2 will also be different:
a1≠a2ifm1≠m2
- This shows that while the same force can cause the same rate of change in momentum, it does not result in the same acceleration for different masses.
6. Conclusion:
- Therefore, both the assertion and the reason are correct, and the reason correctly explains the assertion.
Final Answer:
Both the assertion and reason are correct, and the reason is a correct explanation for the assertion.
- The assertion states that if we apply the same force to different masses, they can experience the same rate of change in momentum but will not necessarily have the same acceleration.
- This is based on the relationship between force, mass, and acceleration.
- According to Newton's second law, force is defined as the rate of change of momentum:
F=dpdt
- Here, dp represents the change in momentum and dt represents the change in time.
- Let’s consider two different masses, m1 and m2.
- If we apply the same force F to both masses, we can write:
F=dp1dtandF=dp2dt
- This implies that the rate of change of momentum for both masses can be equal:
dp1dt=dp2dt
- From Newton's second law, we also know:
F=m⋅a
- Rearranging gives us:
a=Fm
- For mass m1:
a1=Fm1
- For mass m2:
a2=Fm2
- Since m1 and m2 are different, the accelerations a1 and a2 will also be different:
a1≠a2ifm1≠m2
- This shows that while the same force can cause the same rate of change in momentum, it does not result in the same acceleration for different masses.
- Therefore, both the assertion and the reason are correct, and the reason correctly explains the assertion.
Both the assertion and reason are correct, and the reason is a correct explanation for the assertion.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Assertion : In rotational plus translational motion of a rigid body, different particles of the rigid body may have different velocities but they will have same accelerations
Reason : Translational motion of a particle is equivalent to the translation motion of a rigid body.
View SolutionStatement I: The greater the rate of the change in the momentum vector, the greater the force applied.
Statement II: Newton's second law is →F=d→pdt.
View SolutionA body of mass 'm' at rest is applied with a force F = (2 + 4t)N. The change in momentum of the interval one second to two second is
View SolutionAssertion: A constant force F is applied on two blocks and one spring system as shown in figure. Velocity of centre of mass increases linearly with time.

Reason: Acceleration of centre of mass is constant.
View SolutionAssertion:- A simple microscope may have different magnification for different persons.
Reasons:- All persons may not have the same near point distance of 25cm
View SolutionAssertion: If a projectile explodes in mid air, linear momentum of center of mass of different fragments remains constant. Reason: Center of mass in this case follows the same path.
View SolutionThe force F acting on a partical of mass m is indicated by the force-time graph shown below. The change in momentum of the particle over time interval from zero to 8 s is.
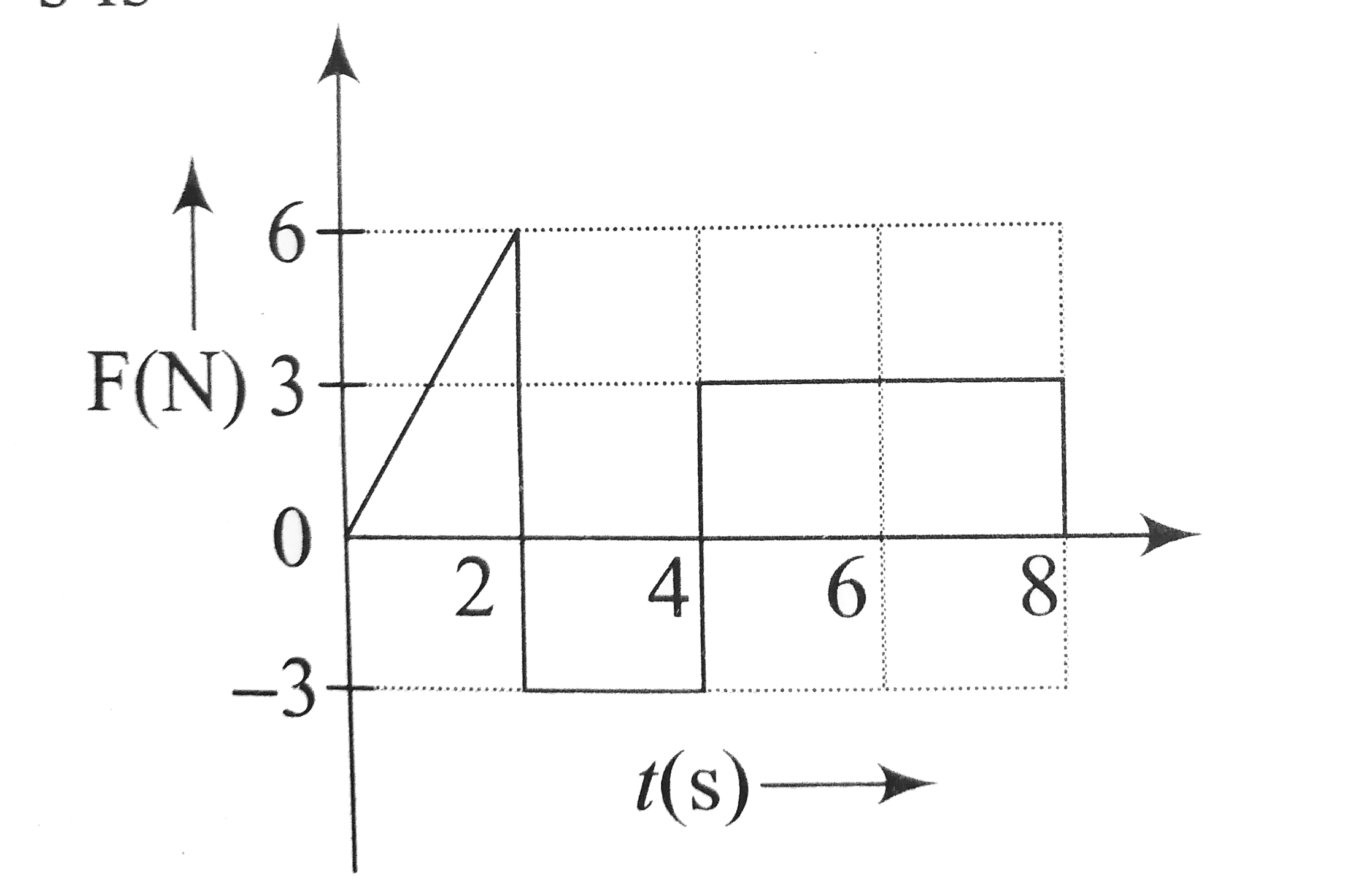
View SolutionAssertion: Two bodies of masses M and m(M>m) are allowed to fall from the same height if the air resistance for each be the same then both the bodies will reach the earth simultaneously.
Reason: For same air resistance, acceleration of both the bodies will be same.
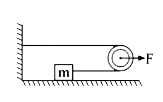
View SolutionIn the given figure the pulley is assumed massless and frictionless. If the friction force on the object of mass m is f, then its acceleration in terms of the force F will be equal to :
View SolutionThe force(F) acting on a particle of mass m changing with time(t) is as shown in (F−t) graph. The change in linear momentum from t=0 to t=6 s (in kN s) is

View Solution
