The sum, difference and cross produce of two vectors A and B are mutually perpendicular if
A and B are perpendicular to each other and |A|=|B|
A and B are perpendicular to each other
A and B are perpendicular but their magnitude are arbitrary
|A|=|B| and their directions are arbitrary
The correct Answer is:D
To determine the conditions under which the sum, difference, and cross product of two vectors A and B are mutually perpendicular, we can follow these steps:
Step 1: Define the vectors
Let:
- R1=A+B
- R2=A−B
- R3=A×B
Step 2: Set up the condition for perpendicularity
For the vectors R1, R2, and R3 to be mutually perpendicular, the following conditions must hold:
- R1⋅R2=0
- R1⋅R3=0
- R2⋅R3=0
Step 3: Calculate the dot product R1⋅R2
Calculating R1⋅R2:
R1⋅R2=(A+B)⋅(A−B)=A⋅A−B⋅B=|A|2−|B|2
Setting this equal to zero gives:
|A|2−|B|2=0⟹|A|=|B|
Step 4: Analyze the direction of vectors
Next, we need to analyze the directions of A and B. Since R1 and R2 are perpendicular, we can visualize this geometrically.
If we assume A and B are perpendicular, we can draw them such that:
- A is along the x-axis.
- B is along the y-axis.
This configuration will ensure that:
- R1 and R2 are at right angles to each other.
Step 5: Conclusion
From the calculations and geometric analysis, we conclude that for the sum, difference, and cross product of two vectors A and B to be mutually perpendicular, the conditions are:
1. A and B must be perpendicular to each other.
2. The magnitudes of A and B must be equal.
Thus, the correct answer is that the sum, difference, and cross product of the vectors are mutually perpendicular if A and B are perpendicular to each other and |A|=|B|.
Let:
- R1=A+B
- R2=A−B
- R3=A×B
For the vectors R1, R2, and R3 to be mutually perpendicular, the following conditions must hold:
- R1⋅R2=0
- R1⋅R3=0
- R2⋅R3=0
Calculating R1⋅R2:
R1⋅R2=(A+B)⋅(A−B)=A⋅A−B⋅B=|A|2−|B|2
Setting this equal to zero gives:
|A|2−|B|2=0⟹|A|=|B|
Next, we need to analyze the directions of A and B. Since R1 and R2 are perpendicular, we can visualize this geometrically.
- A is along the x-axis.
- B is along the y-axis.
- R1 and R2 are at right angles to each other.
From the calculations and geometric analysis, we conclude that for the sum, difference, and cross product of two vectors A and B to be mutually perpendicular, the conditions are:
1. A and B must be perpendicular to each other.
2. The magnitudes of A and B must be equal.
Topper's Solved these Questions
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE
17 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN
6 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
Similar Questions
Knowledge Check
If ˆi,ˆj,ˆk are unit vectors along three mutually perpendicular directions, then
Aˆi.ˆj=1Bˆi׈j=1Cˆi.ˆk=0Dˆi׈k=0
When can you say that two vectors →Aand→B are (a) parallel and (b) perpendicular .
View SolutionThe sum and diffrence of two perpendicular vector of equal length are
View SolutionIf a vector →a is expressed as the sum of two vectors →α and →β along and perpendicular to a given vector →b then →β is equal to
View SolutionTwo vectors →P and →Q that are perpendicular to each other if :
View SolutionThree identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
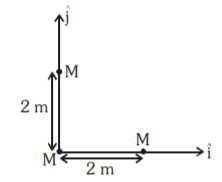
View Solution→aand→b are two unit vectors that are mutually perpendicular. A unit vector that if equally inclined to →a,→band→a×→b is equal to
View SolutionGiven that →aand →b are unit vectors. If the vectors →p=3→a−5→b and →q=→a+→b are mutually perpendicular, then
View Solution
