During uniform circular motion of a particle
distance-time graph is a straight line
distance-time graph is a parabola
displacement-time graph is a straight line
displacement-time graph is a parabola
The correct Answer is:A
To solve the question regarding uniform circular motion and the corresponding graphs, we will analyze the properties of distance and displacement in this context.
1. Understanding Uniform Circular Motion:
- In uniform circular motion, a particle moves along a circular path with a constant speed. The direction of the particle's velocity is continuously changing, which means the particle is accelerating even though its speed is constant.
2. Distance Travelled:
- The distance travelled by the particle in a given time t can be calculated using the formula:
Distance=Speed×Time
- Since the speed v is constant, the distance travelled is directly proportional to the time taken. This means:
Distance∝Time
3. Distance-Time Graph:
- Since distance is directly proportional to time, the graph of distance vs. time will be a straight line passing through the origin. This confirms that option 1 (distance-time graph is a straight line) is correct.
4. Displacement in Circular Motion:
- Displacement is defined as the shortest distance from the initial position to the final position. In circular motion, as the particle moves, the displacement can vary significantly depending on the position of the particle on the circle.
- For example, if the particle moves from point A to point B, the displacement is the straight line connecting these two points.
5. Displacement-Time Graph:
- As the particle continues to move in a circular path, the displacement does not increase uniformly. It can increase and then decrease depending on the position of the particle. Therefore, the displacement-time graph will not be a straight line.
- Instead, it will exhibit a non-linear pattern, which could resemble a parabolic shape but not strictly follow a parabolic equation. Thus, option 3 (displacement-time graph is a straight line) is incorrect, and option 4 (displacement-time graph is a parabola) is also incorrect.
6. Conclusion:
- The only correct option is that the distance-time graph is a straight line, while the displacement-time graph does not follow a simple linear or parabolic form.
Final Answer:
- The correct option is that the distance-time graph is a straight line (Option 1).
- In uniform circular motion, a particle moves along a circular path with a constant speed. The direction of the particle's velocity is continuously changing, which means the particle is accelerating even though its speed is constant.
- The distance travelled by the particle in a given time t can be calculated using the formula:
Distance=Speed×Time
- Since the speed v is constant, the distance travelled is directly proportional to the time taken. This means:
Distance∝Time
- Since distance is directly proportional to time, the graph of distance vs. time will be a straight line passing through the origin. This confirms that option 1 (distance-time graph is a straight line) is correct.
- Displacement is defined as the shortest distance from the initial position to the final position. In circular motion, as the particle moves, the displacement can vary significantly depending on the position of the particle on the circle.
- For example, if the particle moves from point A to point B, the displacement is the straight line connecting these two points.
- As the particle continues to move in a circular path, the displacement does not increase uniformly. It can increase and then decrease depending on the position of the particle. Therefore, the displacement-time graph will not be a straight line.
- Instead, it will exhibit a non-linear pattern, which could resemble a parabolic shape but not strictly follow a parabolic equation. Thus, option 3 (displacement-time graph is a straight line) is incorrect, and option 4 (displacement-time graph is a parabola) is also incorrect.
- The only correct option is that the distance-time graph is a straight line, while the displacement-time graph does not follow a simple linear or parabolic form.
- The correct option is that the distance-time graph is a straight line (Option 1).
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Comprehension
Explore 13 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Matrix Matching
Explore 7 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:JEE Advanced
Explore 24 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
Knowledge Check
In uniform circular motion
AAcceleration is constantBMagnitude of acceleration is contantCTangential acceleration is zeroDTangential acceleration is not zeroFor a particle performing uniform circular motion, choose the incorrect statement form the following.
AMagnitude of particle velocity (speed) remains constant.BParticle velocity remains directed perpendicular to radius vector.CDirection of acceleration keeps changing as particle moves.DMagnitudes of acceleration does not remain constant.
In uniform circular motion
View SolutionA particle performing uniform circular motion has
View SolutionAssertion: A uniform circular motion is an acceleration motion.
Reason: Direction of acceleration is parallel to velocity vector.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
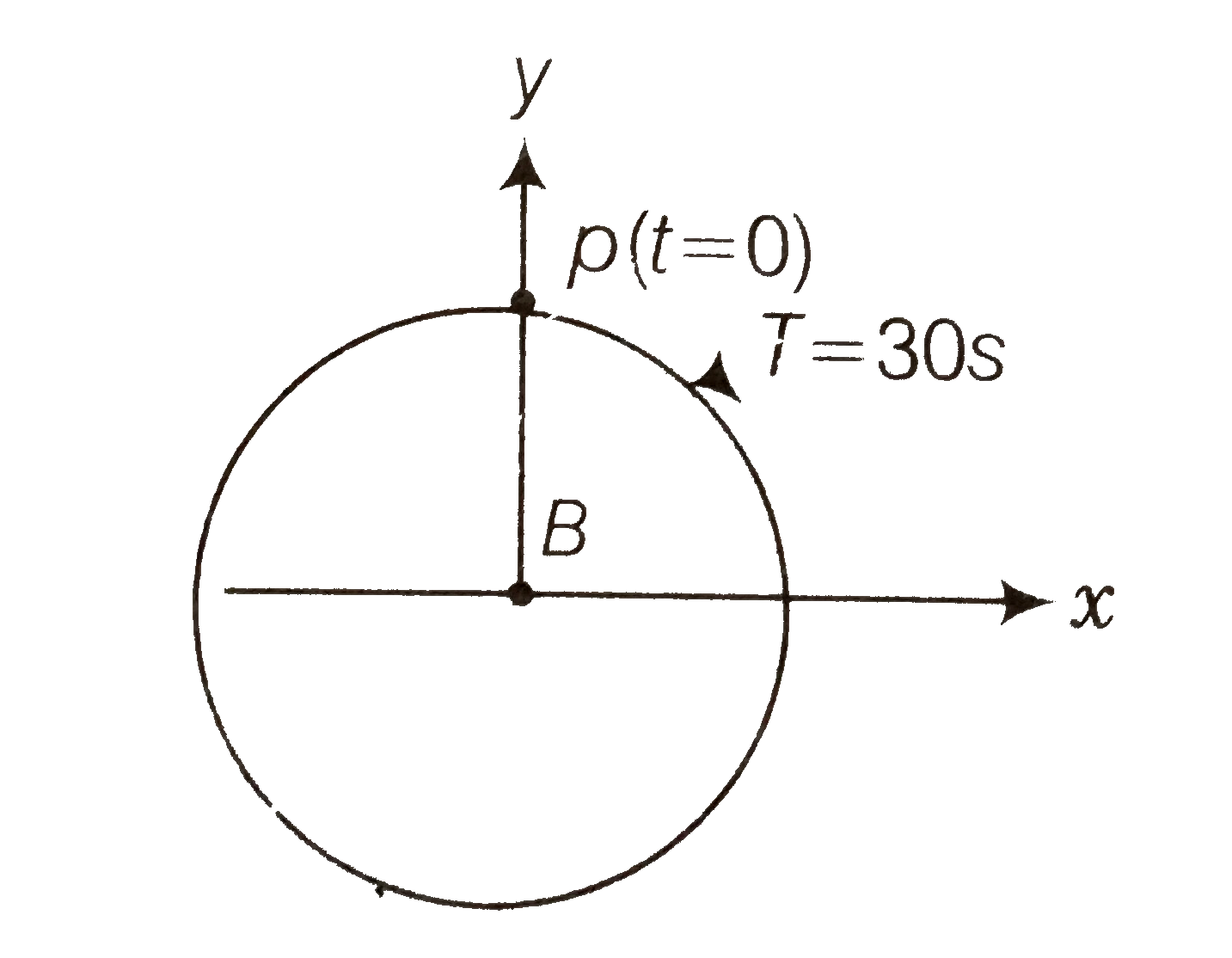
View SolutionUniform circular motion is an example of
View SolutionFor a particle performing uniform circular motion, choose the correct statement (s) from the following.
View Solution