A particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
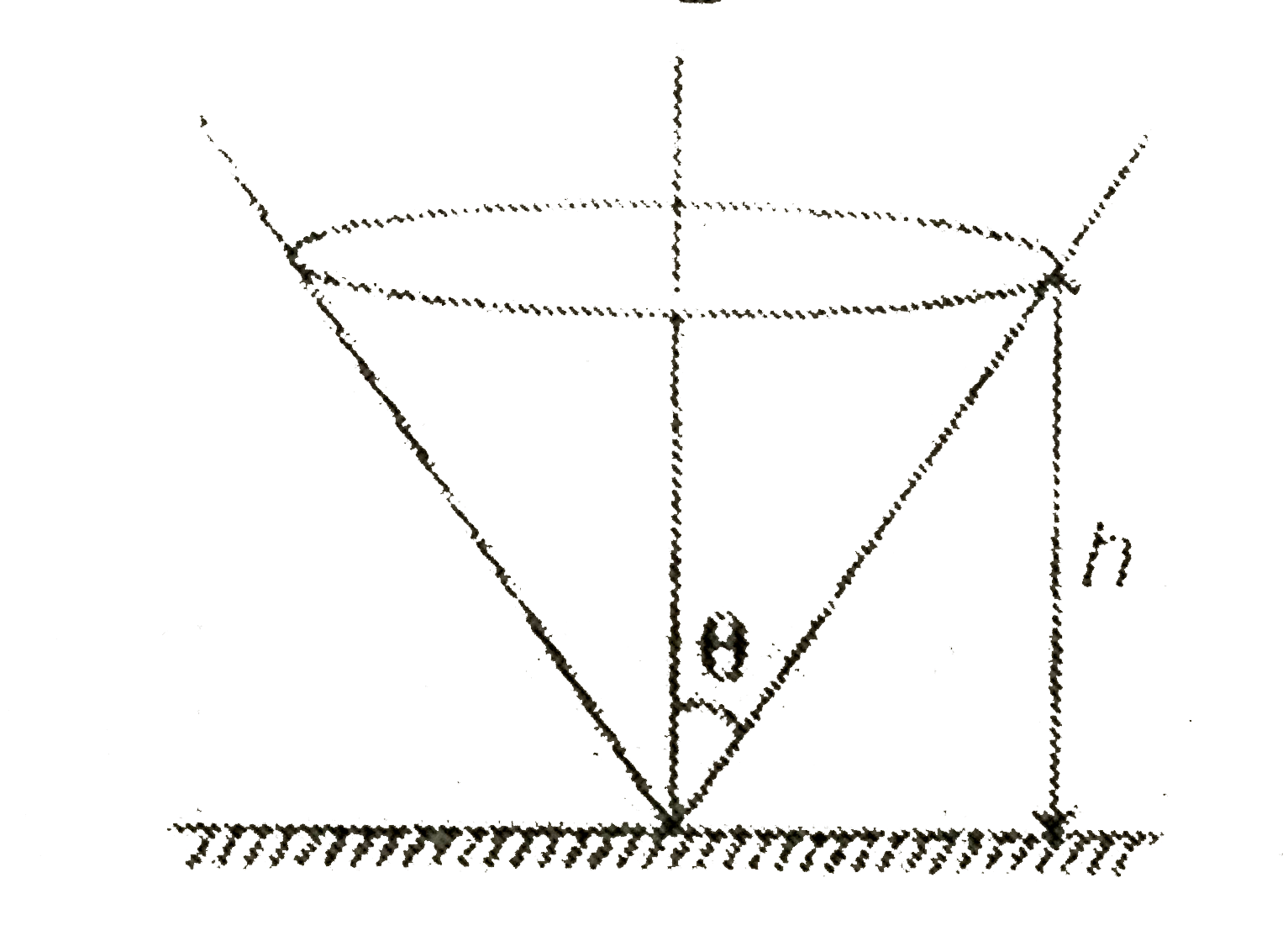
Normal force on particle by surface of cone is mgcosθ
Normal force on particle by surface of cone is mgcosecθ
Time period of revolution of particle increases, if θ increase keeping h constant
Time period of revlution increases, if h increases keeping θ fixed.
The correct Answer is:B, C, D
Step by step video & image solution for A particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is theta, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Matrix Matching
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Advanced
24 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−1/r2) , the total energy is
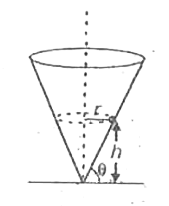
View SolutionA particle describes a horizontal circle of radius r on the smooth surface of an inverted cone as shown. The height of plane of circle above vertex is h. The speed of particle should be
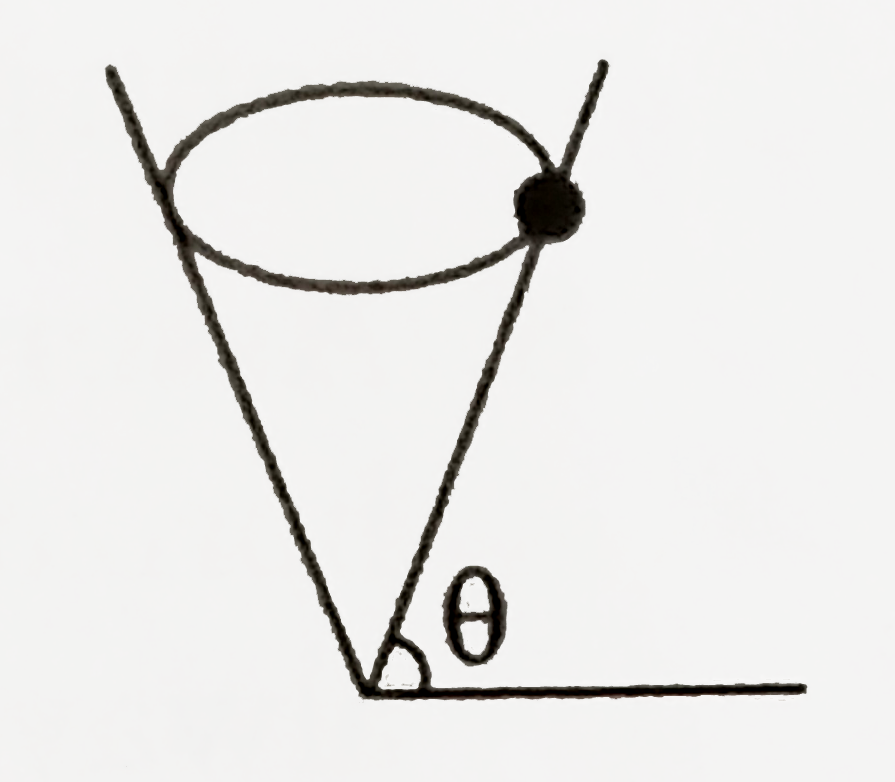
View SolutionAssertion A small block of mass m is rotating in a circle inside a smooth cone as shown in figure. In this case the normal reaction,
N≠mg cosθ
Reason In this case, acceleraion of the block is not along the surface of cone. It is horizontal.
View SolutionA particle describes a horizontal circle on the smooth surface of an inverted cone, the height of the plane of the circle above the vertex is 9.8 cm. Find the speed of the particle (g= 9.8m/s2) [See Fig.] (a) given in the answer section]
View SolutionIn a conical pendulum a small mass is revolving in horizontal circle with constant speed v at the end of the cord of length L that makes an angle θ with the vertical as shown . The value of angle θ would be (where r is the radius of circle)

View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.

View SolutionA particle of mass m comes down on a smooth inclined plane from point B at a height of h from rest. The magni-tude of change in momentum of the particle between position A (just before arriving on horizontal surface) and C (assuming the angle of inclination of the plane as θ with respect to the horizontal) is

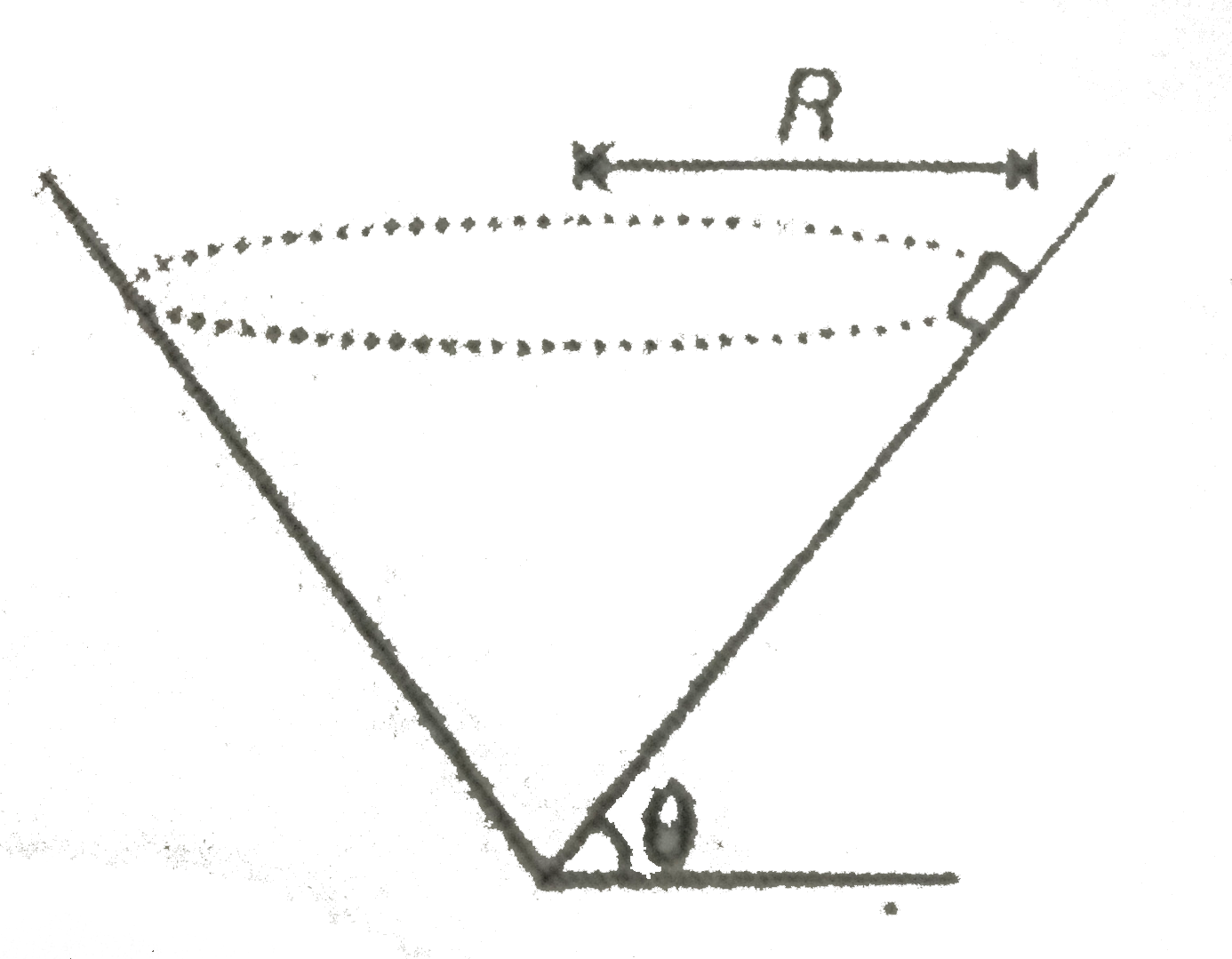
View SolutionA block of mass m is moving in a circle of radius R with speed v inside a smooth cone as shown in figure. Choose the wrong options
View SolutionA ball of mass 'm' is rotating in a circle of radius 'r' with speed v inside a smooth cone as shown in figure. Let N be the normal reaction on the ball by the cone .then choose the wrong option.

View SolutionA particle is describing circular motion in a horizontal plane in contact with the smooth surface of a fixed rigid circular cone with its axis vertical and vertex down. The heigh of the plane of motion above the vertex is hh and the semi-vertical angle of the cone is α The period of revolution of the particle

View Solution
