A pendulum is released from point A as shown in figure. At some instant net force one the bob is making an angle θ with the string. Then Match the following

Table-1Table-2(A)For θ=30∘(P)Particle may be moving along BA(B)For θ=120∘(Q)Particle may be moving along CB(C)For θ=90∘(R)Particle may be at A(D)For θ=0∘(S)Particle is at B(T)None
The correct Answer is:(A)QP,(B)T,(C)R,(D)S
Step by step video & image solution for A pendulum is released from point A as shown in figure. At some instant net force one the bob is making an angle theta with the string. Then Match the following {:(,"Table-1",,"Table-2"),("(A)","For "theta=30^(@),"(P)","Particle may be moving along BA"),("(B)","For "theta=120^(@),"(Q)","Particle may be moving along CB"),("(C)","For "theta=90^(@),"(R)","Particle may be at A"),("(D)","For "theta=0^(@),"(S)","Particle is at B"),(,,"(T)","None"):} by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
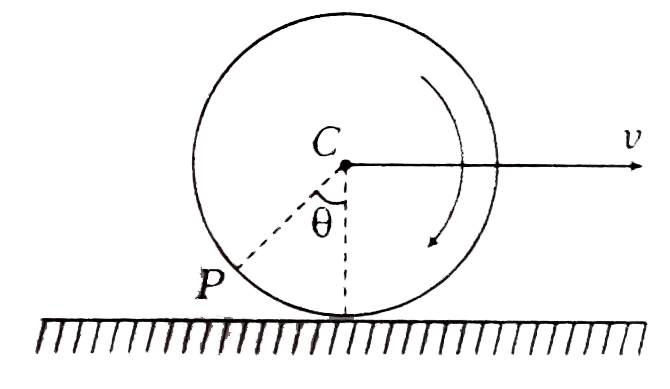
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionA vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionFind the minimum speed at A so that the ball can reach at point B as shown in figure. Also discuss the motion of particle when T=0, v=0 simultaneously at θ=90∘
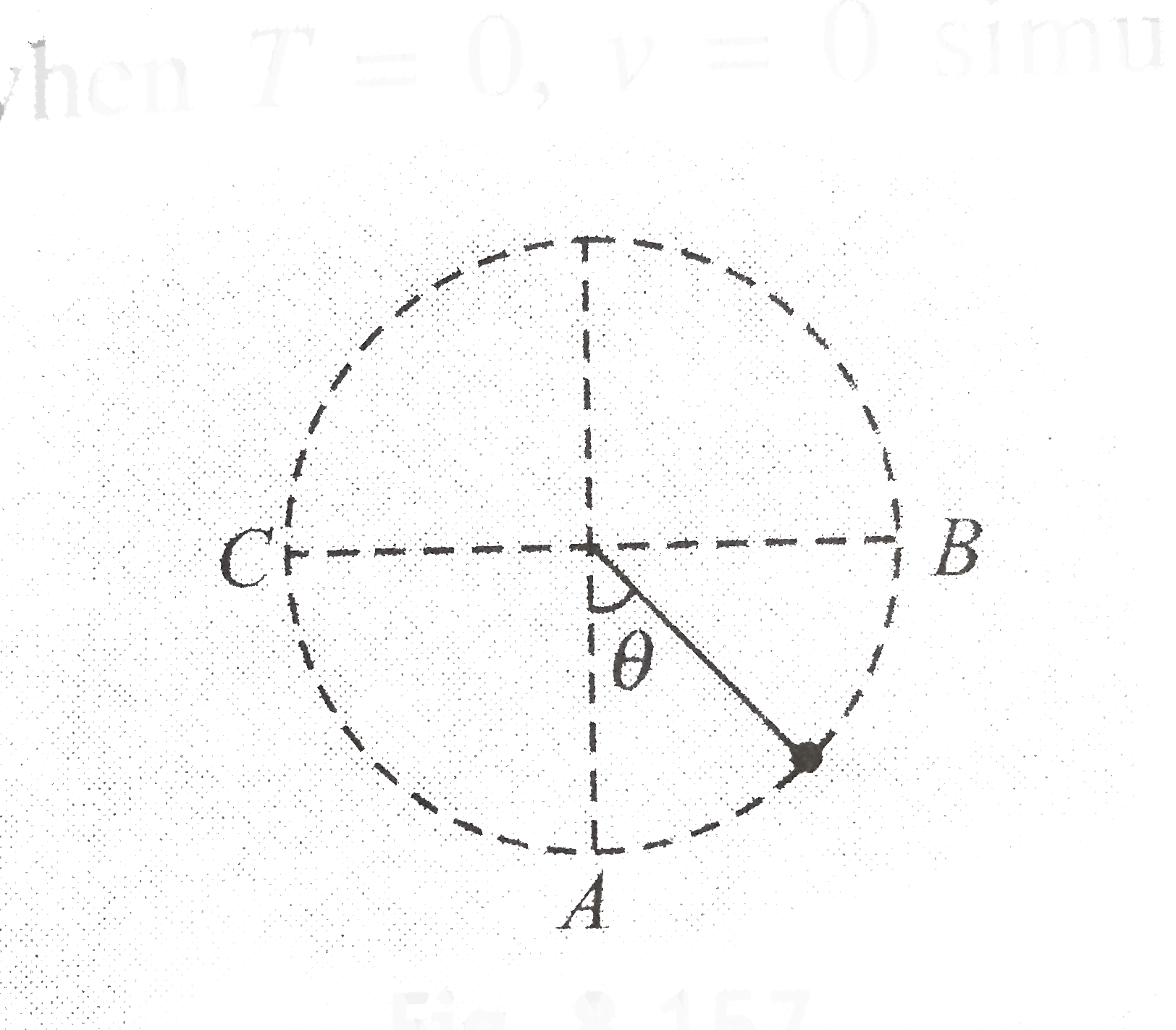
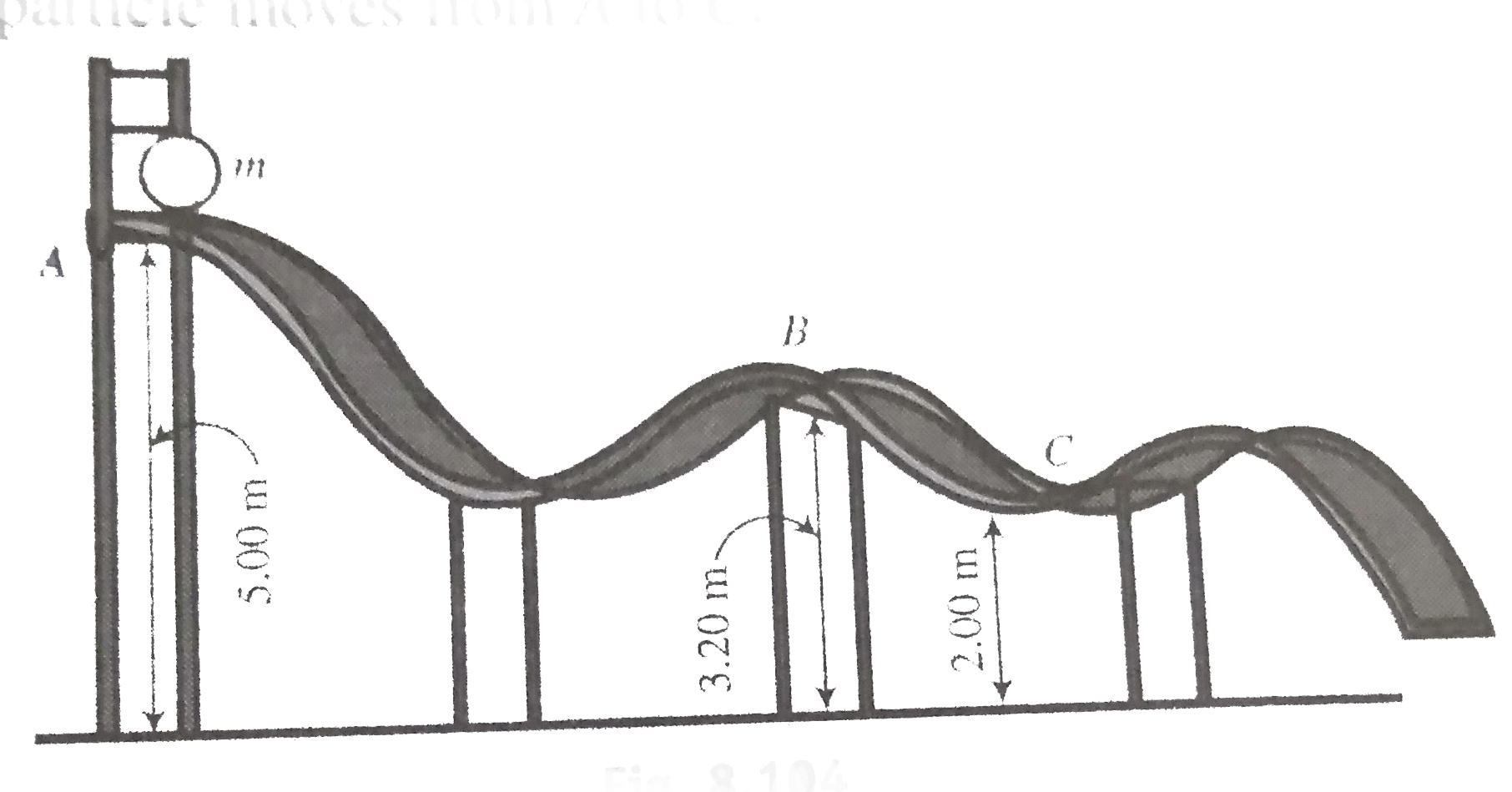
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View SolutionA wedge of height 'h' is released from rest with a light particle P placed on it as shown. The wedge slides down an incline which makes an angle theta with the horizontal. All the surface are smooth, P will reach the surface of the incline in time:

View SolutionA wedge of height 'h' is released from rest with a light particle P placed on it as shown. The wedge slides down an incline which makes an angle theta with the horizontal. All the surface are smooth, P will reach the surface of the incline in time:

View SolutionA particle is moving with speed v=2t2 on the circumference of a circle of radius R. Match the quantities given in Table-1 with corresponding results in Table-2
Table-1Table-2(A)Magnitude to tangential acceleration of particle(P)decreases with time(B)Magnitude of centripetal acceleration of particle(Q)increases with time(C)Magnitude of angular speed of particle with respect to centre of circle(R)remains constant(D)Angle between the total acceleration and centripetal acceleration of partilce(S)depends upon the value of radius R
View Solution
