A solid uniform disc of mass m rolls without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
2 ma
32 ma
ma
12 ma
The correct Answer is:D
To solve the problem of finding the frictional force on a solid uniform disc rolling down an inclined plane, we can follow these steps:
1. Identify the Forces Acting on the Disc:
- The weight of the disc, mg, acts vertically downward.
- This weight can be resolved into two components:
- The component parallel to the incline: mgsinθ
- The component perpendicular to the incline: mgcosθ
2. Set Up the Equations of Motion:
- The vertical component mgcosθ is balanced by the normal force N.
- The net force acting down the incline is given by:
Fnet=mgsinθ−F
- Here, F is the frictional force acting up the incline.
3. Relate Linear Acceleration to Angular Acceleration:
- Since the disc rolls without slipping, the linear acceleration a is related to the angular acceleration α by:
a=Rα
- Thus, we can express α as:
α=aR
4. Apply the Torque Equation:
- The torque τ acting on the disc due to the frictional force is given by:
τ=F⋅R
- This torque is also equal to the moment of inertia I times the angular acceleration α:
τ=Iα
- For a solid disc, the moment of inertia I about its center is:
I=12mR2
5. Equate Torque Expressions:
- Setting the two expressions for torque equal gives:
F⋅R=12mR2⋅aR
- Simplifying this, we get:
F⋅R=12maR
- Dividing both sides by R (assuming R≠0):
F=12ma
6. Conclusion:
- The frictional force F acting on the disc due to the surface of the inclined plane is:
F=12ma
Final Answer:
The frictional force on the disc due to the surface of the plane is 12ma.
- The weight of the disc, mg, acts vertically downward.
- This weight can be resolved into two components:
- The component parallel to the incline: mgsinθ
- The component perpendicular to the incline: mgcosθ
- The vertical component mgcosθ is balanced by the normal force N.
- The net force acting down the incline is given by:
Fnet=mgsinθ−F
- Here, F is the frictional force acting up the incline.
- Since the disc rolls without slipping, the linear acceleration a is related to the angular acceleration α by:
a=Rα
- Thus, we can express α as:
α=aR
- The torque τ acting on the disc due to the frictional force is given by:
τ=F⋅R
- This torque is also equal to the moment of inertia I times the angular acceleration α:
τ=Iα
- For a solid disc, the moment of inertia I about its center is:
I=12mR2
- Setting the two expressions for torque equal gives:
F⋅R=12mR2⋅aR
- Simplifying this, we get:
F⋅R=12maR
- Dividing both sides by R (assuming R≠0):
F=12ma
- The frictional force F acting on the disc due to the surface of the inclined plane is:
F=12ma
The frictional force on the disc due to the surface of the plane is 12ma.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A solid uniform disc of mass m rols without slipping down a fixed inclined plank with an acceleration a. The frictional force on the disc due to surface of the plane is
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View Solution
Knowledge Check
A cylinder of radius R and mass M rolls without slipping down a plane inclined at an angle θ. Coeff. of friction between the cylinder and the plane is μ. For what maximum inclination θ, the cylinder rolls without slipping ?
Atanθ gt 3μsBtanθ ≤ 3μsCtanθ lt 3μsDNone of theseA solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A1/3 g sinθB2/3 g sinθC2/5 g sinθD2/7 g sinθ
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View SolutionA solid sphere of mass m rolls without slipping on an inlined plane of inclination 0. what shoul be the minimum coefficient of static feiction to support pure rolling?
View SolutionWhen a body rolls without sliding up an inclined plane the frictional force is :
View Solution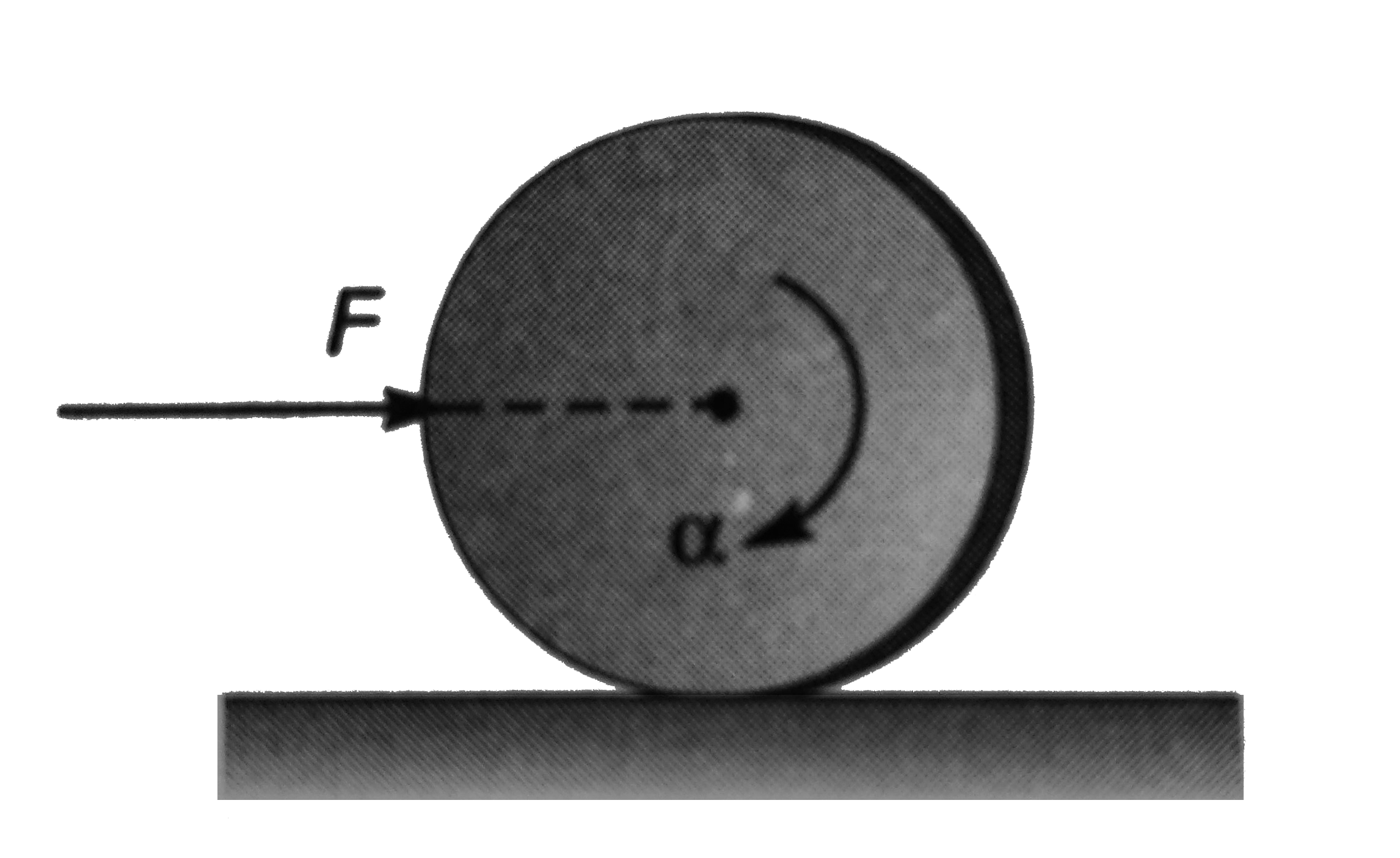
Consider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The magnitude of frictional force acting on the disc is
View SolutionConsider a uniform disc of mass m, radius r rolling without slipping on a rough surface with linear acceleration a and angular acceleration α due to an external force F as shown in the figure coefficient of friction is μ.
Q. The work done by the frictional force at the instant of pure rolling is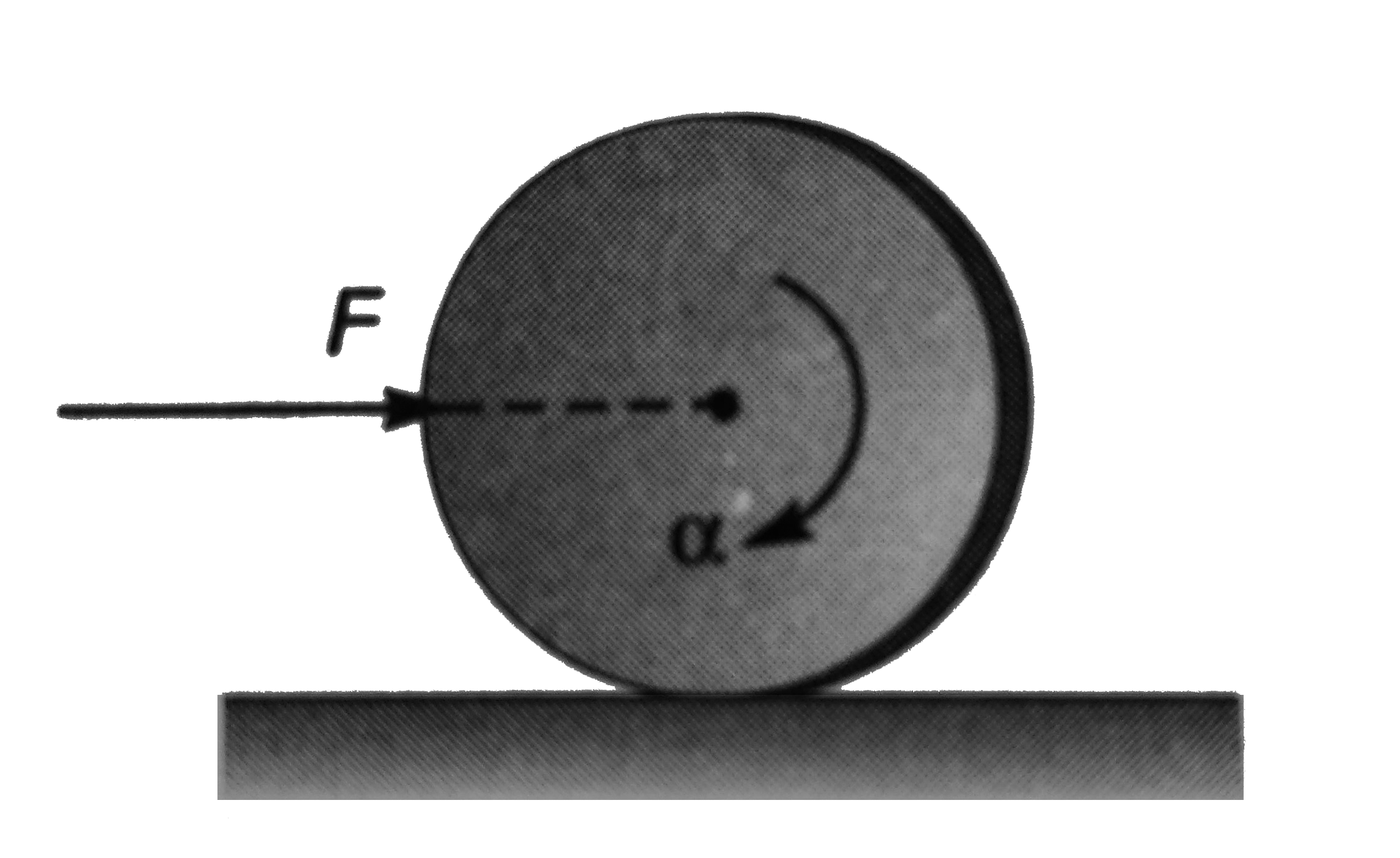
View Solution
