A horizontally force of 12 N pushes a 0.5kg book against a vertical wall. The book is initially at rest. If the coefficent of friction are μk=0.6 and μs=0.8 which of the following statements is true?
The magnitude of the frictional force is 5N
The magnitude of the frictional force is 7.2N
The normal force is 5N
The book will start moving and accelerated
The correct Answer is:a
To solve the problem, we need to analyze the forces acting on the book when a horizontal force of 12 N is applied against a vertical wall. We will determine the frictional force and check which of the given statements is true.
1. Identify the Forces Acting on the Book:
- The weight of the book (mg) acting downward.
- The applied horizontal force (F) of 12 N pushing the book against the wall.
- The normal force (N) exerted by the wall on the book, acting horizontally away from the wall.
- The frictional force (f) acting upward to prevent the book from sliding down.
2. Calculate the Weight of the Book:
m=0.5kg
g=10m/s2
Weight (mg)=m⋅g=0.5⋅10=5N
3. Determine the Normal Force:
- The normal force (N) is equal to the applied horizontal force (F) since the book is in equilibrium in the horizontal direction.
N=F=12N
4. Calculate the Maximum Static Friction:
μs=0.8(coefficient of static friction)
fmax=μs⋅N=0.8⋅12=9.6N
5. Compare the Weight of the Book with Maximum Static Friction:
- The weight of the book (5 N) is less than the maximum static friction (9.6 N). Therefore, the book will not slide down.
6. Determine the Actual Frictional Force:
- Since the book is at rest and only 5 N of force is required to balance the weight, the actual frictional force (f) will be equal to the weight of the book.
f=5N
7. Conclusion:
- The frictional force acting on the book is 5 N, which is sufficient to keep the book at rest against the wall.
Final Answer:
The correct statement is: The magnitude of frictional force is 5 N.
- The weight of the book (mg) acting downward.
- The applied horizontal force (F) of 12 N pushing the book against the wall.
- The normal force (N) exerted by the wall on the book, acting horizontally away from the wall.
- The frictional force (f) acting upward to prevent the book from sliding down.
m=0.5kg
g=10m/s2
Weight (mg)=m⋅g=0.5⋅10=5N
- The normal force (N) is equal to the applied horizontal force (F) since the book is in equilibrium in the horizontal direction.
N=F=12N
μs=0.8(coefficient of static friction)
fmax=μs⋅N=0.8⋅12=9.6N
- The weight of the book (5 N) is less than the maximum static friction (9.6 N). Therefore, the book will not slide down.
- Since the book is at rest and only 5 N of force is required to balance the weight, the actual frictional force (f) will be equal to the weight of the book.
f=5N
- The frictional force acting on the book is 5 N, which is sufficient to keep the book at rest against the wall.
The correct statement is: The magnitude of frictional force is 5 N.
Similar Questions
In Fig the block are at rest a force of 10N act on the block of 4kg mass .The coefficient of staic friction and the coefficient of kinetic friction are μs=0.2andμs=0.15 for both the surface in contact The magnitudeof frcition force acting between the surface of contact between the 2kg and 4kg block in this situation is
 View Solution
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 View Solution
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
 View Solution
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
 View Solution
View SolutionA horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient of friction between the block and the wall is 0.2. the weight of the block is (g=10m/s2)
 View Solution
View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :
View SolutionA body is pushed against vertical wall as shown. If the coefficient of friction between the body and the wall is 0.5, the magnitude of acceleration of the block is 10 K. Where K is
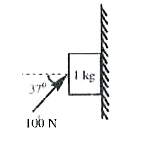 View Solution
View SolutionA block of mass 0.1 kg is held against a wall applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is :
View SolutionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
View SolutionA 1 kg block is being pushed against a wall by a force F=75N as shown in the figure. The coefficient of friction is 0.25. The magnitude of acceleration of the block is:
 View Solution
View Solution

