A ball of mass m approaches a wall of mass M (M>>m), with speed 2 ms−1 along the normal to the wall. The speed of wall is 1 ms−1 towards the ball. The speed of the ball after an elastic collision with the wall is-
5ms−1 away from the wall
9ms−1 away from the wall
3ms−1 away from the wall
4ms−1 away from the wall
The correct Answer is:D
To solve the problem of finding the speed of the ball after an elastic collision with the wall, we can follow these steps:
Step 1: Understand the initial conditions
- The mass of the ball is m.
- The mass of the wall is M (where M≫m).
- The initial speed of the ball is ub=2m/s towards the wall.
- The initial speed of the wall is uw=1m/s towards the ball.
Step 2: Determine the velocity of approach
The velocity of approach is the sum of the speeds of both the ball and the wall since they are moving towards each other. Thus, we have:
Velocity of approach=ub+uw=2+1=3m/s
Step 3: Use the coefficient of restitution
For an elastic collision, the coefficient of restitution e is equal to 1. The formula for the coefficient of restitution is:
e=Velocity of separationVelocity of approach
Since e=1, we can write:
Velocity of separation=Velocity of approach=3m/s
Step 4: Determine the final velocities
After the collision, the ball will rebound away from the wall. Let v be the final speed of the ball after the collision. The wall continues to move towards the ball at 1m/s.
The velocity of separation can be expressed as:
v−(−uw)=v+1
Setting this equal to the velocity of approach:
v+1=3
Step 5: Solve for v
Now, we can solve for v:
v+1=3⟹v=3−1=2m/s
Step 6: Consider the direction
Since the ball is rebounding away from the wall, we need to consider the direction. The ball was initially moving towards the wall (positive direction) and after the collision, it will move in the opposite direction (negative direction). Therefore, the final speed of the ball will be:
v=−2m/s
Conclusion
The speed of the ball after the elastic collision with the wall is 2m/s away from the wall.
---
- The mass of the ball is m.
- The mass of the wall is M (where M≫m).
- The initial speed of the ball is ub=2m/s towards the wall.
- The initial speed of the wall is uw=1m/s towards the ball.
The velocity of approach is the sum of the speeds of both the ball and the wall since they are moving towards each other. Thus, we have:
Velocity of approach=ub+uw=2+1=3m/s
For an elastic collision, the coefficient of restitution e is equal to 1. The formula for the coefficient of restitution is:
e=Velocity of separationVelocity of approach
Since e=1, we can write:
Velocity of separation=Velocity of approach=3m/s
After the collision, the ball will rebound away from the wall. Let v be the final speed of the ball after the collision. The wall continues to move towards the ball at 1m/s.
v−(−uw)=v+1
Setting this equal to the velocity of approach:
v+1=3
Now, we can solve for v:
v+1=3⟹v=3−1=2m/s
Since the ball is rebounding away from the wall, we need to consider the direction. The ball was initially moving towards the wall (positive direction) and after the collision, it will move in the opposite direction (negative direction). Therefore, the final speed of the ball will be:
v=−2m/s
The speed of the ball after the elastic collision with the wall is 2m/s away from the wall.
Similar Questions
A ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
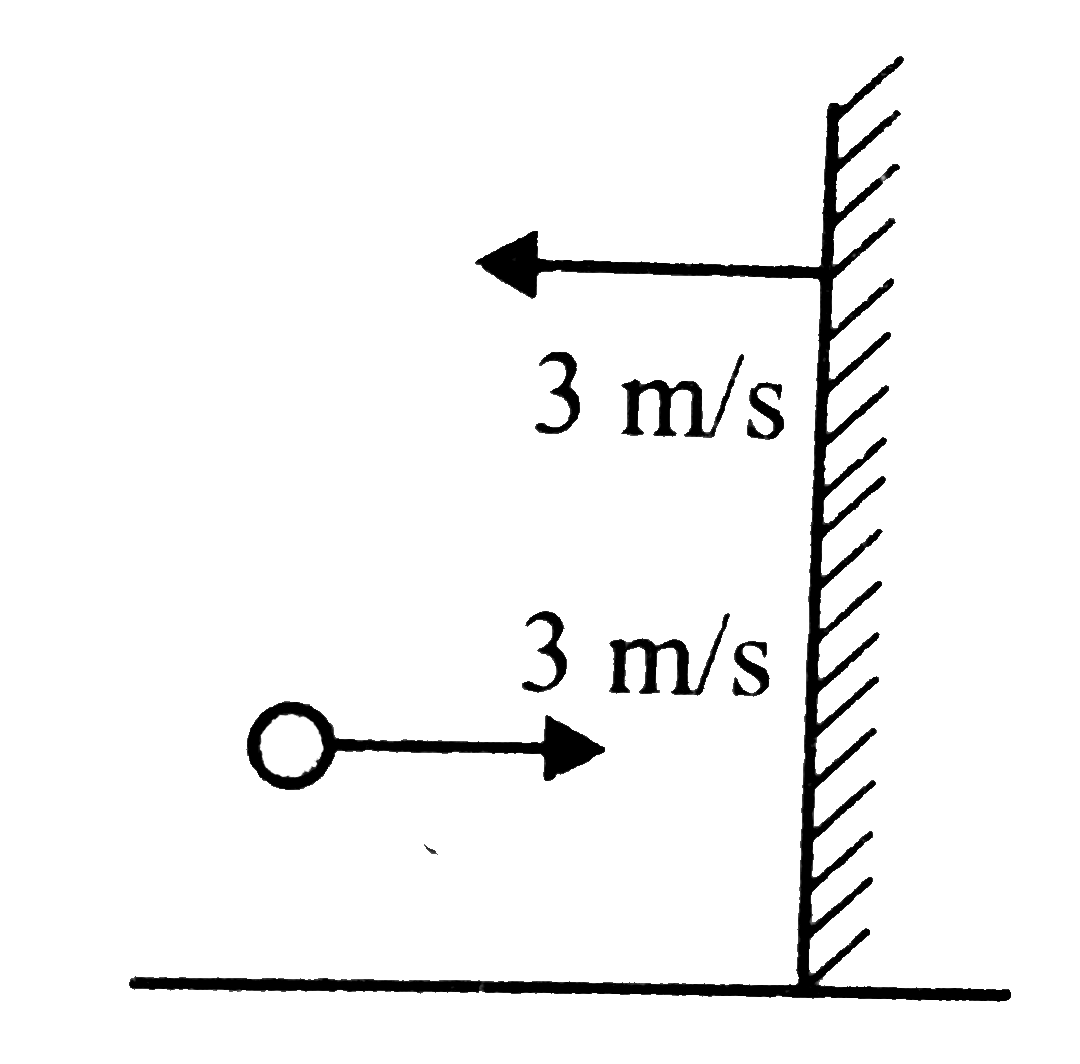
View Solution
Knowledge Check
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzeroA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
A2muBmuCzeroD−2muA ball of mass m strikes a rigid walJ with speed u and rebounds with the same speed. The impulse imparted to the ball by the wall is
 Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
Amu sin30∘tB2mu sin30∘tCmu cos30∘tD2mu cos30∘t
A 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
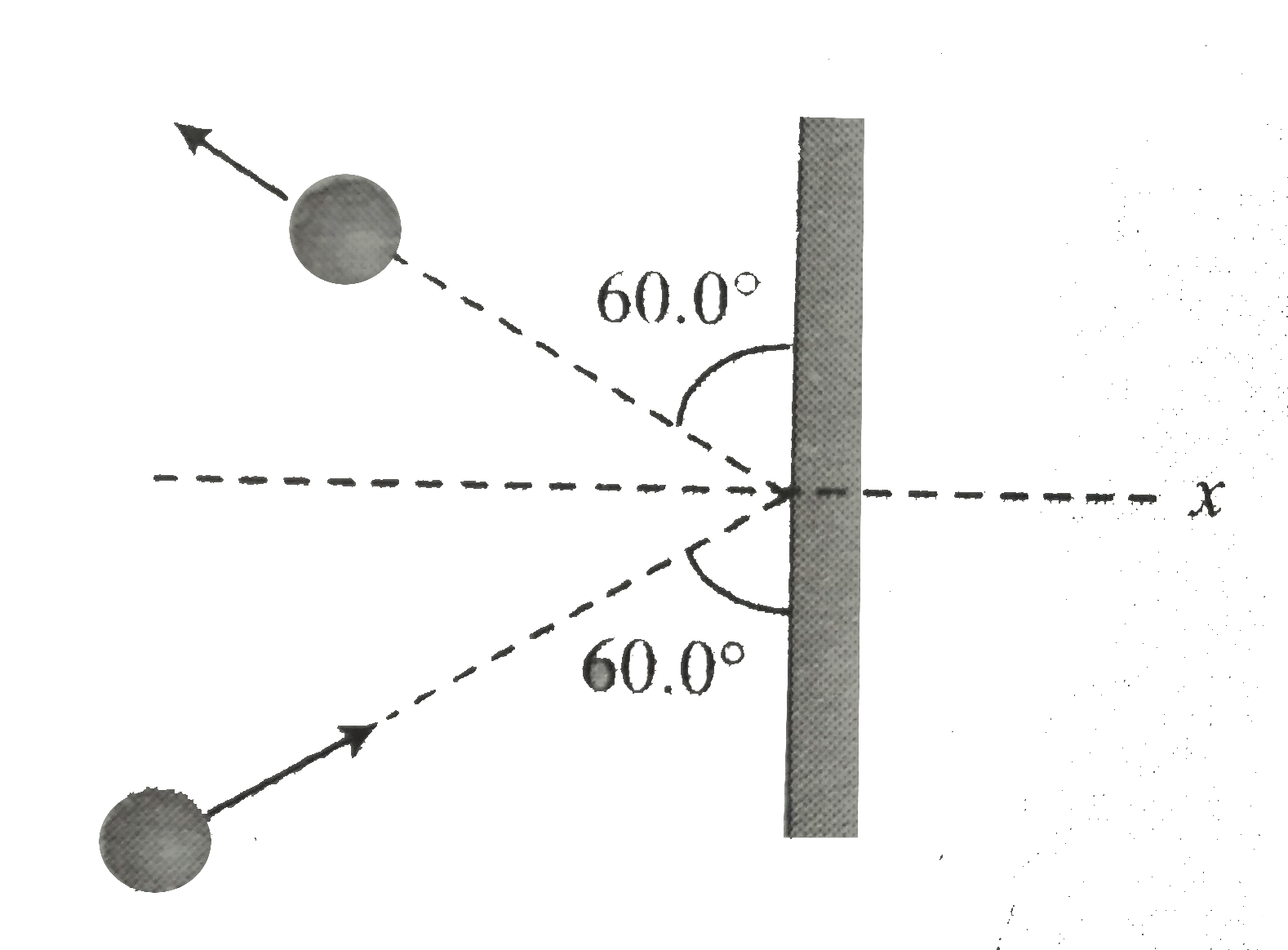
View SolutionTwo balls roll towards each other. The red ball has a mass kg 0.5 kg and a speed of 4 m/s just before impact. The green ball has a mass of 0.3 kg and a speed of 2m/s. after the head-on collision, the red ball continues forward with a speed of 2m/s. find the speed of the green ball after the collision. was the collision elastic?
View SolutionA massive vertical wall is approaching a man at a speed μ. When it is at a distance of 10m, the man throws a ball with speed 10 m/s at an angle of 37∘, which after having a completely elastic collision with the wall, reaches back directly into the hands of the man. The velocity of the wall is
View SolutionIf a ball strickes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionTwo balls of equal mass have a head on collision with speed 4ms−1 each travelling in opposite direction. If the coefficient's of resolution is 12, the speed of each ball after impact will be
View Solution
