A particle of mass m is projected towards a wall such that the angle of incidence is θ and the speed just before collision is u. Assuming that the wall is smooth and the collision is elastic, show that the ball rebounds at same angle.
The situation shown in figure. As the collision is elastic,thereis no loss of energy and hence speed of rebound is same.
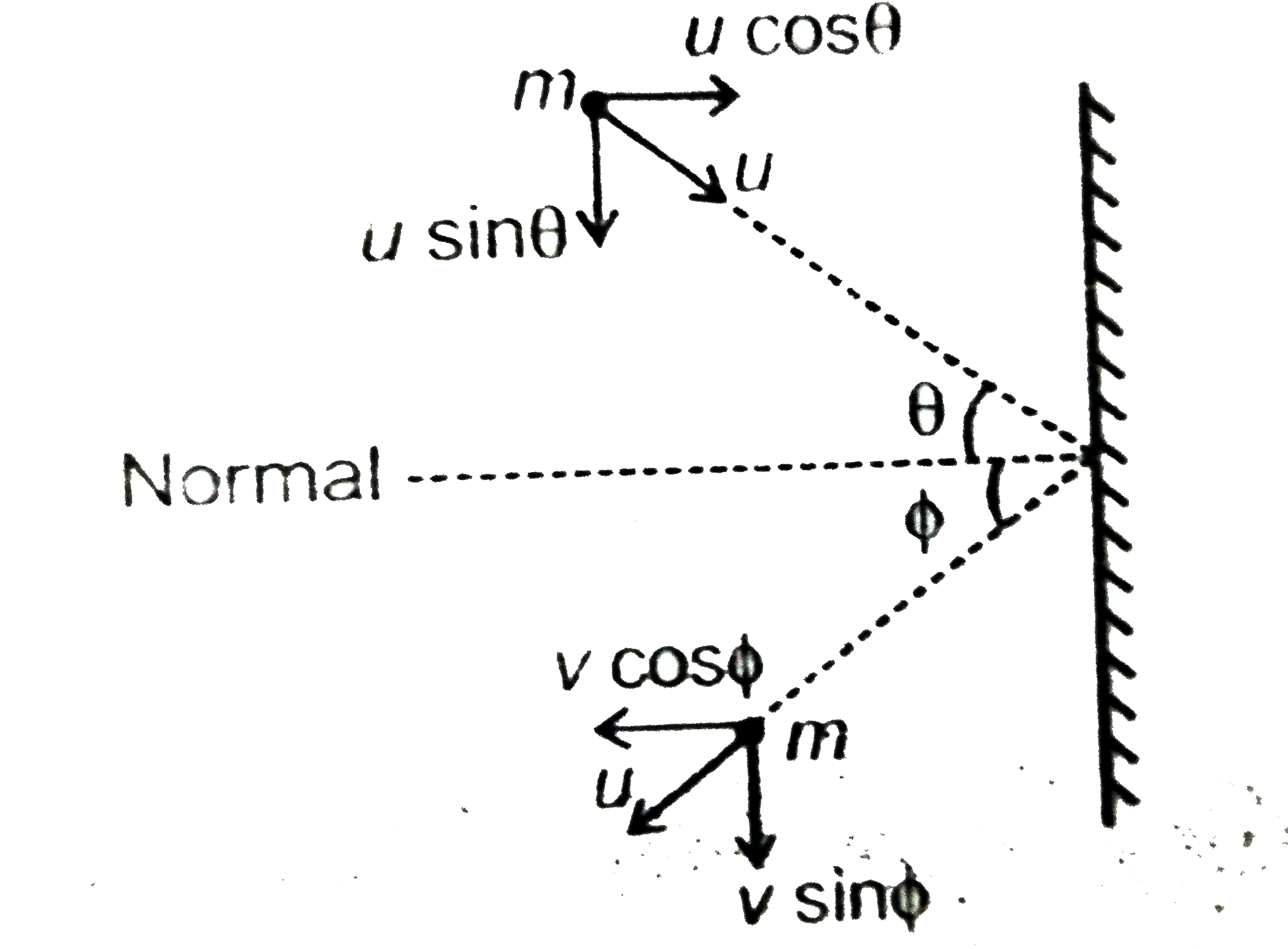
The contact forrce between thewall and ball is along the normal, as friction is absent. So the magnitude ofmomentum of ball along the wall must not change
Now,v=u (No loss of energy)
Also vsinϕ=usinθ(Noforce along the wall)
θ=ϕ
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF
95 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle is projected at an angle θ with an initial speed u.
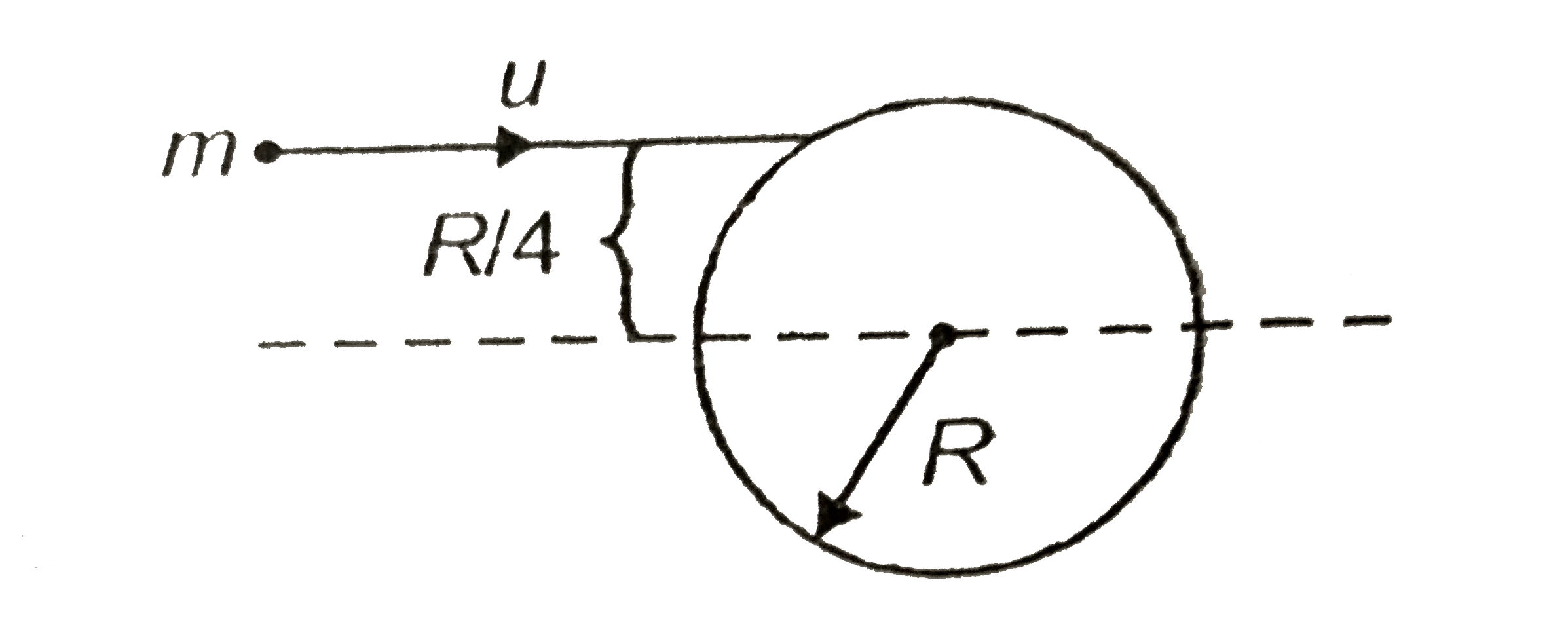
View SolutionA particle of mass m strikes a disc of radius R and mass m with a speed u as shown in the figure. What is the speed of the particle just after the collision if the collision is perfectly inelastic ?
View SolutionA ball of mass m approaches a heavy wall of mass M with speed 4 m/s along the normal to the wall. The speed of wall before collision is 1m/s towards the ball. The ball collides elastically with the wall. What can you say about the speed of the ball after collision? Will it be slightly less than or slightly higher than 6 m/s ?
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m strikes elastically on a wall with velocity v, at an angle of 60∘ from the wall then magnitude of change in momentum of ball along the wall is
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
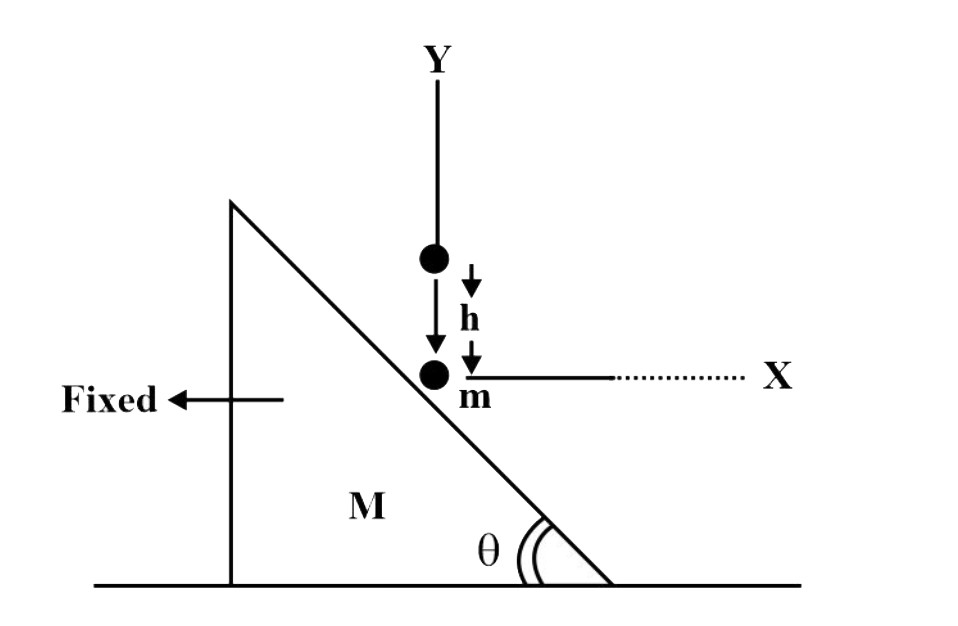
View SolutionA ball of mass m is dropped onto a smooth fixed wedge of inclination θ The collision is perfectly elastic . If after the collision, the x component of the velocity of the block is √2gh , then θ is
View SolutionA ball of mass m approaches a wall of mass M (M>>m), with speed 2 ms−1 along the normal to the wall. The speed of wall is 1 ms−1 towards the ball. The speed of the ball after an elastic collision with the wall is-
View SolutionA parallel beam of particles each of mass m moving with velocity v impinges on a wall at an angle θ to its normal. The number of particles per unit volume in the beam is n. If the collision of particles with the wall is elastic, then the pressure exerted by this beam on the wall is
View Solution
