In which o the following cases the centre of mass of a rod is certainly not at its centre?
the density cintinuously increase from left to right
the density con tinuously decreases from left to right
the density decreases from left to tight upto the center and then incrases
the density increases from left to right upto the centre and then decreases
To determine in which cases the center of mass of a rod is certainly not at its center, we need to analyze the conditions presented in the options.
1. Understanding Center of Mass: The center of mass of a uniform rod is located at its geometric center. However, if the mass distribution along the rod is not uniform, the center of mass will shift towards the denser region.
2. Analyzing the First Option:
- The first option states that the mass of the rod varies according to its length, with the mass increasing continuously from one end to the other.
- If the density increases from left to right, the center of mass will shift towards the right side of the rod, meaning it will not be at the center.
- Conclusion: This option is correct; the center of mass is not at the center.
3. Analyzing the Second Option:
- The second option indicates that the mass of the rod decreases as the length decreases, suggesting that the density decreases continuously from one end to the other.
- If the density decreases from left to right, the center of mass will shift towards the left side of the rod, again indicating that it will not be at the center.
- Conclusion: This option is also correct; the center of mass is not at the center.
4. Final Conclusion: Both the first and second options indicate scenarios where the center of mass of the rod is not located at its geometric center.
Summary of the Answer:
The center of mass of the rod is certainly not at its center in both the first and second cases.
- The first option states that the mass of the rod varies according to its length, with the mass increasing continuously from one end to the other.
- If the density increases from left to right, the center of mass will shift towards the right side of the rod, meaning it will not be at the center.
- Conclusion: This option is correct; the center of mass is not at the center.
- The second option indicates that the mass of the rod decreases as the length decreases, suggesting that the density decreases continuously from one end to the other.
- If the density decreases from left to right, the center of mass will shift towards the left side of the rod, again indicating that it will not be at the center.
- Conclusion: This option is also correct; the center of mass is not at the center.
The center of mass of the rod is certainly not at its center in both the first and second cases.
Similar Questions
In which of the following cases the centre of mass of a rod is certainly not at its centre?
View Solutionin which fo the following cases the centre of mass of a rod is certainly not at its centre?
(A) The density continuously increases from left ot right
(B) The density continuously decreases from left to right
(C) The density decreases from left to right up to the centre and then increases
(D) The density increases from left to right up to the centre and then decreases
Select correct alternative.
View Solution
Knowledge Check
For which of the following does the centre of mass lie outside the body ?
AA pencilBA shotputCA diceDA bangle
For which of the following does the centre of mass lie outside the body ?
View SolutionFor which of the following does the centre of mass lie outside the body ?
View SolutionWhich of the following is the centre of intelligence ?
View SolutionFor a uniform ring of mass M and radius R at its centre
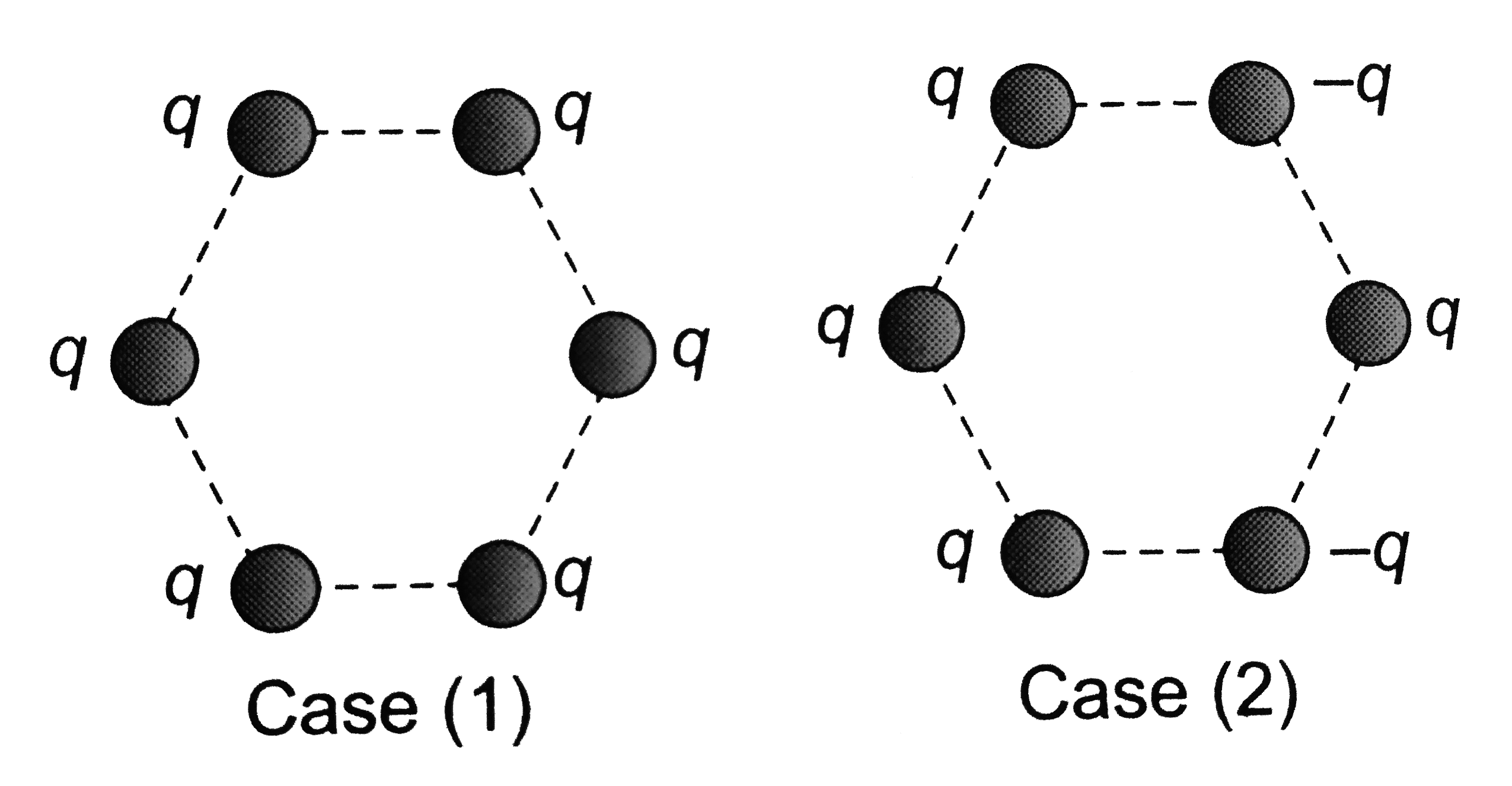
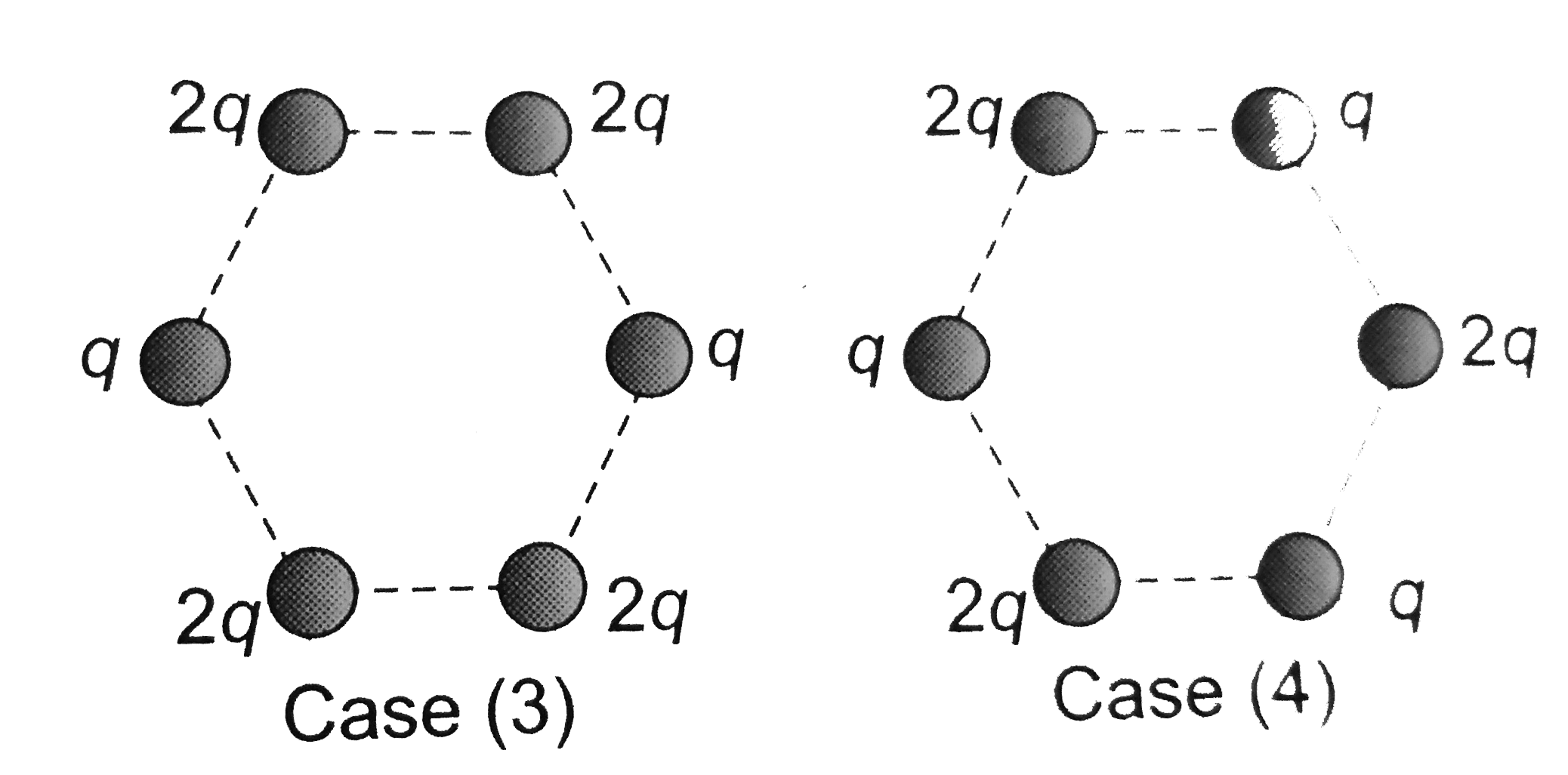
View SolutionFigure below show regular hexagons with charges at the vertices. In which of the following cases the electric field at the centre is not zero
View SolutionThe distance of the centre of mass of T-shaped uniform plate from O is :
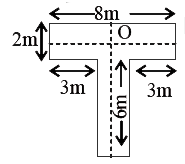
View SolutionTwo identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as shown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View Solution
