Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
If both the particles have the same value of coefficient of friction μ=0.2. The centre of mass will stop at time t= ..........s :-
1.5
4.5
3.0
2.0
To solve the problem, we need to determine the time at which the center of mass of the two particles comes to rest due to friction. Let's break down the solution step by step.
Step 1: Identify the initial conditions
- Mass of particle 1 (m1) = 1 kg, initial velocity (u1) = 3 m/s, initial position (x1) = (3 m, 0).
- Mass of particle 2 (m2) = 2 kg, initial velocity (u2) = 6 m/s, initial position (x2) = (0, 9 m).
- Coefficient of friction (μ) = 0.2.
Step 2: Calculate the normal forces
For both particles, the normal force (N) can be calculated using the formula:
N=m⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
- For particle 1:
N1=m1⋅g=1⋅10=10N
- For particle 2:
N2=m2⋅g=2⋅10=20N
Step 3: Calculate the frictional forces
The frictional force (F_f) acting on each particle can be calculated using:
Ff=μ⋅N
- For particle 1:
Ff1=μ⋅N1=0.2⋅10=2N
- For particle 2:
Ff2=μ⋅N2=0.2⋅20=4N
Step 4: Calculate the retardation (deceleration) for each particle
Using Newton's second law, the retardation (a) can be calculated as:
a=Ffm
- For particle 1:
a1=Ff1m1=21=2m/s2
- For particle 2:
a2=Ff2m2=42=2m/s2
Step 5: Calculate the time taken for each particle to come to rest
Using the equation of motion:
v=u+at
where v is the final velocity (0 when the particle comes to rest), u is the initial velocity, and a is the retardation.
- For particle 1:
0=3−2t
2t=3
t1=32=1.5s
- For particle 2:
0=6−2t
2t=6
t2=62=3s
Step 6: Determine the time at which the center of mass stops
The center of mass will stop moving when both particles have come to rest. Since particle 1 stops at t1=1.5s and particle 2 stops at t2=3s, the center of mass will come to rest at:
tCM=t2=3s
Final Answer
The center of mass will stop at time t=3s.
---
- Mass of particle 1 (m1) = 1 kg, initial velocity (u1) = 3 m/s, initial position (x1) = (3 m, 0).
- Mass of particle 2 (m2) = 2 kg, initial velocity (u2) = 6 m/s, initial position (x2) = (0, 9 m).
- Coefficient of friction (μ) = 0.2.
For both particles, the normal force (N) can be calculated using the formula:
N=m⋅g
where g is the acceleration due to gravity (approximately 10m/s2).
N1=m1⋅g=1⋅10=10N
N2=m2⋅g=2⋅10=20N
The frictional force (F_f) acting on each particle can be calculated using:
Ff=μ⋅N
Ff1=μ⋅N1=0.2⋅10=2N
Ff2=μ⋅N2=0.2⋅20=4N
Using Newton's second law, the retardation (a) can be calculated as:
a=Ffm
a1=Ff1m1=21=2m/s2
a2=Ff2m2=42=2m/s2
Using the equation of motion:
v=u+at
where v is the final velocity (0 when the particle comes to rest), u is the initial velocity, and a is the retardation.
0=3−2t
2t=3
t1=32=1.5s
0=6−2t
2t=6
t2=62=3s
The center of mass will stop moving when both particles have come to rest. Since particle 1 stops at t1=1.5s and particle 2 stops at t2=3s, the center of mass will come to rest at:
tCM=t2=3s
The center of mass will stop at time t=3s.
Similar Questions
Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line for which equation is :
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is rough for question, if cofficient of friction is 0.2 in both axis)
Co-ordinates of center of mass where it will stop finally are :-
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
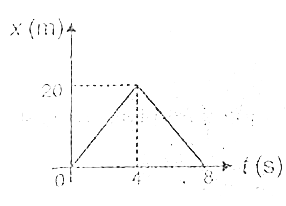
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View SolutionA body of mass m=3.513kg is moving along the x-axis with a speed of 5.00ms−1. The magnetude of its momentum is recorded as
View SolutionA body of mass m=3.513kg is moving along the x-axis with a speed of 5.00ms−1. The magnetude of its momentum is recorded as
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionA particle of mass 1 kg is projected upwards with velocity 60 m/s. Another particle of mass 2 kg is just deopper from a certain height. After 2 kg is just of the particles have colliided with ground, match the following [ Take g= 10 m/s2]
View Solution
