The radii of the two columns is U-tube are r1 and r2(r2>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
ρghr1r22(r2−r1)
ρgh(r2−r1)2r1r2
2(r2−r1)ρghr1r2
ρgh2(r2−r1)
The correct Answer is:A
To find the surface tension of the liquid in the U-tube, we can follow these steps:
Step 1: Understand the Problem
We have a U-tube with two arms of different radii, r1 and r2 (where r2>r1). A liquid of density ρ is filled in the U-tube, and the angle of contact is 0∘. The height difference between the two arms is h.
Step 2: Use the Formula for Height due to Surface Tension
The height to which the liquid rises in each arm due to surface tension can be expressed as:
h1=2Tcosθρgr1
h2=2Tcosθρgr2
Since the angle of contact θ=0∘, we have cos0∘=1. Therefore, the equations simplify to:
h1=2Tρgr1
h2=2Tρgr2
Step 3: Relate the Heights to the Given Height Difference
The total height difference h between the two arms can be expressed as:
h=h1−h2
Substituting the expressions for h1 and h2:
h=2Tρgr1−2Tρgr2
Step 4: Factor Out Common Terms
Factoring out the common terms from the right side:
h=2Tρg(1r1−1r2)
Step 5: Solve for Surface Tension T
Rearranging the equation to solve for T:
T=hρg2⎛⎝11r1−1r2⎞⎠
This can be further simplified:
T=hρgr1r22(r2−r1)
Final Answer
Thus, the surface tension T of the liquid is given by:
T=ρghr1r22(r2−r1)
We have a U-tube with two arms of different radii, r1 and r2 (where r2>r1). A liquid of density ρ is filled in the U-tube, and the angle of contact is 0∘. The height difference between the two arms is h.
The height to which the liquid rises in each arm due to surface tension can be expressed as:
h1=2Tcosθρgr1
h2=2Tcosθρgr2
Since the angle of contact θ=0∘, we have cos0∘=1. Therefore, the equations simplify to:
h1=2Tρgr1
h2=2Tρgr2
The total height difference h between the two arms can be expressed as:
h=h1−h2
Substituting the expressions for h1 and h2:
h=2Tρgr1−2Tρgr2
Factoring out the common terms from the right side:
h=2Tρg(1r1−1r2)
Rearranging the equation to solve for T:
T=hρg2⎛⎝11r1−1r2⎞⎠
This can be further simplified:
T=hρgr1r22(r2−r1)
Thus, the surface tension T of the liquid is given by:
T=ρghr1r22(r2−r1)
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)
View SolutionIn a U-tube the radii of two columns are respectively r1andr2 and if a liquid of density d filled in it has level difference of h then the surface tension of the liquid is -

View Solution
Knowledge Check
The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)Aρghr1r22(r2−r1)Bρgh(r1−r2)2r1r2C2(r2−r1)ρghr1r2Dρgh2(r2−r1)The radii of the two columne is U-tube are r1 and r2(>r1). When a liquid of density ρ (angle of contact is 0∘)) is filled in it, the level different of liquid in two arms is h. The surface tension of liquid is
(g= acceleration due to gravity)Aρghr1r22(r2−r1)Bρgh(r2−r1)2r1r2C2(r2−r1)ρghr1r2Dρgh2(r2−r1)
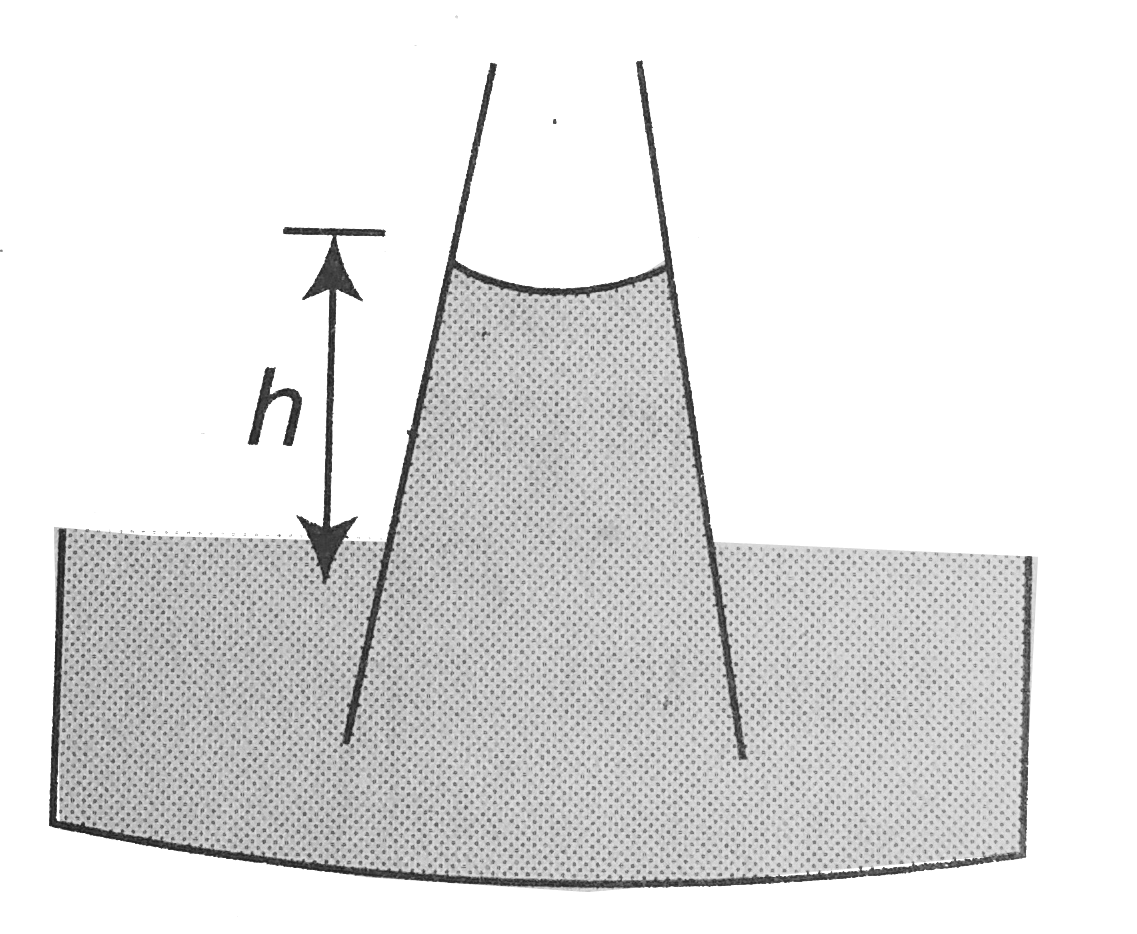
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View SolutionA capillary tube of radius r is lowered into a liquid of surface tension T and density ρ. Given angle of contact =0∘.
What is the potential energy acquired by the liquid in the capillary?
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
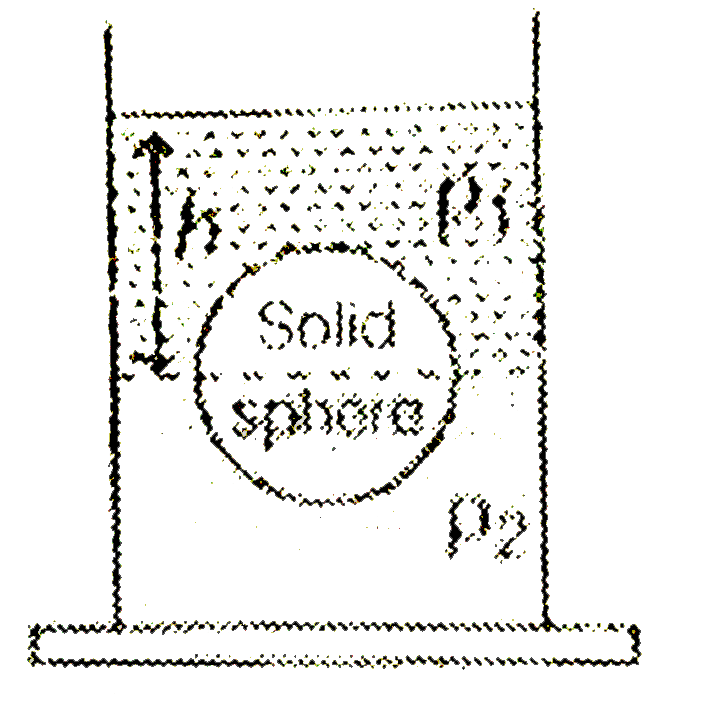
View SolutionTwo holes are made at depths h and 2h from the top. A liquid of density ρ and height h is filled over another liquid of density 2ρ. Speeds of liquid ejecting from two holes are say v1 and v2.

If density of lower liquid is increased
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionA liquid of density ρ and surface tension σ rises in a capillary tube of diameter d. Angle of contact between the tube and liquid is zero. The weight of the liquid in the capillary tube is:
View Solution
