The absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
ρgh
Pa+ρgh
Pa−ρgh
Pa2ρgh
The correct Answer is:B
To find the absolute pressure at a depth h below the surface of a liquid with density ρ, we can follow these steps:
Step 1: Understand the Concept of Pressure in Fluids
Pressure in a fluid increases with depth due to the weight of the fluid above. The pressure at a certain depth is the sum of the atmospheric pressure and the pressure due to the column of liquid above that point.
Step 2: Identify the Variables
- Let Pa be the atmospheric pressure at the surface of the liquid.
- Let ρ be the density of the liquid.
- Let g be the acceleration due to gravity.
- Let h be the depth below the surface of the liquid.
Step 3: Calculate the Pressure Due to the Liquid Column
The pressure exerted by a column of liquid of height h is given by the formula:
Pliquid=ρgh
This represents the additional pressure due to the weight of the liquid above the point at depth h.
Step 4: Calculate the Absolute Pressure at Depth h
The absolute pressure at depth h is the sum of the atmospheric pressure and the pressure due to the liquid column:
P=Pa+Pliquid
Substituting the expression for Pliquid:
P=Pa+ρgh
Final Answer
Thus, the absolute pressure at a depth h below the surface of a liquid of density ρ is:
P=Pa+ρgh
---
Pressure in a fluid increases with depth due to the weight of the fluid above. The pressure at a certain depth is the sum of the atmospheric pressure and the pressure due to the column of liquid above that point.
- Let Pa be the atmospheric pressure at the surface of the liquid.
- Let ρ be the density of the liquid.
- Let g be the acceleration due to gravity.
- Let h be the depth below the surface of the liquid.
The pressure exerted by a column of liquid of height h is given by the formula:
Pliquid=ρgh
This represents the additional pressure due to the weight of the liquid above the point at depth h.
The absolute pressure at depth h is the sum of the atmospheric pressure and the pressure due to the liquid column:
P=Pa+Pliquid
Substituting the expression for Pliquid:
P=Pa+ρgh
Thus, the absolute pressure at a depth h below the surface of a liquid of density ρ is:
P=Pa+ρgh
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - C
15 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - TRY YOURSELF
41 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
What is the absolute pressure on a swimmer 10m below the surface of a lake? Take atmospheric pressure 1×105N/m2
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
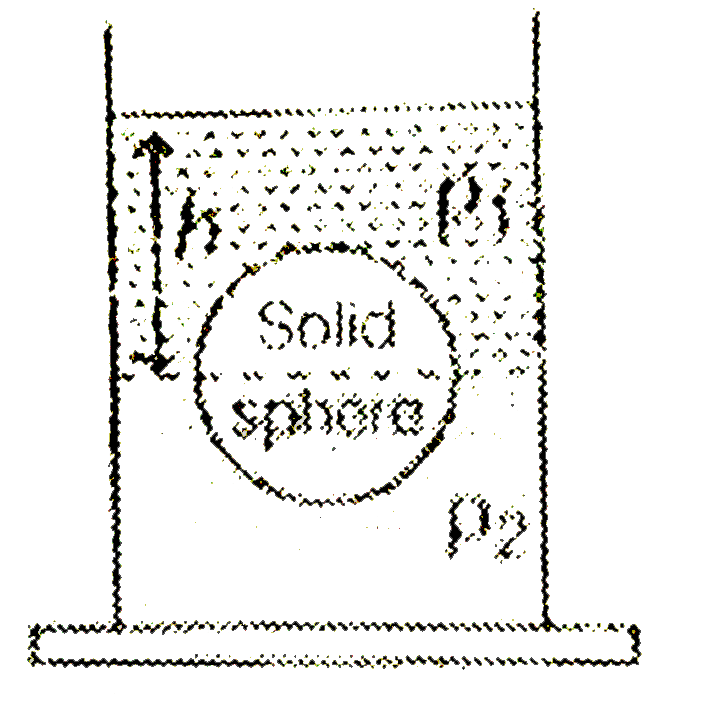
View Solution
Knowledge Check
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depthThe pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
The acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionFind the total pressure inside a sperical air bubble of radius 0.2 mm. The bubble is at a depth 5 cm below the surface of a liquid of density 2×103 kg m−3 and surface tension 0.082 N m−1. (Given : atmospheric pressure = 1.01 ×105Nm−2)
Hint : Pi=Po+2SR
Po = atmospheric pressure + gauge pressure of liquid column.
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View SolutionAn air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectively . the pressure inside the bubble will be :
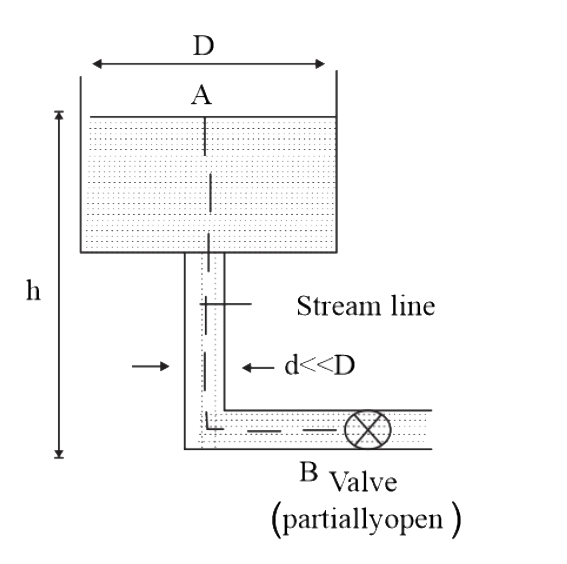
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
View SolutionThere is an air bubble of radius 1.0mm in a liquid of surface tension 0.075Nm−1 and density 103kgm−3. The bubble is at a depth of 10.0cm below the free surface of a liquid. By what amount is the pressure inside the bubble greater than the atmospheric pressure?
View Solution
