Two spheres of volume 250 cc each but of relative densities 0.8 and 1.2 are connected by a string and the combination is immersed in a liquid. Find the tension T in the string.
The correct Answer is:B
To find the tension T in the string connecting the two spheres, we can follow these steps:
Step 1: Understand the Problem
We have two spheres with volumes of 250 cc each, having relative densities of 0.8 and 1.2. We need to find the tension in the string when they are immersed in a liquid.
Step 2: Convert Volume to Cubic Meters
The volume of each sphere is given as 250 cc. We convert this to cubic meters:
V=250cc=250×10−6m3
Step 3: Calculate the Densities of the Spheres
Using the relative densities, we can find the actual densities of the spheres:
- Density of Sphere 1 (ρ1):
ρ1=0.8×ρw=0.8×1000kg/m3=800kg/m3
- Density of Sphere 2 (ρ2):
ρ2=1.2×ρw=1.2×1000kg/m3=1200kg/m3
Step 4: Calculate the Weight of Each Sphere
The weight of each sphere can be calculated using the formula W=mg:
- Weight of Sphere 1 (W1):
W1=m1g=ρ1Vg=800×250×10−6×10=2N
- Weight of Sphere 2 (W2):
W2=m2g=ρ2Vg=1200×250×10−6×10=3N
Step 5: Calculate the Buoyant Force on Each Sphere
The buoyant force (FB) acting on each sphere is equal to the weight of the liquid displaced, which is the same for both since they have the same volume:
FB=ρliquidVg
Assuming the liquid is water (ρliquid=1000kg/m3):
FB=1000×250×10−6×10=2.5N
Step 6: Apply Newton's Second Law to Each Sphere
For Sphere 1:
FB−T−W1=0⟹2.5−T−2=0⟹T=0.5N
For Sphere 2:
T+FB−W2=0⟹T+2.5−3=0⟹T=0.5N
Step 7: Conclusion
The tension T in the string connecting the two spheres is:
T=0.5N
Final Answer
The tension in the string is 0.5N.
We have two spheres with volumes of 250 cc each, having relative densities of 0.8 and 1.2. We need to find the tension in the string when they are immersed in a liquid.
The volume of each sphere is given as 250 cc. We convert this to cubic meters:
V=250cc=250×10−6m3
Using the relative densities, we can find the actual densities of the spheres:
- Density of Sphere 1 (ρ1):
ρ1=0.8×ρw=0.8×1000kg/m3=800kg/m3
- Density of Sphere 2 (ρ2):
ρ2=1.2×ρw=1.2×1000kg/m3=1200kg/m3
The weight of each sphere can be calculated using the formula W=mg:
- Weight of Sphere 1 (W1):
W1=m1g=ρ1Vg=800×250×10−6×10=2N
- Weight of Sphere 2 (W2):
W2=m2g=ρ2Vg=1200×250×10−6×10=3N
The buoyant force (FB) acting on each sphere is equal to the weight of the liquid displaced, which is the same for both since they have the same volume:
FB=ρliquidVg
Assuming the liquid is water (ρliquid=1000kg/m3):
FB=1000×250×10−6×10=2.5N
For Sphere 1:
FB−T−W1=0⟹2.5−T−2=0⟹T=0.5N
T+FB−W2=0⟹T+2.5−3=0⟹T=0.5N
The tension T in the string connecting the two spheres is:
T=0.5N
The tension in the string is 0.5N.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Two solid spheres A and B of equal volumes but of different densities dAanddB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if

View SolutionA silver block of mass 3.1 kg is connected to a string and is then immersed in a liquid of relative density 0.82 . Find the tension in the string , if relative density of silver is 10.5
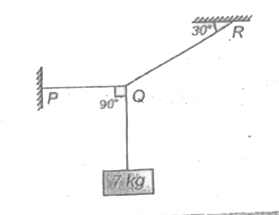
View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)

View SolutionTwo particles of masses m1andm2 are connected to a string and the system is rotated in a horizontal plane with 'P' as center. The ratio of tension in the two parts of string is

View SolutionFind the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]

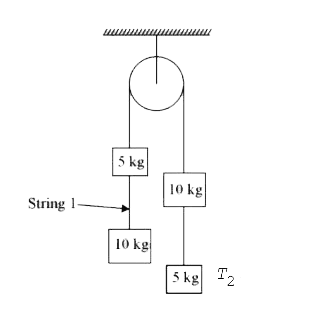
View SolutionFind the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
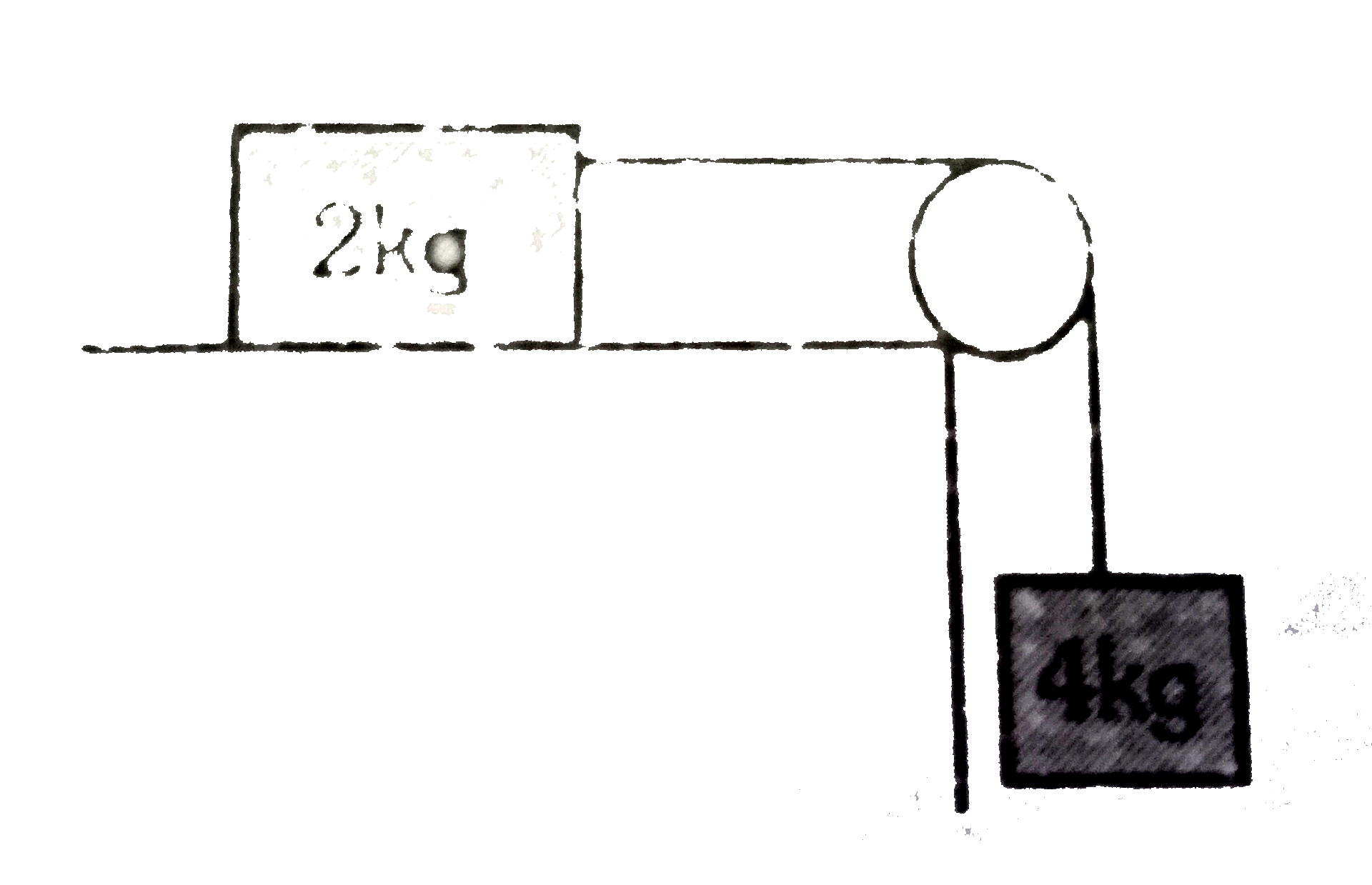
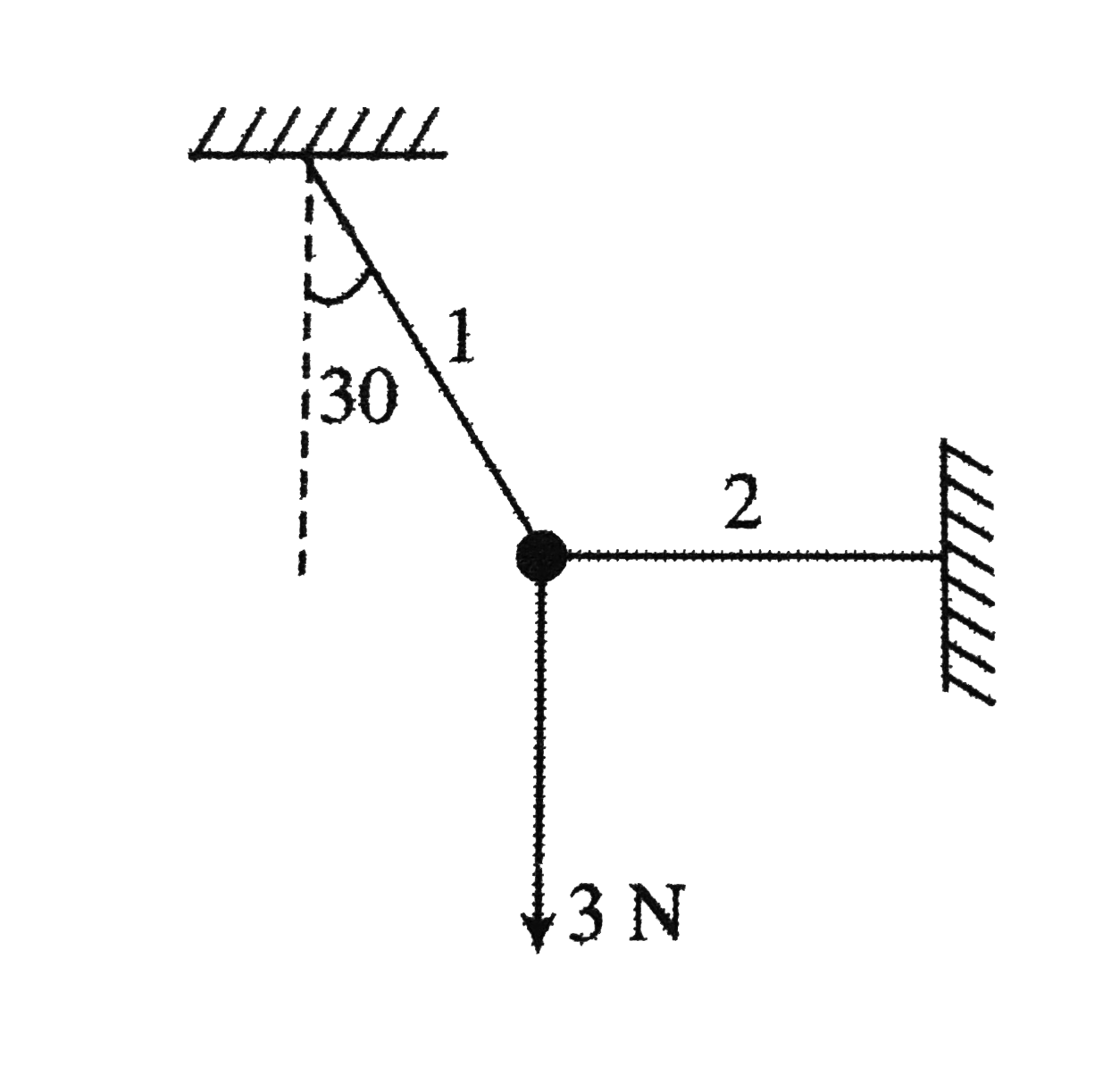
View SolutionA bob of weight 3N is in equilibrium under the action of two string 1 and 2 (figure) . Find the tension forces in the string.
View SolutionIn the arrangement as shown, tension T2 is (g=10m/s2)
View Solution
