A cylindrical vessel of area of cross-section A is filled with water to a height H. It has capillary tube of length l and radius r fitted horizontally at its bottom. If the coeffiecient of viscosity of water is , then time required in which level will fall to a height is (density of water is )
The correct Answer is:C
To solve the problem step by step, we will use the principles of fluid dynamics and the properties of viscosity.
Step 1: Understand the Setup
We have a cylindrical vessel filled with water to a height H. A capillary tube of length l and radius r is fitted horizontally at the bottom of the vessel. We need to find the time required for the water level to fall from H to H2.
Step 2: Define Variables
- Let A be the area of the cross-section of the cylindrical vessel.
- Let η be the coefficient of viscosity of water.
- Let ρ be the density of water.
- Let g be the acceleration due to gravity.
- Let h be the height of the water level at any time t.
Step 3: Rate of Flow from the Vessel
The rate of flow of water out of the vessel can be expressed as:
V=−Adhdt
This equation indicates that as the height h decreases, the volume flow rate V is negative.
Step 4: Apply Poiseuille's Law
According to Poiseuille's equation, the flow rate V through the capillary tube can be expressed as:
V=πr48ηlΔP
Where ΔP is the pressure difference driving the flow. The pressure difference can be given by:
ΔP=ρgh
Thus, we can rewrite the flow rate as:
V=πr48ηlρgh
Step 5: Set the Two Expressions for Flow Rate Equal
Equating the two expressions for flow rate, we have:
−Adhdt=πr48ηlρgh
Step 6: Rearranging the Equation
Rearranging gives:
dhh=−πρgr48ηlAdt
Step 7: Integrate Both Sides
Integrating both sides, we have:
∫dhh=−πρgr48ηlA∫dt
The limits for h will change from H to H2 and for t from 0 to T:
(lnh)H2H=−πρgr48ηlAT
Step 8: Evaluate the Integral
Evaluating the left side:
ln(H2)−ln(H)=ln(H/2H)=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−πρgr48ηlAT
Step 9: Solve for Time T
Rearranging gives:
T=8ηlAln(2)πρgr4
Final Answer
The time required for the water level to fall from H to H2 is:
T=8ηlAln(2)πρgr4
We have a cylindrical vessel filled with water to a height H. A capillary tube of length l and radius r is fitted horizontally at the bottom of the vessel. We need to find the time required for the water level to fall from H to H2.
- Let A be the area of the cross-section of the cylindrical vessel.
- Let η be the coefficient of viscosity of water.
- Let ρ be the density of water.
- Let g be the acceleration due to gravity.
- Let h be the height of the water level at any time t.
The rate of flow of water out of the vessel can be expressed as:
V=−Adhdt
This equation indicates that as the height h decreases, the volume flow rate V is negative.
According to Poiseuille's equation, the flow rate V through the capillary tube can be expressed as:
V=πr48ηlΔP
Where ΔP is the pressure difference driving the flow. The pressure difference can be given by:
ΔP=ρgh
Thus, we can rewrite the flow rate as:
V=πr48ηlρgh
Equating the two expressions for flow rate, we have:
−Adhdt=πr48ηlρgh
Rearranging gives:
dhh=−πρgr48ηlAdt
Integrating both sides, we have:
∫dhh=−πρgr48ηlA∫dt
The limits for h will change from H to H2 and for t from 0 to T:
(lnh)H2H=−πρgr48ηlAT
Evaluating the left side:
ln(H2)−ln(H)=ln(H/2H)=ln(12)=−ln(2)
Thus, we have:
−ln(2)=−πρgr48ηlAT
Rearranging gives:
T=8ηlAln(2)πρgr4
The time required for the water level to fall from H to H2 is:
T=8ηlAln(2)πρgr4
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View SolutionWater rises to a height of 30 mm in a capillary tube. If the radius of the capillary tube is made 3/4 of its previous value. The height to which the water will rise in the tube is
View SolutionA cylindrical container of cross-section area, A is filled up with water upto height 'h' Water may exit through a tap of cross sectional area 'a' in the bottom of container. Find out

(a) Velocity of water just after opening of tap.
(b) The area of cross-section of water stream coming out of tape at depth h0 below tap in terms of 'a' just after opening of tap.
(c) Time in which conainer becomes empty.
(Given : (aA)1/2=0.22,h=20cm,h0=20cm
View SolutionWater rises to height h in capillary tube. If the length of capillary tube above the surface of water is made less than h then
View SolutionWater rises to a height h when a capillary of radius r is dipped in water. For another capillary of radius 2r dipped in water, it rises to the height
View SolutionA cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the time required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View SolutionWater rises to a height of 10cm in a glass capillary tube. If the area of cross section of the tube is reduced to one fourth of the former value what is the height of water rise now?
View SolutionA cylindrical vessel of 90cm height is kept filled up to the brim. It has four holes 1,2,3 and 4 which are, respectively, at heights of 20cm,30cm,40cm and 50cm from the horizontal floor PQ. The water falling at the maximum horizontal distance from the vessel comes from

View SolutionTwo cylindrical vessels, each having length 10m and area of cross-sectional area of 1m2, are filled with water and rotated with angular speed ω=20rad/s. Then, which of the following statement is correct ?
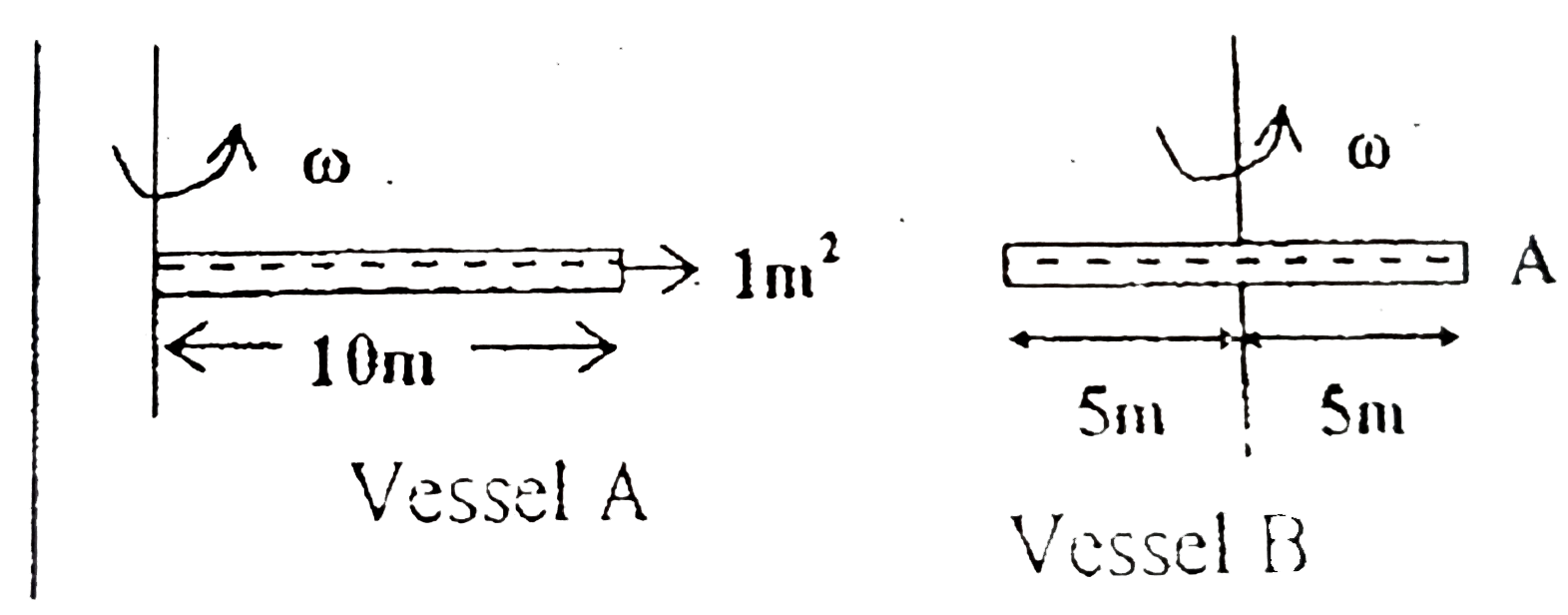
View Solution
