Question

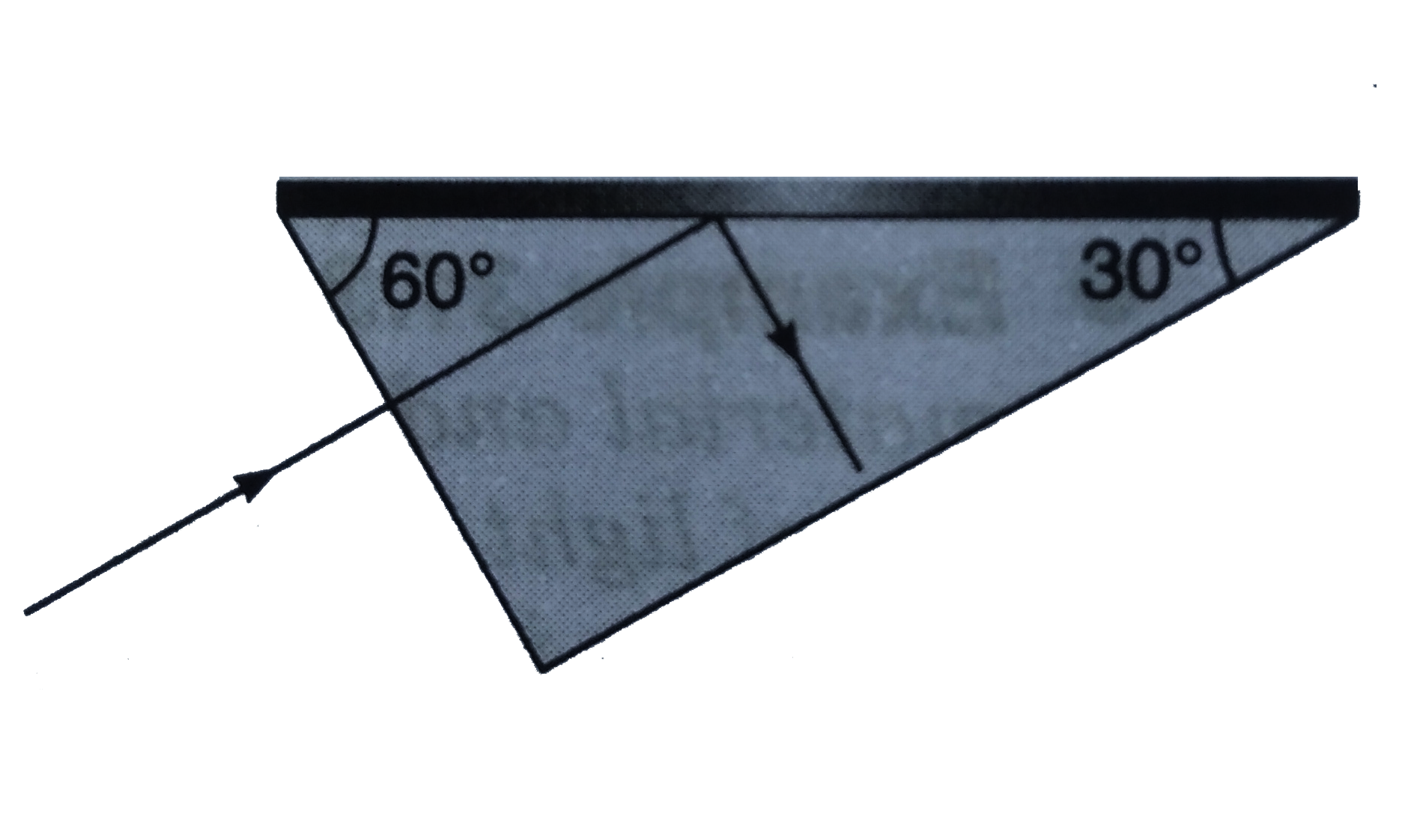
The refractive index of a prism is 2. this prism can have a maximum refracting angle of

Options

A. `90^(@)`
B. `60^(@)`
C. `45^(@)`
D. `30^(@)`

Answer

B

Explanation

To find the maximum refracting angle of a prism with a refractive index of 2, we can follow these steps:

Step 1: Understand the relationship between the refractive index and the critical angle
The critical angle (θc) for a prism can be determined using the formula:
\( \sin(\theta_c) = \frac{1}{\mu} \)
where \( \mu \) is the refractive index of the prism.

Step 2: Substitute the given refractive index
Given that the refractive index \( \mu = 2 \), we can substitute this value into the formula:
\( \sin(\theta_c) = \frac{1}{2} \)

Step 3: Calculate the critical angle
To find the critical angle, we take the inverse sine:
\( \theta_c = \sin^{-1}\left(\frac{1}{2}\right) \)
This gives us:
\( \theta_c = 30^\circ \)

Step 4: Relate the critical angle to the maximum refracting angle
For a prism, the maximum refracting angle \( A \) must be such that the angle of incidence at the first surface is less than or equal to the critical angle. The relationship between the angles is given by:
\( A = r_1 + r_2 \)
where \( r_1 \) and \( r_2 \) are the angles of refraction at the two faces of the prism.

Step 5: Determine the maximum value for angle A
Since the maximum angle of incidence at the first face cannot exceed the critical angle, we have:
\( A \leq 2 \times \theta_c \)
Thus, substituting the critical angle:
\( A \leq 2 \times 30^\circ = 60^\circ \)

Conclusion
Therefore, the maximum refracting angle \( A \) of the prism can be:
\( \boxed{60^\circ} \)