In displacement method distance of object from convex lens of focal length 20 cm in one position 60 cm. Then
in the other position distance of object from convex lens will be 30 cm
distance between object and screen is 90 cm
Both (a) and (b) are correct
Both (a) and (b) are wrong
The correct Answer is:C
To solve the problem using the displacement method for a convex lens, we will follow these steps:
Step 1: Identify the given data
- Focal length of the convex lens (f) = 20 cm
- Object distance in the first position (u₁) = -60 cm (the negative sign indicates that the object is on the opposite side of the light direction)
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
where:
- f = focal length
- v = image distance
- u = object distance
Substituting the known values into the lens formula:
120=1v−1−60
This simplifies to:
120=1v+160
Step 3: Solve for v
Rearranging the equation gives:
1v=120−160
To solve this, find a common denominator (which is 60):
120=360
So:
1v=360−160=260=130
Thus, we find:
v=30 cm
Step 4: Calculate the distance between the object and the screen
The distance between the object and the screen (D) is given by:
D=|u|+|v|=60+30=90 cm
Step 5: Determine the other position of the object
Let the object distance in the second position be u2. The image distance in this case will be:
v2=D−u2=90−u2
Using the lens formula again:
1f=1v2−1u2
Substituting v2:
120=190−u2−1u2
Step 6: Solve for u₂
Rearranging gives:
120=u2−(90−u2)u2(90−u2)
This simplifies to:
120=2u2−90u2(90−u2)
Cross-multiplying leads to:
u2(90−u2)=20(2u2−90)
Expanding both sides:
90u2−u22=40u2−1800
Rearranging gives:
u22−50u2+1800=0
Step 7: Solve the quadratic equation
Using the quadratic formula:
u2=−b±√b2−4ac2a
where a=1,b=−50,c=1800:
u2=50±√(−50)2−4⋅1⋅18002⋅1
Calculating the discriminant:
u2=50±√2500−72002
This gives:
u2=50±√25002=50±302
The two solutions are:
u2=802=40andu2=202=10
However, since we are looking for the second position where the object distance is 30 cm, we find:
u2=30 cm
Final Answer
Both statements in the options are correct:
- The distance of the object from the convex lens in the other position is 30 cm.
- The distance between the object and the screen is 90 cm.
- Focal length of the convex lens (f) = 20 cm
- Object distance in the first position (u₁) = -60 cm (the negative sign indicates that the object is on the opposite side of the light direction)
The lens formula is given by:
1f=1v−1u
where:
- f = focal length
- v = image distance
- u = object distance
120=1v−1−60
This simplifies to:
120=1v+160
Rearranging the equation gives:
1v=120−160
To solve this, find a common denominator (which is 60):
120=360
So:
1v=360−160=260=130
Thus, we find:
v=30 cm
The distance between the object and the screen (D) is given by:
D=|u|+|v|=60+30=90 cm
Let the object distance in the second position be u2. The image distance in this case will be:
v2=D−u2=90−u2
1f=1v2−1u2
Substituting v2:
120=190−u2−1u2
Rearranging gives:
120=u2−(90−u2)u2(90−u2)
This simplifies to:
120=2u2−90u2(90−u2)
Cross-multiplying leads to:
u2(90−u2)=20(2u2−90)
Expanding both sides:
90u2−u22=40u2−1800
Rearranging gives:
u22−50u2+1800=0
Using the quadratic formula:
u2=−b±√b2−4ac2a
where a=1,b=−50,c=1800:
u2=50±√(−50)2−4⋅1⋅18002⋅1
Calculating the discriminant:
u2=50±√2500−72002
This gives:
u2=50±√25002=50±302
The two solutions are:
u2=802=40andu2=202=10
However, since we are looking for the second position where the object distance is 30 cm, we find:
u2=30 cm
Both statements in the options are correct:
- The distance of the object from the convex lens in the other position is 30 cm.
- The distance between the object and the screen is 90 cm.
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:B. More than one option is correct
Explore 20 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:C. comprehension type question
Explore 14 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Integer type q.
Explore 14 Videos
- PROPERTIES OF MATTERBook:DC PANDEY ENGLISHChapter:PROPERTIES OF MATTERExercise:Integer
Explore 8 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
Similar Questions
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionA point object O is placed at a distance of 20cm from a convex lens of focal length 10cm as shown in the figure. At what distance x from the lens should a convex mirror of focal length 60cm, be placed so that final image coincide with the object?

View SolutionA point object is placed at a distance of 12cm from a convex lens of focal length 10cm. On the other side of the lens, a convex mirror is placed at a distance of 10cm from the lens such that the image formed by the combination coincides with the object itself. The focal length of the convex mirror is
View SolutionAn object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
nature of the image
View SolutionA luminous object is placed at a distance of 30 cm. from the convex lens of focal length 20 cm. On the other side of the lens, at what distance from the lens, a convex mirror of radius of curvature 10 cm. be placed in order to have an upright image of the object coincident with it ?
View SolutionAn object is placed at a distance of 40 cm from a convex lens of focal length 20cm. On the far side of the lens, a concave mirror of focal length 10cm is placed such that the distance of the object from the concave mirror is 100 cm. Then the final image which is formed after refraction from the lens, reflection from the mirror and again refraction from the lens, will be
View SolutionA point object O is placed at a distance of 20 cm from a convex lens of focal length 10 cm as shown in figure. At what distance x from the lens should a concave mirror of focal length 60 cm, placed so that final image coincides with the object ?

View SolutionAn object is placed at a distance of 20cm from a equi-concave lens of focal length 30cm, whose one surface is silvered. If the radius of curvature of the silvered surface is 60cm, find the position and nature of the image.
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View SolutionA plano-convex glass lens (μg=3/2) of radius of curvatureR=10cm is placed at a distance of b from a concave lens of focal length 20cm. What should be the distance a of point object O from the plano-convex lens so that position of final image is independent of b?
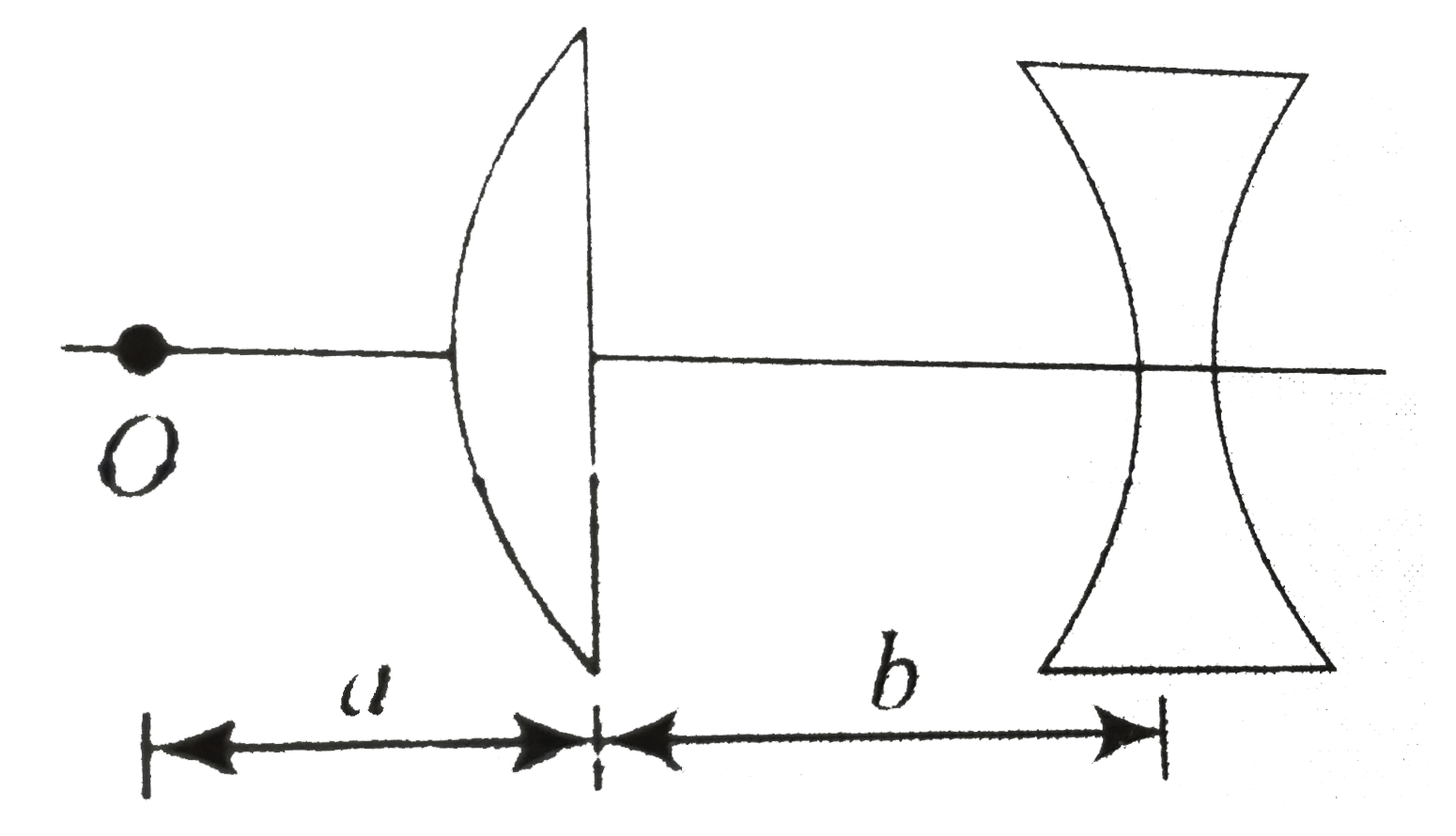
View Solution