Capacity of a spherical capacitor is C1 when inner sphere is charged and outer sphere is earthed and C2 when inner sphere is earthed and outer sphere charged. Then C1C2 is (a = radius of inner sphere b = radius of outer sphere)
1
ab
ba
a+ba−b
The correct Answer is:B
To find the ratio of the capacitances C1 and C2 of a spherical capacitor, we will follow these steps:
Step 1: Understand the Configuration
- For C1: The inner sphere (radius a) is charged with a charge Q, and the outer sphere (radius b) is earthed (grounded). This means the potential of the outer sphere is zero.
- For C2: The inner sphere is earthed, and the outer sphere is charged with a charge Q.
Step 2: Calculate C1
The capacitance C1 of the spherical capacitor when the inner sphere is charged and the outer sphere is earthed can be calculated using the formula:
C1=QV
where V is the potential difference between the inner and outer spheres.
The potential V at the surface of the inner sphere (radius a) is given by:
V=14πϵ0⋅Qa
Since the outer sphere is earthed (potential = 0), the potential difference V is simply:
V=Q4πϵ0a
Thus, the capacitance C1 becomes:
C1=QQ4πϵ0a=4πϵ0a
Step 3: Calculate C2
For C2, where the inner sphere is earthed and the outer sphere is charged, the capacitance can similarly be calculated:
C2=QV′
where V′ is the potential of the outer sphere when charged.
The potential V′ at the surface of the outer sphere (radius b) is given by:
V′=14πϵ0⋅Qb
Since the inner sphere is earthed (potential = 0), the potential difference V′ is:
V′=Q4πϵ0b
Thus, the capacitance C2 becomes:
C2=QQ4πϵ0b=4πϵ0b
Step 4: Find the Ratio C1C2
Now, we can find the ratio of the two capacitances:
C1C2=4πϵ0a4πϵ0b=ab
Final Answer
Thus, the ratio of the capacitances C1C2 is:
C1C2=ab
- For C1: The inner sphere (radius a) is charged with a charge Q, and the outer sphere (radius b) is earthed (grounded). This means the potential of the outer sphere is zero.
- For C2: The inner sphere is earthed, and the outer sphere is charged with a charge Q.
The capacitance C1 of the spherical capacitor when the inner sphere is charged and the outer sphere is earthed can be calculated using the formula:
C1=QV
where V is the potential difference between the inner and outer spheres.
V=14πϵ0⋅Qa
Since the outer sphere is earthed (potential = 0), the potential difference V is simply:
V=Q4πϵ0a
Thus, the capacitance C1 becomes:
C1=QQ4πϵ0a=4πϵ0a
For C2, where the inner sphere is earthed and the outer sphere is charged, the capacitance can similarly be calculated:
C2=QV′
where V′ is the potential of the outer sphere when charged.
V′=14πϵ0⋅Qb
Since the inner sphere is earthed (potential = 0), the potential difference V′ is:
V′=Q4πϵ0b
Thus, the capacitance C2 becomes:
C2=QQ4πϵ0b=4πϵ0b
Now, we can find the ratio of the two capacitances:
C1C2=4πϵ0a4πϵ0b=ab
Thus, the ratio of the capacitances C1C2 is:
C1C2=ab
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.
View SolutionCharge on the outer sphere is q, and the inner sphere is grounded. Then the charge q' on the inner sphere is q', for
(r2>r1)

View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionA sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
View SolutionThe capacity of an isolated sphere is increased n times when it is enclosed by an earthed concentric sphere. The ratio of their radii is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionConsider two concentric metal spheres. The outer sphere is given a charge Q>0, then
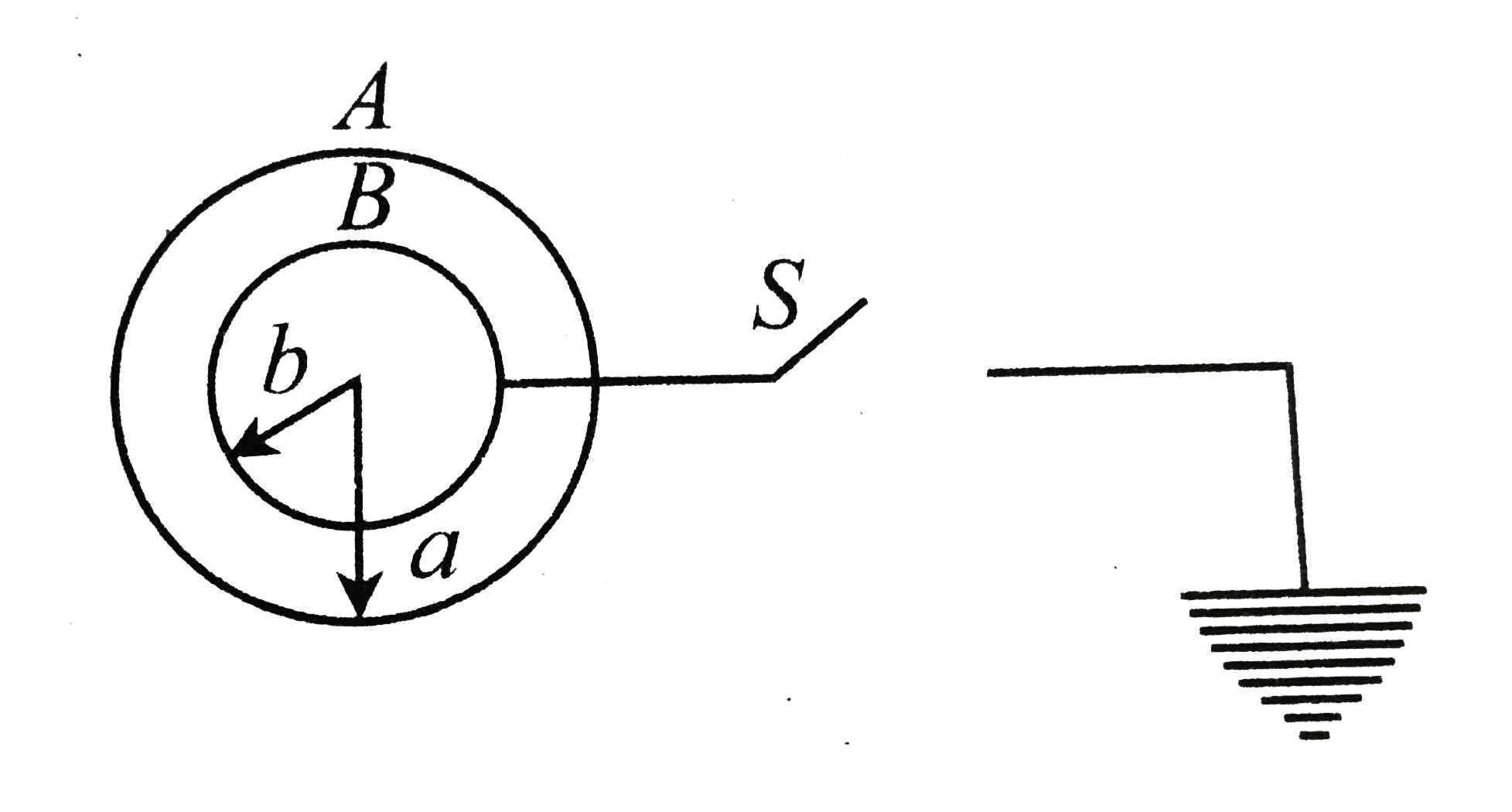 ,
,
View SolutionA sphere of radius 0.03m is suspended within a hollow sphere of radius 0.05m. If the inner sphere is charged to a potential of 1500 volt and outer sphere is earthed. Find the capacitance and the charge of the inner sphere.
View SolutionConsider two concentric conducting spheres. The outer sphere is hollow and initially has a charge −7Q on it. The inner sphere is solid and has a charge +2Q on it.
a. How much charge is on the outer surface and inner surface of the outer sphere.
b. If a wire is connected between the inner and outer sphere, after electrostatic equilibrium is established how much total charge is on the outer sphere? How much charge is on the outer surface and inner surface of the outer sphere? Does the electric field at the surface of the inside sphere change when the wire is connected?
c. We return to original condition in (a). We now connect the outer sphere to ground with a wire and then disconnect it. How much total charge will be on the outer sphere? How much charge will be on the inner surface and outer surface of the outer sphere?
View Solution
