A sphere of radius 0.03m is suspended within a hollow sphere of radius 0.05m. If the inner sphere is charged to a potential of 1500 volt and outer sphere is earthed. Find the capacitance and the charge of the inner sphere.
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- Radius of the inner sphere (A) = 0.03 m
- Radius of the outer sphere (B) = 0.05 m
- Potential of the inner sphere (V) = 1500 V
- The outer sphere is earthed, so its potential is 0 V.
Step 2: Write the formula for the capacitance of a spherical capacitor
The formula for the capacitance C of a spherical capacitor is given by:
C=4πϵ0ABB−A
where:
- ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Step 3: Substitute the values into the capacitance formula
Substituting the values of A and B:
C=4π(8.85×10−12)(0.03)(0.05)0.05−0.03
Step 4: Calculate the denominator
Calculating B−A:
B−A=0.05−0.03=0.02m
Step 5: Calculate the capacitance
Now substituting back into the capacitance formula:
C=4π(8.85×10−12)(0.03)(0.05)0.02
Calculating the numerator:
4π(8.85×10−12)(0.03)(0.05)≈5.27×10−13F
Now dividing by the denominator:
C=5.27×10−130.02≈2.635×10−11F=26.35pF
Step 6: Calculate the charge on the inner sphere
Using the relationship between charge Q, capacitance C, and voltage V:
Q=C⋅V
Substituting the values:
Q=(2.635×10−11F)⋅(1500V)
Step 7: Perform the multiplication
Calculating Q:
Q=3.9525×10−8C≈3.95×10−8C
Final Results
- Capacitance C≈26.35pF
- Charge Q≈3.95×10−8C
---
- Radius of the inner sphere (A) = 0.03 m
- Radius of the outer sphere (B) = 0.05 m
- Potential of the inner sphere (V) = 1500 V
- The outer sphere is earthed, so its potential is 0 V.
The formula for the capacitance C of a spherical capacitor is given by:
C=4πϵ0ABB−A
where:
- ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m.
Substituting the values of A and B:
C=4π(8.85×10−12)(0.03)(0.05)0.05−0.03
Calculating B−A:
B−A=0.05−0.03=0.02m
Now substituting back into the capacitance formula:
C=4π(8.85×10−12)(0.03)(0.05)0.02
Calculating the numerator:
4π(8.85×10−12)(0.03)(0.05)≈5.27×10−13F
Now dividing by the denominator:
C=5.27×10−130.02≈2.635×10−11F=26.35pF
Using the relationship between charge Q, capacitance C, and voltage V:
Q=C⋅V
Substituting the values:
Q=(2.635×10−11F)⋅(1500V)
Calculating Q:
Q=3.9525×10−8C≈3.95×10−8C
- Capacitance C≈26.35pF
- Charge Q≈3.95×10−8C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:Check point 2.1
Explore 15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:Check point 2.2
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Medical entrances gallery
Explore 37 Videos
Similar Questions
A sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA hollow metallic sphere of radius 0.1 m is charged to a potential of 5 V. The potential at its centre is
View SolutionFigure shows a solid conducting sphere of radius 1 m. enclosed by a metallic shell of radius 3 m such that their centress coincide. If outer shell is given a charge of 6 μC and inner sphere is earthed, find megnitude charge on the surface of inner shell

View SolutionA conducting sphere of radius R is charged to a potential of V volts. Then the electric field at a distance r(>R) from the centre of the sphere would be
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View SolutionA solid sphere of radius R has a charge +2Q. A hollow spherical concentric with the first sphere that has net charge -Q.
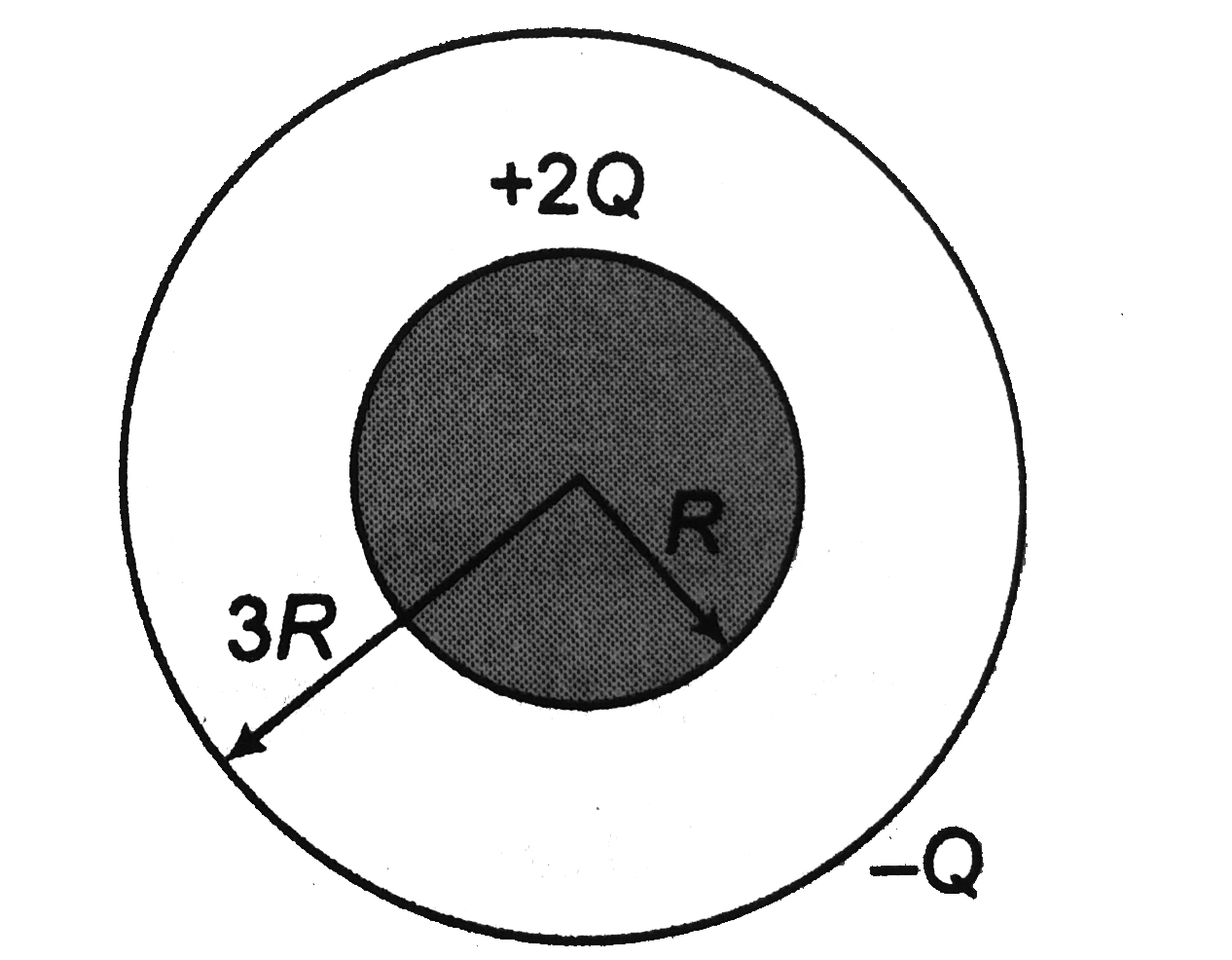
(a) Find the electric field between the spheres at a distance r from the centre of the inner sphere. [R<r<3R]
(b) Calculate the potential difference between the spheres.
(c) What would be the final distribution of charges, if a conducting wire joins the spheres?
(d) Instead of (c), if the inner sphere is earthed, what is the charge on it?
View SolutionA hollow metal sphere of radius 6 cm is charged such that the potential on its surface is 12 V.What is the potential at the centre of the sphere?
View SolutionA hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
View Solution