The capacitance of a capacitor becomes4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric constant of the slab?
2
4
6
8
The correct Answer is:A
To solve the problem, we need to determine the dielectric constant k of a dielectric slab that is inserted between the plates of a capacitor, which increases the capacitance to 43 times its original value. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Original Capacitance
The original capacitance C0 of a capacitor with a separation d between its plates and with vacuum (or air) as the dielectric is given by:
C0=ε0Ad
where A is the area of the plates and ε0 is the permittivity of free space.
Step 2: Insert the Dielectric Slab
When a dielectric slab of thickness t=d2 is inserted, the remaining space between the plates is filled with air. Thus, the capacitor can be viewed as two capacitors in series:
1. The first capacitor (with the dielectric slab) has a capacitance C1.
2. The second capacitor (with air) has a capacitance C2.
Step 3: Calculate the Capacitance with Dielectric
The capacitance C1 of the portion with the dielectric slab is given by:
C1=kε0Ad2=2kε0Ad
where k is the dielectric constant of the slab.
Step 4: Calculate the Capacitance with Air
The capacitance C2 of the portion with air is:
C2=ε0Ad2=2ε0Ad
Step 5: Find the Equivalent Capacitance
The total capacitance C of two capacitors in series is given by:
1C=1C1+1C2
Substituting the expressions for C1 and C2:
1C=d2kε0A+d2ε0A
Combining the fractions:
1C=d(1+k)2kε0A
Thus, the equivalent capacitance C becomes:
C=2kε0Ad(1+k)
Step 6: Set Up the Equation
According to the problem, the new capacitance C is 43C0:
2kε0Ad(1+k)=43⋅ε0Ad
Step 7: Simplify the Equation
Canceling ε0A/d from both sides gives:
2k=43(1+k)
Step 8: Solve for k
Multiplying through by 3 to eliminate the fraction:
6k=4(1+k)
Expanding the right side:
6k=4+4k
Rearranging gives:
6k−4k=4
2k=4⇒k=2
Final Answer
The dielectric constant k of the slab is:
2
The original capacitance C0 of a capacitor with a separation d between its plates and with vacuum (or air) as the dielectric is given by:
C0=ε0Ad
where A is the area of the plates and ε0 is the permittivity of free space.
When a dielectric slab of thickness t=d2 is inserted, the remaining space between the plates is filled with air. Thus, the capacitor can be viewed as two capacitors in series:
1. The first capacitor (with the dielectric slab) has a capacitance C1.
2. The second capacitor (with air) has a capacitance C2.
The capacitance C1 of the portion with the dielectric slab is given by:
C1=kε0Ad2=2kε0Ad
where k is the dielectric constant of the slab.
The capacitance C2 of the portion with air is:
C2=ε0Ad2=2ε0Ad
The total capacitance C of two capacitors in series is given by:
1C=1C1+1C2
Substituting the expressions for C1 and C2:
1C=d2kε0A+d2ε0A
Combining the fractions:
1C=d(1+k)2kε0A
Thus, the equivalent capacitance C becomes:
C=2kε0Ad(1+k)
According to the problem, the new capacitance C is 43C0:
2kε0Ad(1+k)=43⋅ε0Ad
Canceling ε0A/d from both sides gives:
2k=43(1+k)
Multiplying through by 3 to eliminate the fraction:
6k=4(1+k)
Expanding the right side:
6k=4+4k
Rearranging gives:
6k−4k=4
2k=4⇒k=2
The dielectric constant k of the slab is:
2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
The capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionThe capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionWhen a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionA capacitor and a bulb are connected in series with a source of alternating emf. If a dielectric slab is inserted between the plates of the capacitor, then
View SolutionThe plates of a parallel plate capacitor are charged up to 200 V. A dielectric slab of thickness 4 mm is inserted between its plates. Then, to maintain the same potential difference between the plates of the capacitor, the distance between the plates increased by 3.2 mm. The dielectric constant of the dielectric slab is
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
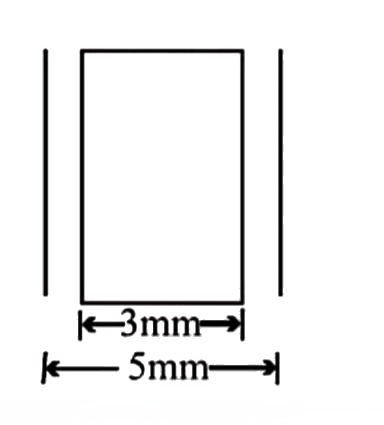
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
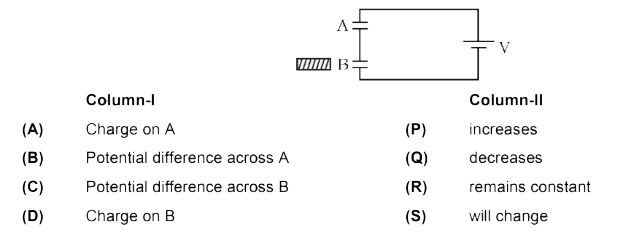
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View Solution
