The capacitance of a capacitor between4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric consant of the slab?
To solve the problem, we need to find the dielectric constant K of a dielectric slab that is inserted between the plates of a capacitor. The capacitance of the capacitor increases to 43 times its original value when the slab is inserted.
1. Identify the Original Capacitance:
The original capacitance C of the capacitor is given by the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
2. Insert the Dielectric Slab:
When a dielectric slab of thickness t=d2 is inserted, the remaining air gap between the plates is also d2. The new capacitance C′ can be calculated using the formula for capacitors in series:
C′=ε0Ad−t+tK
Here, K is the dielectric constant of the slab.
3. Substituting Values:
Substitute t=d2 into the equation:
C′=ε0Ad−d2+d2K
This simplifies to:
C′=ε0Ad2+d2K
C′=2ε0Ad+d2K
4. Equating New Capacitance to Increased Value:
We know that C′=43C:
2ε0Ad+d2K=43(ε0Ad)
5. Simplifying the Equation:
Substitute C into the equation:
2ε0Ad+d2K=4ε0A3d
Rearranging gives:
2ε0Ad−4ε0A3d+d2K=0
To combine the terms, find a common denominator:
6ε0A3d−4ε0A3d+d2K=0
This simplifies to:
2ε0A3d+d2K=0
6. Solving for K:
Multiply through by 3dK to eliminate the denominators:
2ε0AK+3d22=0
Rearranging gives:
2ε0AK=3d22
Thus,
K=3d24ε0A
7. Final Calculation:
Since we need to find K in terms of the original capacitance:
From the earlier steps, we can simplify to find:
4K+4=6K⟹2K=4⟹K=2
Conclusion:
The dielectric constant K of the slab is 2.
The original capacitance C of the capacitor is given by the formula:
C=ε0Ad
where ε0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
When a dielectric slab of thickness t=d2 is inserted, the remaining air gap between the plates is also d2. The new capacitance C′ can be calculated using the formula for capacitors in series:
C′=ε0Ad−t+tK
Here, K is the dielectric constant of the slab.
Substitute t=d2 into the equation:
C′=ε0Ad−d2+d2K
This simplifies to:
C′=ε0Ad2+d2K
C′=2ε0Ad+d2K
We know that C′=43C:
2ε0Ad+d2K=43(ε0Ad)
Substitute C into the equation:
2ε0Ad+d2K=4ε0A3d
Rearranging gives:
2ε0Ad−4ε0A3d+d2K=0
To combine the terms, find a common denominator:
6ε0A3d−4ε0A3d+d2K=0
This simplifies to:
2ε0A3d+d2K=0
Multiply through by 3dK to eliminate the denominators:
2ε0AK+3d22=0
Rearranging gives:
2ε0AK=3d22
Thus,
K=3d24ε0A
Since we need to find K in terms of the original capacitance:
From the earlier steps, we can simplify to find:
4K+4=6K⟹2K=4⟹K=2
The dielectric constant K of the slab is 2.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Fill in the blanks
Explore 10 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:True and False Type
Explore 5 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 3Exercise:Comprehension Type
Explore 94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBook:CENGAGE PHYSICS ENGLISHChapter:MAGNETIC FIELD AND MAGNETIC FORCESExercise:Multiple Correct Answer type
Explore 2 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICS ENGLISHChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
Similar Questions
The capacitance of a capacitor becomes4/3 times its original value if a dielectric slab of thickness t=d/2 is inserted between the plates (d is the separation between the plates). What is the dielectric constant of the slab?
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionWhen a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionThe plates of a parallel plate capacitor are charged up to 200 V. A dielectric slab of thickness 4 mm is inserted between its plates. Then, to maintain the same potential difference between the plates of the capacitor, the distance between the plates increased by 3.2 mm. The dielectric constant of the dielectric slab is
View SolutionA capacitor and a bulb are connected in series with a source of alternating emf. If a dielectric slab is inserted between the plates of the capacitor, then
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=d2 but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
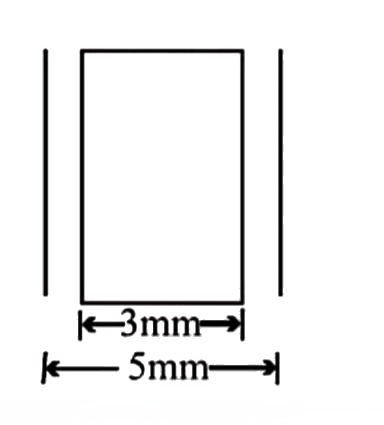
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
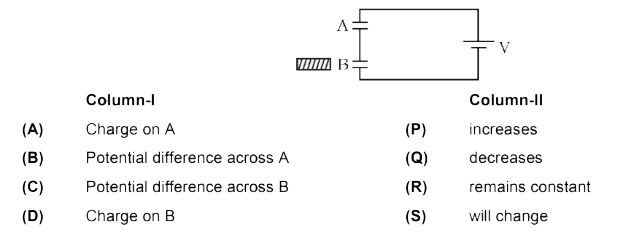
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionA parallel plate capacitor is charged by a battery. After some time the battery is disconnected and a dielectric slab of dielectric constant K is inserted between the plates. How would (i) the capacitance, (ii) the electric field between the plates and (iii) the energy stored in the capacitor, be affected ? Justify your answer.
View Solution