Time constant of a C-R circuit is 2ln(2) second. Capacitor is discharged at time t=0. The ratio of charge on the capacitor at time t=2s and t=6s is
3:1
8:1
4:1
2:1
The correct Answer is:C
To find the ratio of charge on the capacitor at time t=2s and t=6s in a C-R circuit, we can use the formula for the charge Q(t) on a discharging capacitor, which is given by:
Q(t)=Q0e−t/τ
where:
- Q0 is the initial charge on the capacitor,
- τ is the time constant of the circuit,
- t is the time in seconds.
Given that the time constant τ=2ln(2) seconds, we can calculate the charges at t=2s and t=6s.
Step 1: Calculate the charge at t=2s
Using the formula:
Q(2)=Q0e−2/τ
Substituting τ=2ln(2):
Q(2)=Q0e−2/(2ln(2))=Q0e−ln(2)=Q0⋅12=Q02
Step 2: Calculate the charge at t=6s
Using the same formula:
Q(6)=Q0e−6/τ
Substituting τ=2ln(2):
Q(6)=Q0e−6/(2ln(2))=Q0e−3ln(2)=Q0⋅(eln(2))−3=Q0⋅(12)3=Q0⋅18=Q08
Step 3: Calculate the ratio of charges
Now we can find the ratio of the charges at t=2s and t=6s:
Ratio=Q(2)Q(6)=Q02Q08=Q02⋅8Q0=82=4
Thus, the ratio of charge on the capacitor at t=2s and t=6s is 4:1.
Final Answer:
The ratio of charge on the capacitor at t=2s and t=6s is 4:1.
---
- Q0 is the initial charge on the capacitor,
- τ is the time constant of the circuit,
- t is the time in seconds.
The ratio of charge on the capacitor at t=2s and t=6s is 4:1.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
The switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
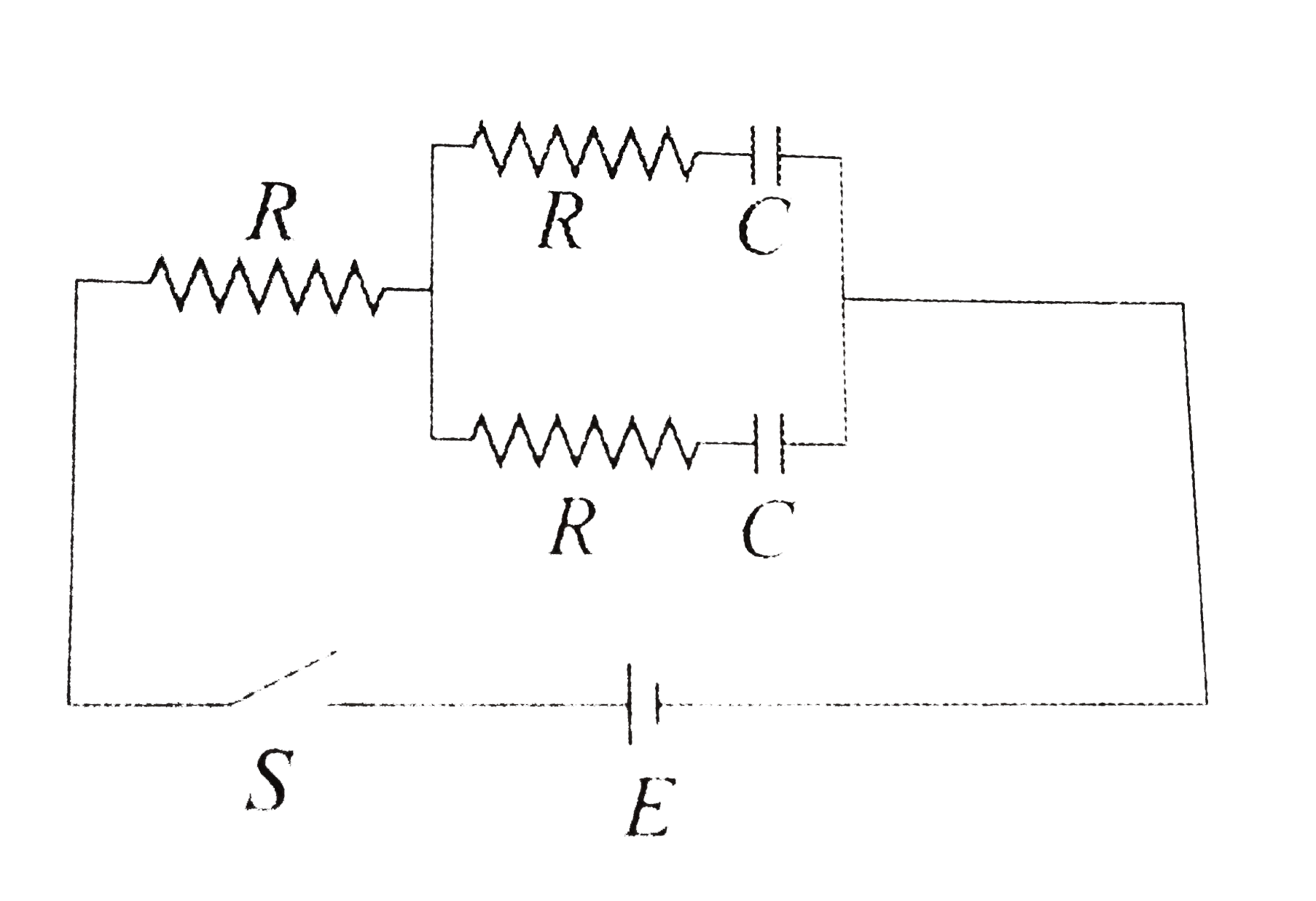
View SolutionThere is no resistance in the capacitive circuit shown. Then charge on the capacitor at an time t

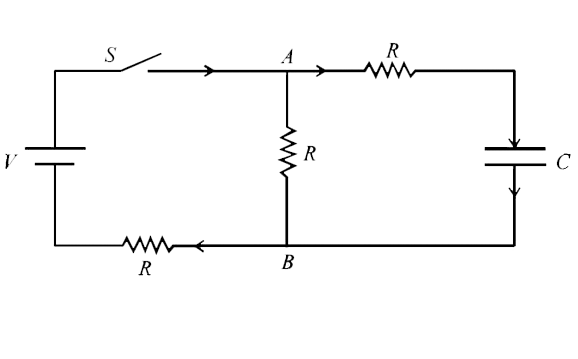
View SolutionIn the circuit shown in Figure, the battery is an ideal one, with emf V. The capacitor is initially uncharged. The switch S is closed at time t = 0 .
(a) Find the charge Q on the capacitor at time t.
(b) Find the current in AB at time t. What is its liniting value as t→∞:
 .
.
View SolutionThe time constant T for the shown circuit containing resistance and capacitor, is
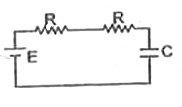
View SolutionInitially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionA capacitor is charged to a certain potential and then allowed to discharge through a resistance R. The ratio of charge on the capacitor to current in the circuit
View SolutionIn the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is

View SolutionA capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)
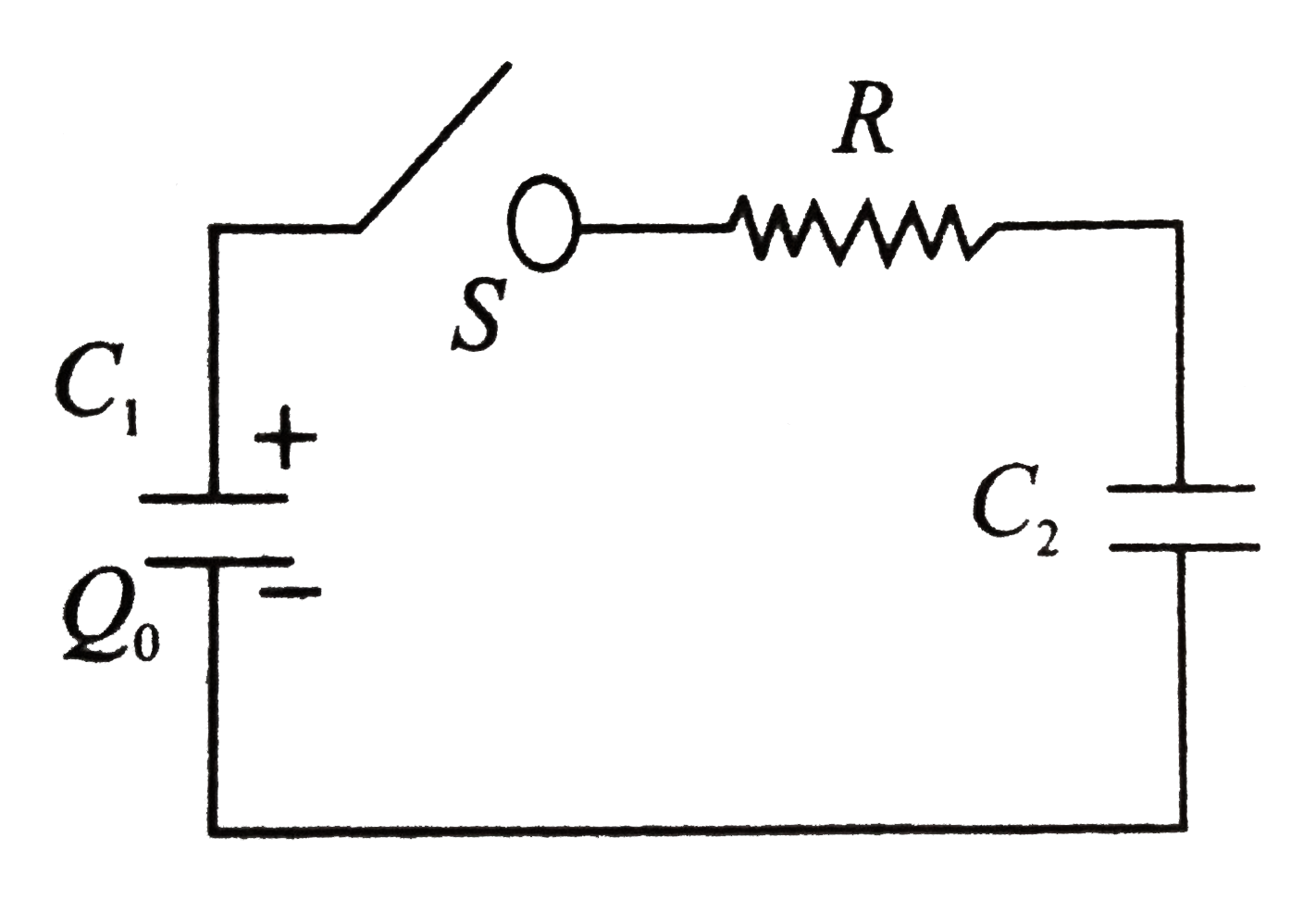
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
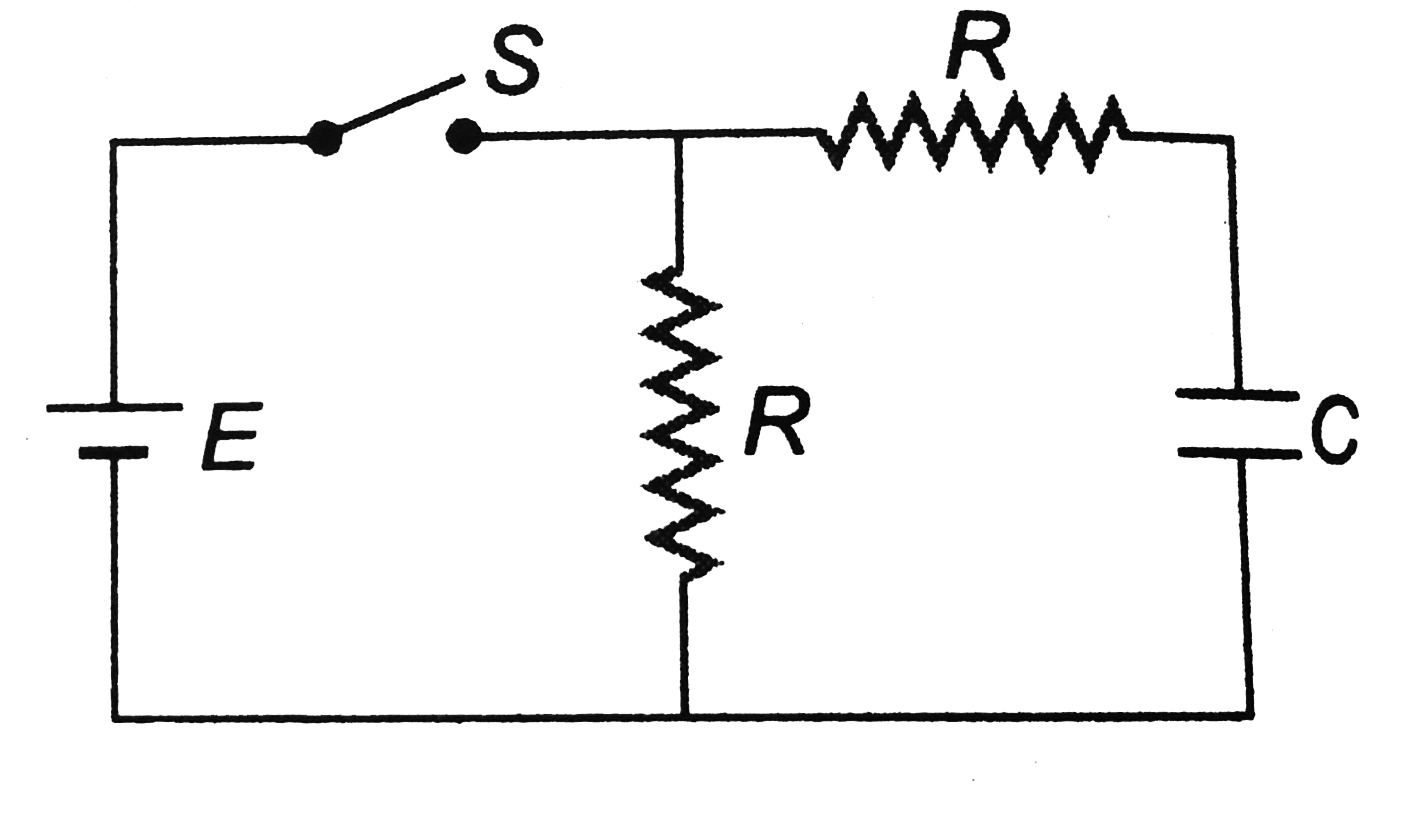
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View Solution
