Two thin long parallel wires seperated by a distance 'b' are carrying a current ' I' amp each . The magnitude of the force3 per unit length exerted by one wire on the other is
μ0i2b2
μ0i22πb2
μ0i22πb
μ0i2πb2
The correct Answer is:C
To solve the problem of finding the magnitude of the force per unit length exerted by one long parallel wire on another, we can follow these steps:
1. Understanding the Setup:
- We have two long parallel wires, separated by a distance b.
- Both wires carry the same current I in the same direction.
2. Magnetic Field Due to One Wire:
- The magnetic field B created by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
- In our case, the distance r is equal to b (the distance between the two wires). Therefore, the magnetic field B at the location of the second wire (due to the first wire) is:
B=μ0I2πb
3. Force on the Second Wire:
- The force F experienced by a segment of wire carrying current I in a magnetic field B is given by:
F=I⋅L⋅B
- Here, L is the length of the wire segment we are considering. For per unit length, we can set L=1 meter, so:
F=I⋅B
4. Substituting the Magnetic Field:
- Now, substituting the expression for B into the force equation, we get:
F=I⋅(μ0I2πb)
- Simplifying this gives:
F=μ0I22πb
5. Force per Unit Length:
- Since we are looking for the force per unit length, we can express it as:
Force per unit length=FL=μ0I22πb
Final Answer:
The magnitude of the force per unit length exerted by one wire on the other is:
μ0I22πb
- We have two long parallel wires, separated by a distance b.
- Both wires carry the same current I in the same direction.
- The magnetic field B created by a long straight wire carrying current I at a distance r from the wire is given by the formula:
B=μ0I2πr
- In our case, the distance r is equal to b (the distance between the two wires). Therefore, the magnetic field B at the location of the second wire (due to the first wire) is:
B=μ0I2πb
- The force F experienced by a segment of wire carrying current I in a magnetic field B is given by:
F=I⋅L⋅B
- Here, L is the length of the wire segment we are considering. For per unit length, we can set L=1 meter, so:
F=I⋅B
- Now, substituting the expression for B into the force equation, we get:
F=I⋅(μ0I2πb)
- Simplifying this gives:
F=μ0I22πb
- Since we are looking for the force per unit length, we can express it as:
Force per unit length=FL=μ0I22πb
The magnitude of the force per unit length exerted by one wire on the other is:
μ0I22πb
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
Two thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionTwo long straight parallel conductors separated by a distance of 0.5m carry currents of 5A and 8A in the same direction. The force per unit length experienced by each other is
View Solution
Knowledge Check
Two parallel wires 2 m apart carry currents of 2 A and 5 A respectively in same direction, the force per unit length acting between these two wires is
A2×10−6Nm−1B3×10−6Nm−1C1×10−6Nm−1D4×10−6Nm−1
Two infinite, parallel wires are a distance 10 cm apart and carry equal current 20 A in the same direction. The magnetic force on a 1 cm long segment of one wire due to the other wire is ___________ ×10−6N. (Permeabilityi of vacuum μ0=4π×10−7N/A2)
View SolutionTwo long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionIn Fig. two long parallel wires (seen end-on) that are a distance R apart carry equal currents i in the same sense. Find the magnitude of the magnetic field at point P , which lies quidistant from the two wires at an angle θ from the plane of the wires.

View SolutionAn arrangment of three parallel staright wires placed perpendcular to plane of paper carrying same current I along the same direction is shown in figure. Magnitude of force per unit length on the middle wire 'B' is given by
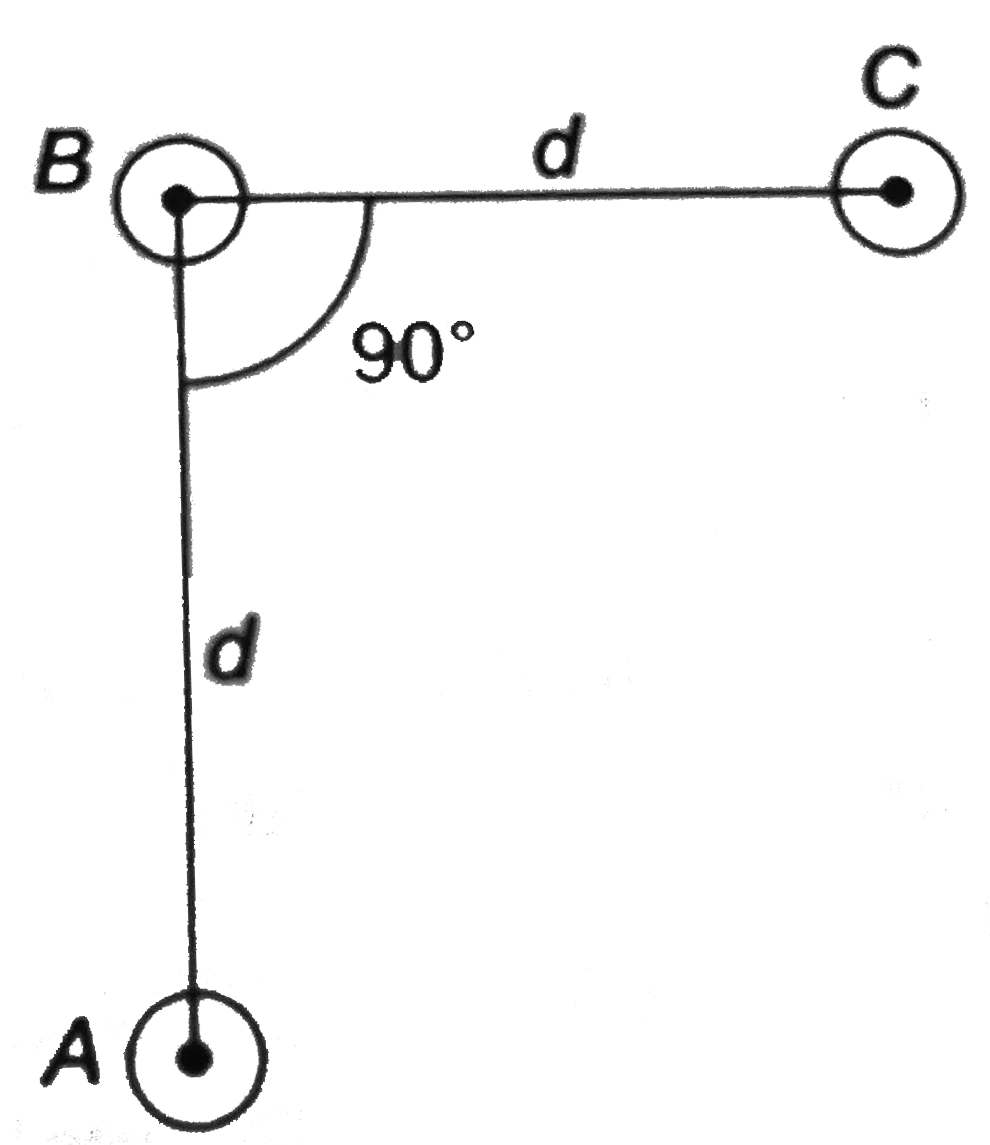
View SolutionTwo long parallel wires are 30 cm apart carrying currents 10 A and 15 A respectively in the same direction. The force acting over a length of 5 m of the wires is
View SolutionTwo long parallel wires are separated by a distance of 2.50cm. The force per unit length that each wire exerts on the other is 4.00×10−5Nm, and the wires repel each other. The current in one wire is 0.600A.
a. What is the current in the second wire ?
b. Are the two currents in the same direction or in opposite direction?
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View Solution
