A charge particle having charge q expericenec a F1q=(−ˆj+ˆk)N in a magnetic field B when is has velocity v1=(1.0)ˆims. The force becomes F=q(ˆi−ˆk) when the velocity is charged to v2=1.0ˆjms magnetic induction vector at that point is
(ˆi+ˆj+ˆk)T
(ˆi−ˆj−ˆk)T
(−ˆi−ˆj+ˆk)T
(ˆi+ˆj−ˆk)T
The correct Answer is:A
Step by step video & image solution for A charge particle having charge q expericenec a F_(1)q=(-hatj+hatk)N in a magnetic field B when is has velocity v_(1)=(1.0)hati(m)/(s). The force becomes F=q(hati-hatk) when the velocity is charged to v_2 = 1.0hatj(m)/(s) magnetic induction vector at that point is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Comprehension type Questions
16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
A charged particle has acceleration →a=2ˆi+xˆj in a magnetic field →B=−3ˆi+2ˆj−4ˆk.Find the value of x.
View SolutionA positive charge particle having change q and mass m has velocity →v=v(ˆi+ˆk√2) in the magnetic field B at the origin . Its speed as the function of y is :
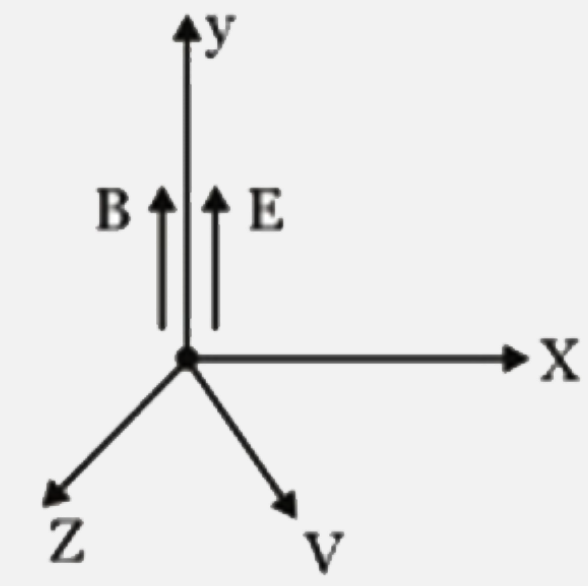
View SolutionA charge q is moving with a velocity v1=1ˆi m/s at a point in a magentic field and experiences a force F=q[−ˆj+1ˆk] N. If the charge is moving with a voloctiy v2=ˆj m/s at the same point then it experiences a force F2=q(1ˆi−1ˆk) N. The magnetic induction B at that point is
View SolutionThe velocity of a particle is v=6ˆi+2ˆj−2ˆk The component of the velocity parallel to vector a=ˆi+ˆj+ˆk in vector from is
View SolutionA particle of spectfic charge α enters a uniform magnetic field B=−B0ˆk with velocity V=v0ˆi from the origin Find the time dependence of velocity and position of the particle
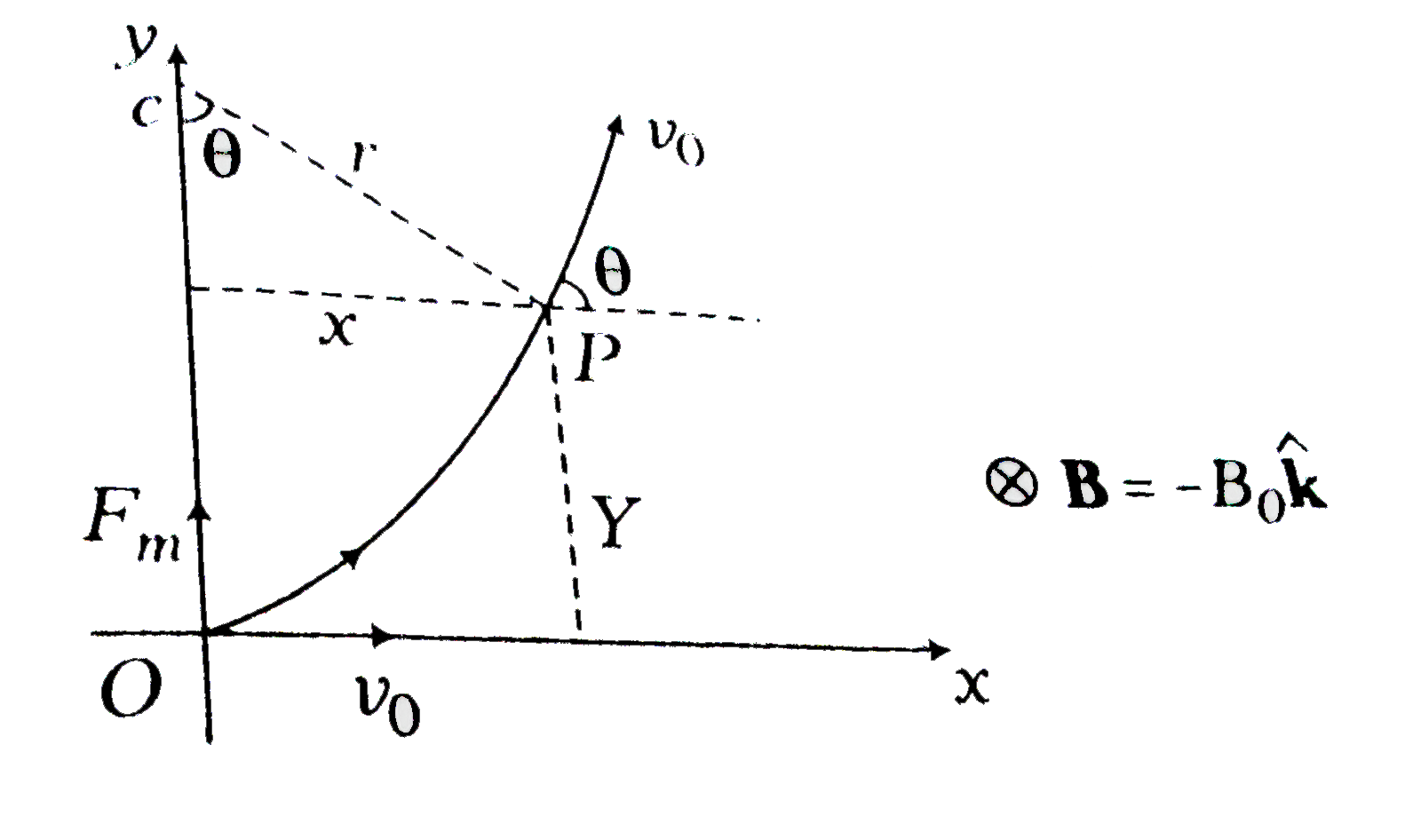
View SolutionA charge q enters into a magnetic field (B) perpendicularly with velocity V. The time rate of work done by the magnetic force on the charge is
View SolutionA charged particle of unit mass and unit charge moves with velocity →v=(8ˆi+6ˆj)ms−1 in magnetic field of →B=2ˆkT. Choose the correct alternative (s).
View SolutionA charged particle of unit mass and unit charge moves with velocity →v=(8ˆi+6ˆj)ms−1 in magnetic field of →B=2ˆkT. Choose the correct alternative (s).
View SolutionA force →F=(2ˆi+ˆj+ˆk)N is acting on a particle moving with constant velocity →v=(ˆi+2ˆj+ˆk)m/s. Power delivered by force is
View SolutionA particle having charge q moves with a velocity v through a region in which both an electric field →E and a magnetic field B are present. The force on the particle is
View Solution
