An α is moving along a circle of radius R with a constant angular velocity ω. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by the α-particle. If the minimum time interval between two successive time at which A records zero magnetic field is t, the angular speed ω, in terms of t, is
2πt
2π3t
π3t
π2t
The correct Answer is:b
To solve the problem, we need to analyze the motion of the alpha particle and how it affects the magnetic field at point A.
1. Understanding the Setup:
- An alpha particle is moving in a circular path of radius R with a constant angular velocity ω.
- Point A is located at a distance 2R from the center of the circle.
2. Magnetic Field Calculation:
- The magnetic field B at point A due to a current element dl of the moving charge can be calculated using the Biot-Savart law:
B=μ04π∫Idl×rr3
- Here, r is the position vector from the current element to point A.
3. Condition for Zero Magnetic Field:
- The magnetic field at point A will be zero when the angle θ between the velocity vector v of the alpha particle and the position vector r from the alpha particle to point A is either 0∘ (parallel) or 180∘ (antiparallel).
- As the alpha particle moves in a circle, it will create a zero magnetic field at point A at specific positions.
4. Finding the Angles:
- The distance from the center to point A is 2R, and the radius of the circular path of the alpha particle is R.
- Using the cosine rule, when the angle θ is 60∘, the cosine of the angle between the position vector and the velocity vector is:
cosθ=R2R=12
- This indicates that the angle θ is 60∘.
5. Time Interval Calculation:
- The alpha particle moves 120∘ (or 2π3 radians) between the two positions where the magnetic field at point A is zero.
- The angular displacement Δθ in terms of angular velocity ω and time t is given by:
Δθ=ω⋅t
- Since Δθ=2π3, we can write:
ω⋅t=2π3
6. Expressing Angular Velocity:
- Rearranging the equation gives us:
ω=2π3t
Final Answer:
Thus, the angular speed ω in terms of t is:
ω=2π3t
- An alpha particle is moving in a circular path of radius R with a constant angular velocity ω.
- Point A is located at a distance 2R from the center of the circle.
- The magnetic field B at point A due to a current element dl of the moving charge can be calculated using the Biot-Savart law:
B=μ04π∫Idl×rr3
- Here, r is the position vector from the current element to point A.
- The magnetic field at point A will be zero when the angle θ between the velocity vector v of the alpha particle and the position vector r from the alpha particle to point A is either 0∘ (parallel) or 180∘ (antiparallel).
- As the alpha particle moves in a circle, it will create a zero magnetic field at point A at specific positions.
- The distance from the center to point A is 2R, and the radius of the circular path of the alpha particle is R.
- Using the cosine rule, when the angle θ is 60∘, the cosine of the angle between the position vector and the velocity vector is:
cosθ=R2R=12
- This indicates that the angle θ is 60∘.
- The alpha particle moves 120∘ (or 2π3 radians) between the two positions where the magnetic field at point A is zero.
- The angular displacement Δθ in terms of angular velocity ω and time t is given by:
Δθ=ω⋅t
- Since Δθ=2π3, we can write:
ω⋅t=2π3
- Rearranging the equation gives us:
ω=2π3t
Thus, the angular speed ω in terms of t is:
ω=2π3t
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:More than One Option is Correct
Explore 25 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Comprehension type Questions
Explore 16 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEY ENGLISHChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Integer type Questions
Explore 10 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEY ENGLISHChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
Similar Questions
A particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
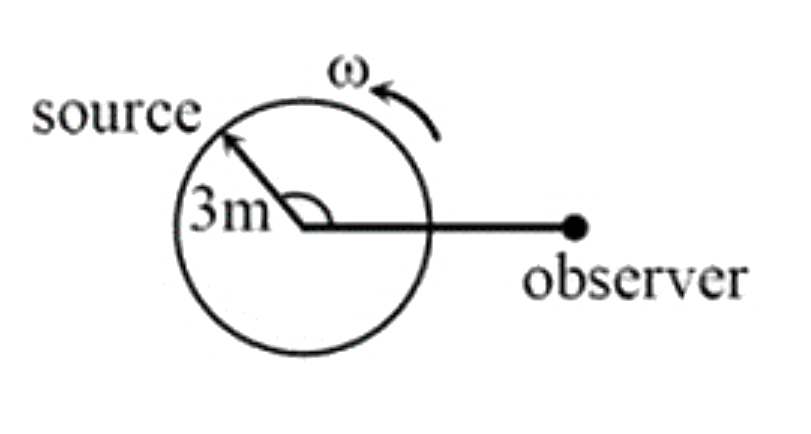
View SolutionA source is moving on a circle of radius 3m with constant angular velocity ω=5rads−1. If the observer is at a distnace 5 cm from the centre of the circle, the time interval between the maximum and minimum frequency recived by the observer is
View SolutionThe magnitude of displacement of a particle moving in a circle of radius a with constant angular speed ω varries with time t is
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View SolutionA point mass moves along a circle of radius R with a constant angular acceleration α. How much time is needed after motion begins for the radial acceleration of the point mass to be equal to its tangential acceleration ?
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View Solution