Velocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
y=bx3/2a+c
y=4√2b3(xa)3/2+c
y=4√2b3(xa)3/2−c
y=bx3/2a−c
The correct Answer is:A
To find the trajectory of the particle given its velocity as v=a^i+2bt2^j and that it starts from the point (0,c), we will follow these steps:
Step 1: Identify the components of velocity
The velocity vector can be broken down into its components:
- In the x-direction: vx=a
- In the y-direction: vy=2bt2
Step 2: Write the equations for displacement
Using the relationship between velocity and displacement, we can express the displacements in the x and y directions:
- For the x-direction:
dxdt=a⟹dx=adt
- For the y-direction:
dydt=2bt2⟹dy=2bt2dt
Step 3: Integrate to find the position functions
Now, we will integrate both equations to find the position as a function of time.
1. Integrate for x:
x=∫adt=at+Cx
Since the particle starts at x=0 when t=0:
0=a(0)+Cx⟹Cx=0⟹x=at
2. Integrate for y:
y=∫2bt2dt=2bt33+Cy
Since the particle starts at y=c when t=0:
c=2b(0)33+Cy⟹Cy=c⟹y=2bt33+c
Step 4: Eliminate time to find the trajectory
Now we have:
- x=at
- y=2bt33+c
From the first equation, we can express t in terms of x:
t=xa
Substituting this expression for t into the equation for y:
y=2b3(xa)3+c
y=2b3a3x3+c
Final Result
The trajectory of the particle is given by:
y=2b3a3x3+c
The velocity vector can be broken down into its components:
- In the x-direction: vx=a
- In the y-direction: vy=2bt2
Using the relationship between velocity and displacement, we can express the displacements in the x and y directions:
- For the x-direction:
dxdt=a⟹dx=adt
- For the y-direction:
dydt=2bt2⟹dy=2bt2dt
Now, we will integrate both equations to find the position as a function of time.
x=∫adt=at+Cx
Since the particle starts at x=0 when t=0:
0=a(0)+Cx⟹Cx=0⟹x=at
y=∫2bt2dt=2bt33+Cy
Since the particle starts at y=c when t=0:
c=2b(0)33+Cy⟹Cy=c⟹y=2bt33+c
Now we have:
- x=at
- y=2bt33+c
t=xa
y=2b3(xa)3+c
y=2b3a3x3+c
The trajectory of the particle is given by:
y=2b3a3x3+c
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionAcceleration of a particle at any time t is →a=(2tˆi+3t2ˆj)m/s2.If initially particle is at rest, find the velocity of the particle at time t=2s
View SolutionThe velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
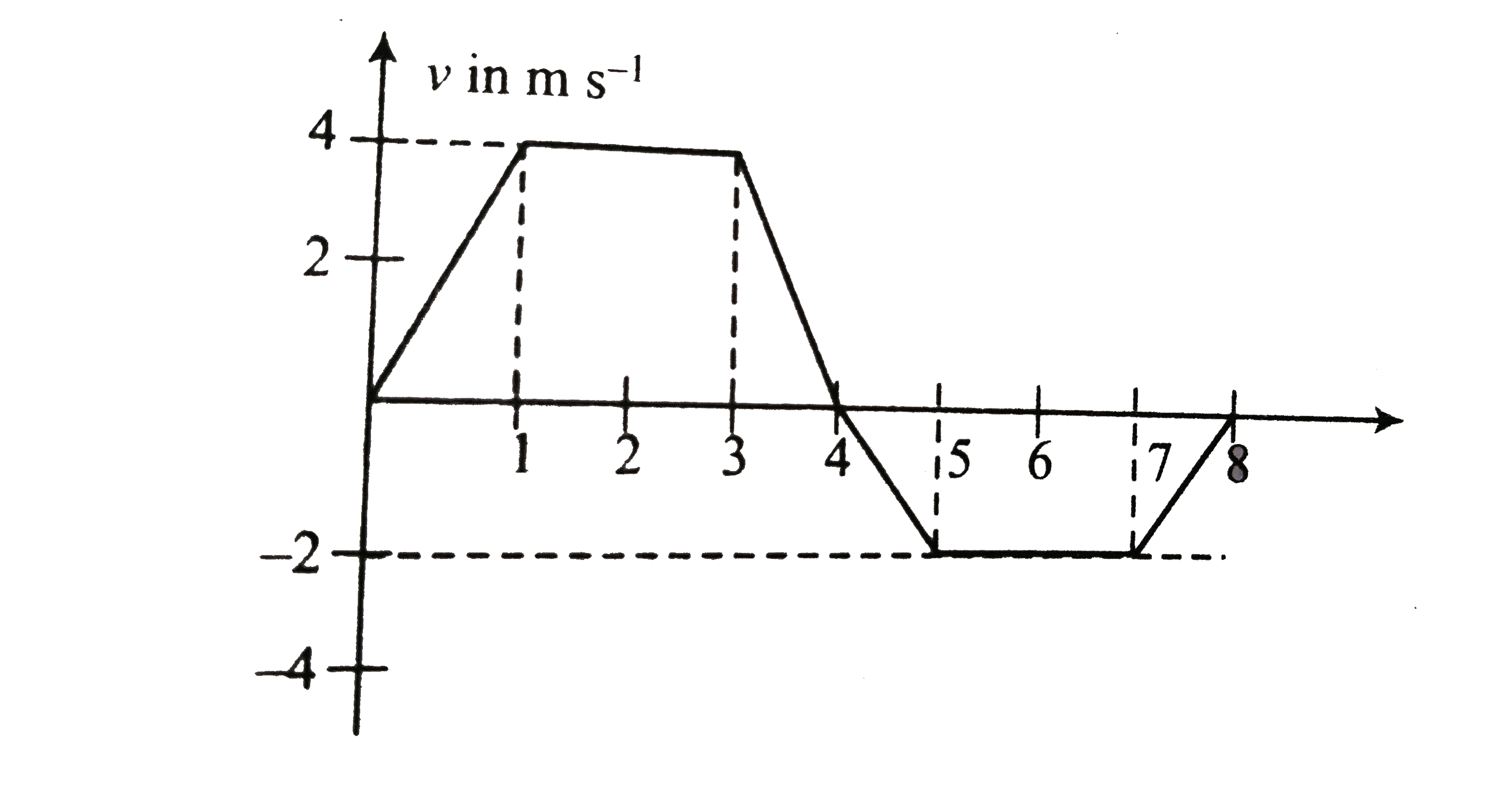 .
.
The distance of the particle from the origin after 8s is .
View SolutionVelocity of a particle varies as v=2t3−3t2 in kmhr If t=0 is taken at 12:00 noon
Q. What is the velocity of the particle at 12:00 noon?
View SolutionThe position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleration of particle varies with time as shown.

(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.
View Solution
