The velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.
3ms−2
4ms−2
3.5ms−2
5ms−2
The correct Answer is:A
To find the magnitude of the maximum acceleration of the particle given the velocity as v=√9−x2m/s, we can follow these steps:
Step 1: Express acceleration in terms of displacement
The acceleration a can be expressed as:
a=dvdt
Using the chain rule, we can write:
a=dvdx⋅dxdt=vdvdx
Step 2: Differentiate the velocity function
Given v=√9−x2, we first differentiate v with respect to x:
v2=9−x2
Differentiating both sides with respect to x:
2vdvdx=−2x
From this, we can isolate dvdx:
dvdx=−xv
Step 3: Substitute back to find acceleration
Now substituting dvdx back into the expression for acceleration:
a=v⋅dvdx=v⋅(−xv)=−x
Thus, the acceleration is:
a=−x
Step 4: Find the maximum magnitude of acceleration
The magnitude of acceleration is given by:
|a|=|x|
From the velocity equation v=√9−x2, we know that 9−x2≥0, which implies:
x2≤9⇒|x|≤3
Thus, the maximum value of |x| is 3.
Step 5: Conclusion
Therefore, the maximum magnitude of acceleration is:
|a|max=3m/s2
Final Answer
The magnitude of the maximum acceleration of the particle is 3m/s2.
---
The acceleration a can be expressed as:
a=dvdt
Using the chain rule, we can write:
a=dvdx⋅dxdt=vdvdx
Given v=√9−x2, we first differentiate v with respect to x:
v2=9−x2
Differentiating both sides with respect to x:
2vdvdx=−2x
From this, we can isolate dvdx:
dvdx=−xv
Now substituting dvdx back into the expression for acceleration:
a=v⋅dvdx=v⋅(−xv)=−x
Thus, the acceleration is:
a=−x
The magnitude of acceleration is given by:
|a|=|x|
From the velocity equation v=√9−x2, we know that 9−x2≥0, which implies:
x2≤9⇒|x|≤3
Thus, the maximum value of |x| is 3.
Therefore, the maximum magnitude of acceleration is:
|a|max=3m/s2
The magnitude of the maximum acceleration of the particle is 3m/s2.
Similar Questions
If the displacement of a particle varies with time as √x=t+3
View SolutionThe velocity of any particle is related with its displacement As, x=√v+1, Calculate acceleration at x=5m.
View SolutionVelocity of a particle varies as v=2t3−3t2 in kmhr If t=0 is taken at 12:00 noon
Q. Find the expression for the acceleration of the particle.
View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionThe velocity of a particle is given by v=(2t2−3t+10)ms−1. Find the instantaneous acceleration at t = 5 s.
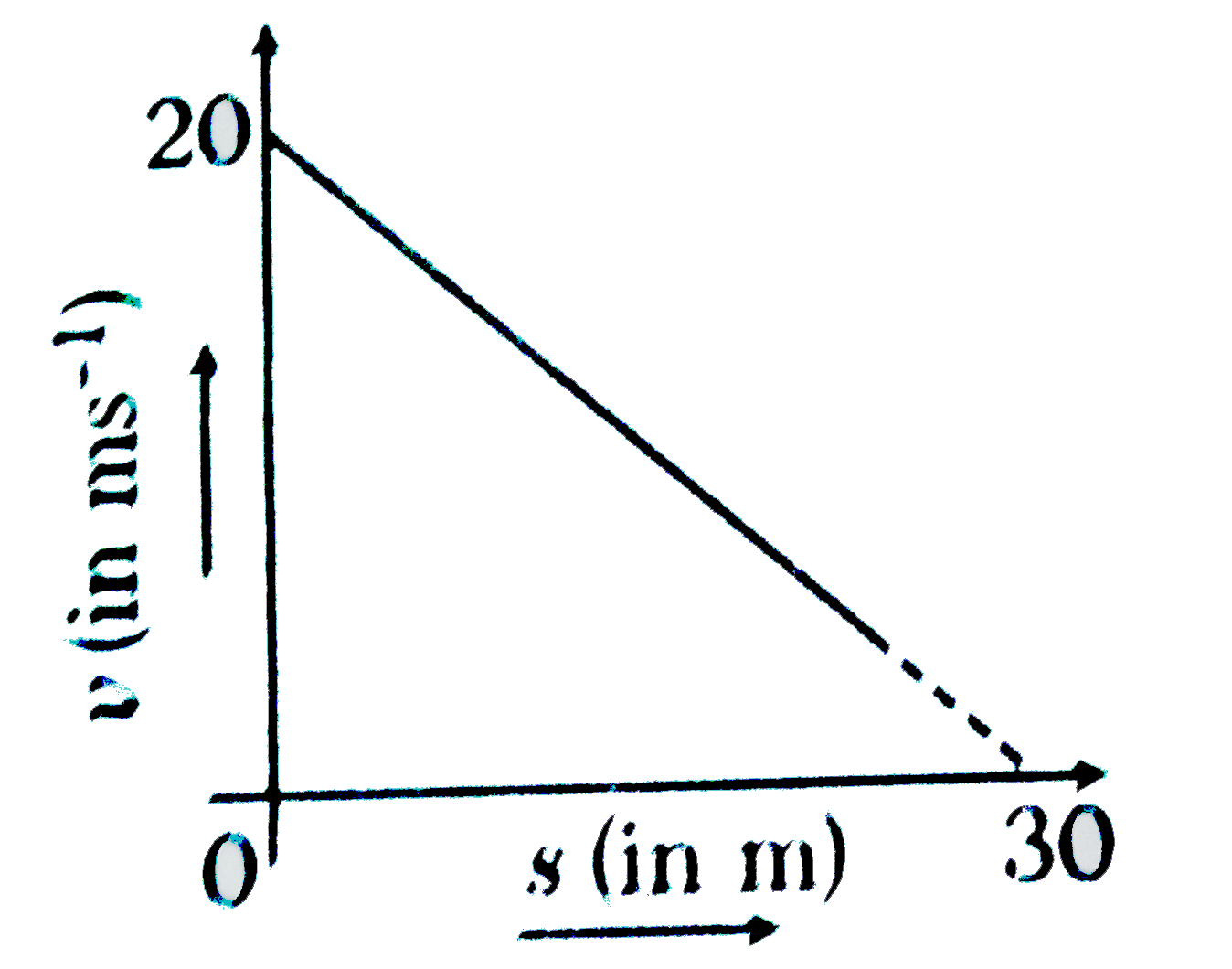
View SolutionIf the velocity v of particle moving along a straight line decreases linearly with its displacement s from 20ms−1 to a value approaching zero at s = 30 m, then acceleration of the particle at v=10ms^(-1) is
View SolutionIf the displacement of a particle varies with time as x=5t2+7t.
Then find its velocity.
View SolutionThe velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
View SolutionVelocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
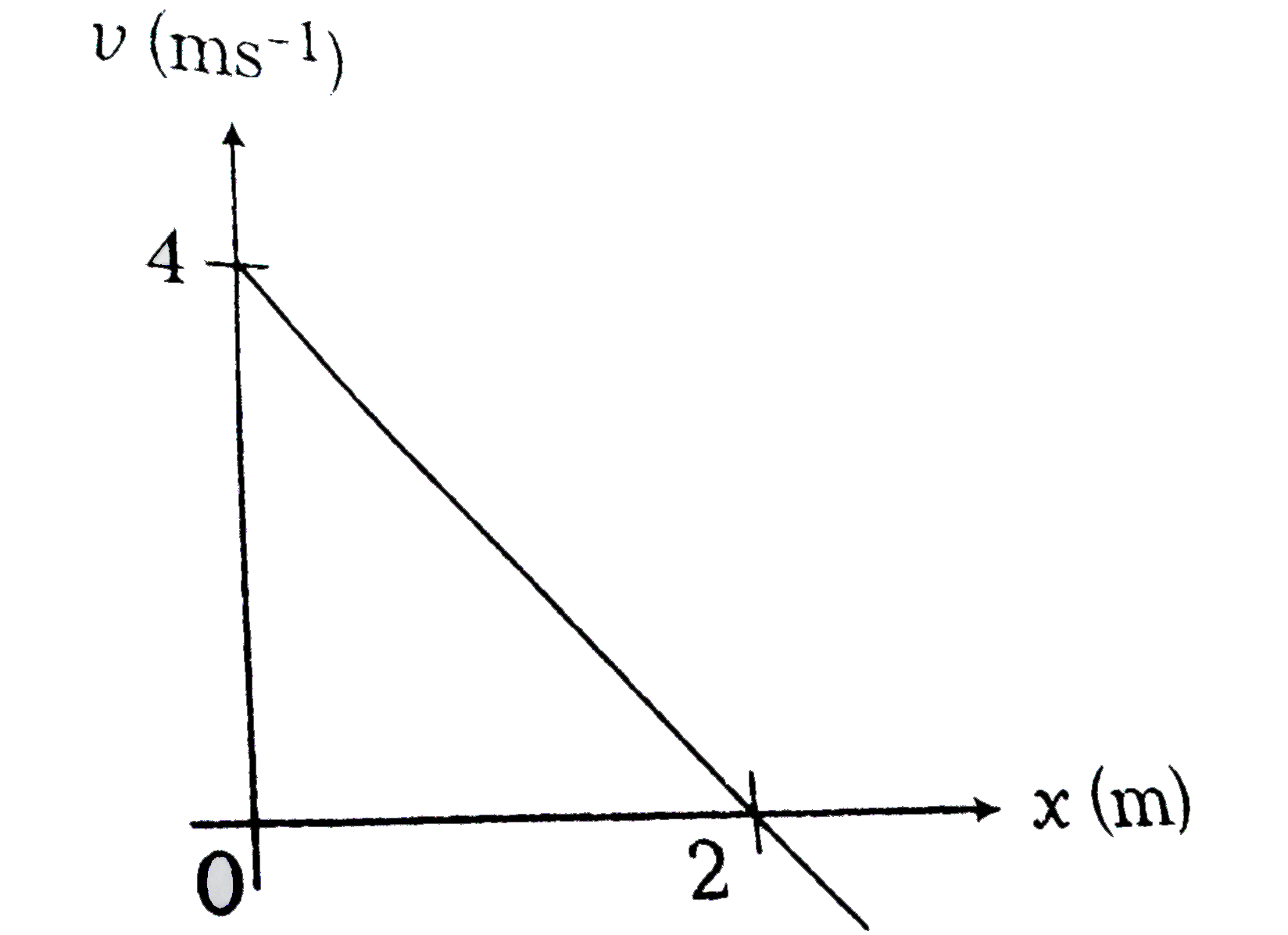
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
View Solution
