A particle P lying on a smooth horizontal x−y plane starts from (3ˆi+4ˆj)m with velocity (2ˆi)m/s. Another particle Q is projected (horizontally from origin with velocity (xˆi+yˆj) so that is strikes P after 2s. Then
x=2.0
x=3.5
y=2.0
y=3.5
The correct Answer is:B, C
To solve the problem step by step, we will analyze the motion of both particles P and Q.
Step 1: Determine the final position of particle P
- Particle P starts at position (3^i+4^j) meters and moves with a velocity of (2^i) m/s.
- The time of motion is 2 seconds.
- The displacement of P can be calculated using the formula:
Displacement=Velocity×Time=(2^i)×2=4^i meters
- Therefore, the final position of particle P after 2 seconds is:
Final Position of P=(3^i+4^j)+4^i=(3+4)^i+4^j=7^i+4^j meters
Step 2: Determine the final position of particle Q
- Particle Q is projected horizontally from the origin (0^i+0^j) with a velocity of (x^i+y^j).
- The position of Q after 2 seconds can be calculated as:
Final Position of Q=(x^i+y^j)×2=(2x^i+2y^j) meters
Step 3: Set the final positions equal
- Since both particles strike each other after 2 seconds, their final positions must be equal:
7^i+4^j=2x^i+2y^j
Step 4: Equate the coefficients
- By equating the coefficients of ^i and ^j:
1. For ^i:
2x=7⟹x=72=3.5
2. For ^j:
2y=4⟹y=42=2
Conclusion
- The values of x and y are:
x=3.5,y=2
- Particle P starts at position (3^i+4^j) meters and moves with a velocity of (2^i) m/s.
- The time of motion is 2 seconds.
- The displacement of P can be calculated using the formula:
Displacement=Velocity×Time=(2^i)×2=4^i meters
- Therefore, the final position of particle P after 2 seconds is:
Final Position of P=(3^i+4^j)+4^i=(3+4)^i+4^j=7^i+4^j meters
- Particle Q is projected horizontally from the origin (0^i+0^j) with a velocity of (x^i+y^j).
- The position of Q after 2 seconds can be calculated as:
Final Position of Q=(x^i+y^j)×2=(2x^i+2y^j) meters
- Since both particles strike each other after 2 seconds, their final positions must be equal:
7^i+4^j=2x^i+2y^j
- By equating the coefficients of ^i and ^j:
1. For ^i:
2x=7⟹x=72=3.5
2. For ^j:
2y=4⟹y=42=2
- The values of x and y are:
x=3.5,y=2
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
View SolutionA particle P is at the origin starts with velocity u=(2ˆi−4ˆj)m/s with constant acceleration (3ˆi+5ˆj)m/s2. After travelling for 2s its distance from the origin is
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionAcceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionA particle is projected from ground with velocity 50m/s at 37∘ from horizontal. Find velocity and displacement after 2 s. sin37∘=35.
View SolutionTwo inclined planes OA and OB intersect in a horizontal plane having their inclinations αandβ with the horizontal as shown in figure. A particle is projected from P with velocity u along a direction perpendicular to plane OA. The particle strikes plane OB perpendicularly at Q.
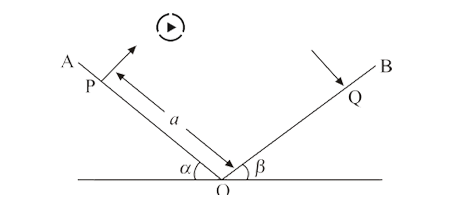
The path of the particle from P to Q is
View SolutionA particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
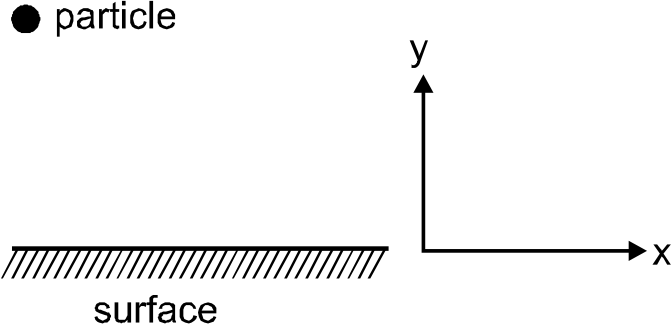
View SolutionA particle moving with velocity (2ˆi−3ˆj) m/s collides with a surface at rest in xz–plane as shown in figure and moves with velocity (2ˆi+2ˆj) m/s after collision. Then coefficient of restitution is :
View SolutionVelocity of a particle changes from (3ˆi+4ˆj)m/s to (6ˆi+5ˆj)m/s 2s. Find magnitude and direction of average acceleration.
View SolutionA body is projected with a initial velocity of (8ˆi+6ˆj)ms−1 . The horizontal range is (g=10ms−2)
View Solution
