Two smooth spheres and of masses and move with velocities and in opposite directions. If rebounds on its path with velocity , then
The velocity of sphere after the impact
The coefficient of impact
The loss of kinetic energy
Impulse by on is
To solve the problem step by step, we will analyze the situation involving two spheres A and B, their masses, initial velocities, and the final velocity of sphere A after the collision. We will use the principles of conservation of momentum and kinetic energy to find the required quantities.
Step 1: Define the Given Data
- Mass of sphere A, mA=4kg
- Mass of sphere B, mB=8kg
- Initial velocity of sphere A, vA=9m/s (to the right)
- Initial velocity of sphere B, vB=−3m/s (to the left, hence negative)
- Final velocity of sphere A after collision, v′A=−1m/s (since it rebounds)
Step 2: Calculate Initial Momentum
The initial momentum pinitial of the system can be calculated using the formula:
pinitial=mA⋅vA+mB⋅vB
Substituting the values:
pinitial=(4kg⋅9m/s)+(8kg⋅−3m/s)=36kg m/s−24kg m/s=12kg m/s
Step 3: Set Up the Equation for Final Momentum
Let the final velocity of sphere B be v′B. The final momentum pfinal is given by:
pfinal=mA⋅v′A+mB⋅v′B
Substituting the known values:
pfinal=(4kg⋅−1m/s)+(8kg⋅v′B)
pfinal=−4kg m/s+8kg⋅v′B
Step 4: Apply Conservation of Momentum
According to the conservation of momentum:
pinitial=pfinal
Thus, we have:
12kg m/s=−4kg m/s+8kg⋅v′B
Rearranging gives:
8kg⋅v′B=12+4=16
v′B=168=2m/s
Step 5: Calculate the Coefficient of Restitution
The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- Velocity of separation = v′B−v′A=2−(−1)=2+1=3m/s
- Velocity of approach = vA−vB=9−(−3)=9+3=12m/s
Thus,
e=312=14
Step 6: Calculate the Impulse on Each Sphere
Impulse J is the change in momentum. For sphere B:
JB=mB(v′B−vB)=8kg⋅(2−(−3))=8⋅(2+3)=8⋅5=40Ns
For sphere A:
JA=mA(v′A−vA)=4kg⋅(−1−9)=4⋅(−10)=−40Ns
Step 7: Calculate Change in Kinetic Energy
Initial kinetic energy KEinitial:
KEinitial=12mAv2A+12mBv2B=12⋅4⋅92+12⋅8⋅32
=2⋅81+4⋅9=162+36=198J
Final kinetic energy KEfinal:
KEfinal=12mA(v′A)2+12mB(v′B)2=12⋅4⋅(−1)2+12⋅8⋅(2)2
=2⋅1+4⋅4=2+16=18J
Change in kinetic energy:
ΔKE=KEfinal−KEinitial=18−198=−180J
Summary of Results
- Final velocity of B: v′B=2m/s
- Coefficient of restitution: e=14
- Impulse on B: JB=40Ns
- Change in kinetic energy: ΔKE=−180J
- Mass of sphere A, mA=4kg
- Mass of sphere B, mB=8kg
- Initial velocity of sphere A, vA=9m/s (to the right)
- Initial velocity of sphere B, vB=−3m/s (to the left, hence negative)
- Final velocity of sphere A after collision, v′A=−1m/s (since it rebounds)
The initial momentum pinitial of the system can be calculated using the formula:
pinitial=mA⋅vA+mB⋅vB
Substituting the values:
pinitial=(4kg⋅9m/s)+(8kg⋅−3m/s)=36kg m/s−24kg m/s=12kg m/s
Let the final velocity of sphere B be v′B. The final momentum pfinal is given by:
pfinal=mA⋅v′A+mB⋅v′B
Substituting the known values:
pfinal=(4kg⋅−1m/s)+(8kg⋅v′B)
pfinal=−4kg m/s+8kg⋅v′B
According to the conservation of momentum:
pinitial=pfinal
Thus, we have:
12kg m/s=−4kg m/s+8kg⋅v′B
Rearranging gives:
8kg⋅v′B=12+4=16
v′B=168=2m/s
The coefficient of restitution e is defined as:
e=Velocity of separationVelocity of approach
- Velocity of separation = v′B−v′A=2−(−1)=2+1=3m/s
- Velocity of approach = vA−vB=9−(−3)=9+3=12m/s
e=312=14
Impulse J is the change in momentum. For sphere B:
JB=mB(v′B−vB)=8kg⋅(2−(−3))=8⋅(2+3)=8⋅5=40Ns
JA=mA(v′A−vA)=4kg⋅(−1−9)=4⋅(−10)=−40Ns
Initial kinetic energy KEinitial:
KEinitial=12mAv2A+12mBv2B=12⋅4⋅92+12⋅8⋅32
=2⋅81+4⋅9=162+36=198J
KEfinal=12mA(v′A)2+12mB(v′B)2=12⋅4⋅(−1)2+12⋅8⋅(2)2
=2⋅1+4⋅4=2+16=18J
ΔKE=KEfinal−KEinitial=18−198=−180J
- Final velocity of B: v′B=2m/s
- Coefficient of restitution: e=14
- Impulse on B: JB=40Ns
- Change in kinetic energy: ΔKE=−180J
Topper's Solved these Questions
Similar Questions
A body of mass 2kg moving with a velocity 3m/s collides with a body of mass 1kg moving with a velocity of 4m/s in opposite direction. If the collision is head on and completely inelastic, then
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View SolutionA thin ring of mass 2kg and radius 0.5 m is rolling without on a horizontal plane with velocity 1m/s. A small ball of mass 0.1kg, moving with velocity 20 m/s in the opposite direction hits the ring at a height of 0.75m and goes vertically up with velocity 10m/s. Immediately after the collision

View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then

View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
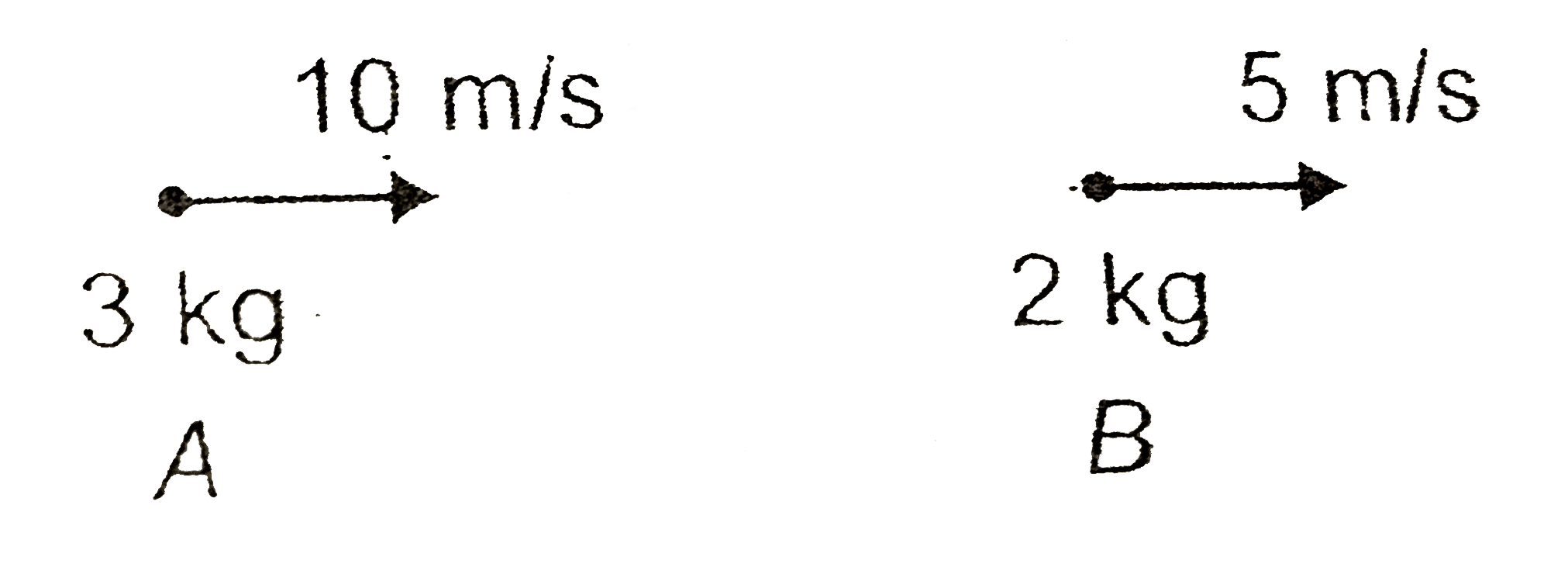
Find the maximum momentum that particle B can have after collision with A
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
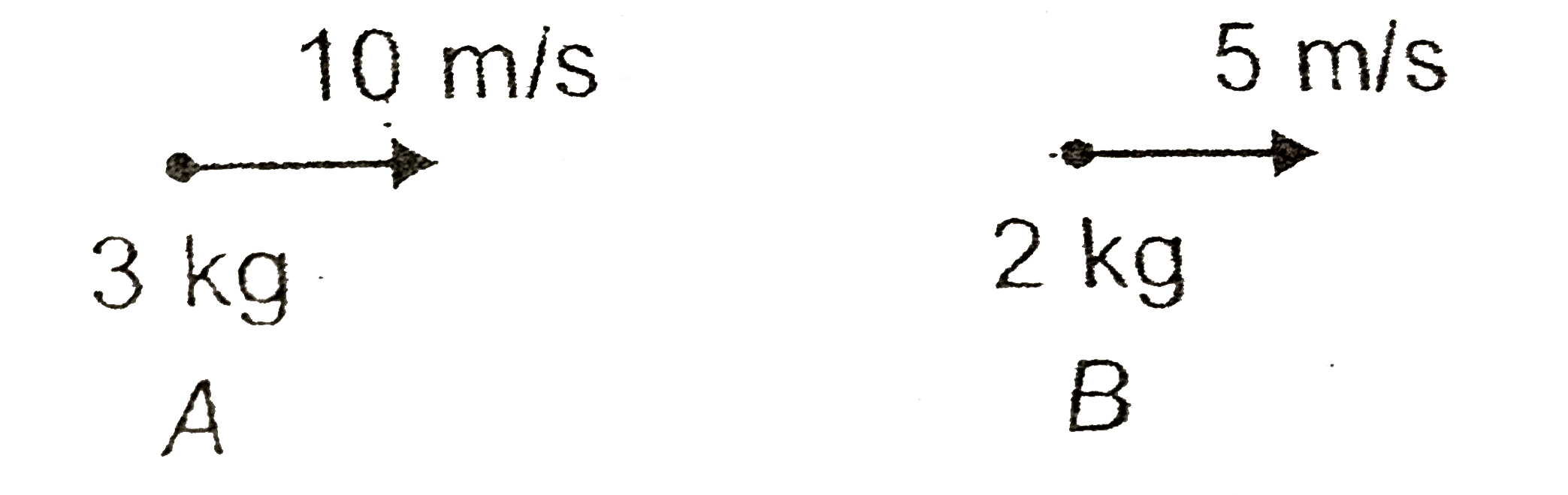
Kinetic energy of particle A when particle B has the maximum momentum
View SolutionTwo balls of masses 2kg and 4kg are moved towards each other with velocities 4m/s and 2m/s, respectively, on a frictionless surface. After colliding, the 2kg ball returns back with velocity 2m/s. then find
a. velocity of the 4kg after collision
b. coefficient of restitution e,
c. impulse of deformation JD
d. maximum potential energy of deformation,
e. impulse of reformation JR
View SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
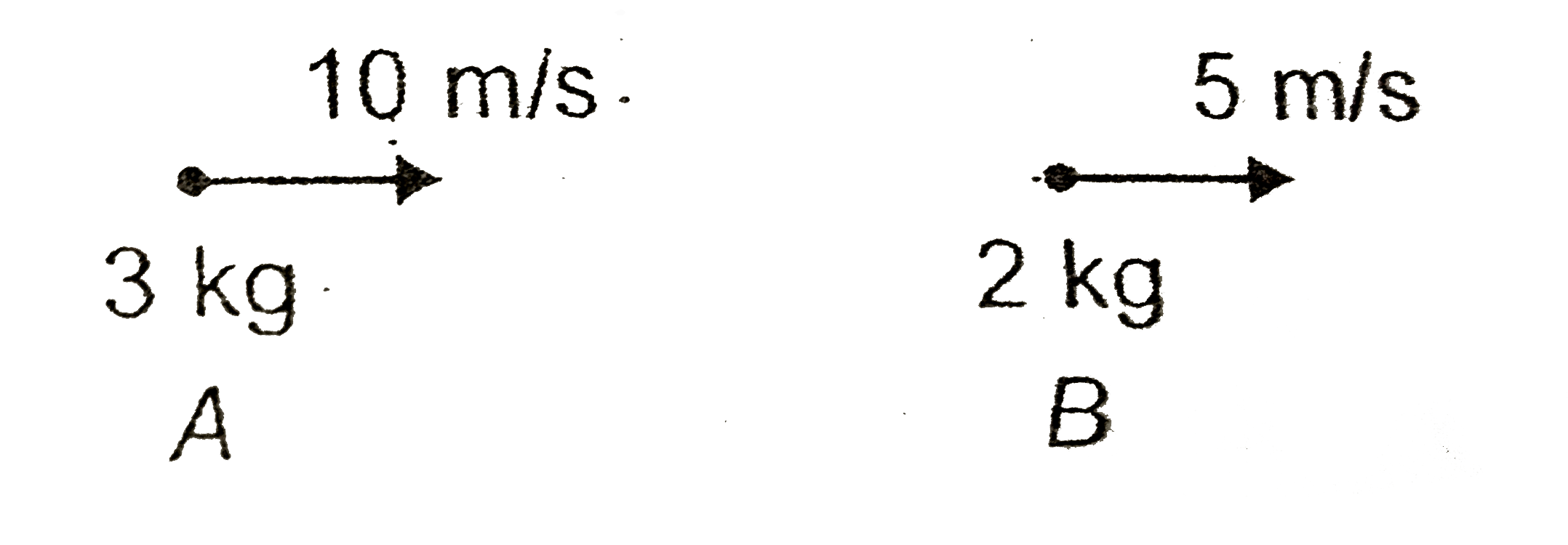
Find the maximum momentum that particles A can have after collision with B.
View SolutionA small sphere of mass m=1kg is moving with a velocity (4ˆi−ˆj)m/s. it hits a fixed smooth wall and rebounds with velocity (ˆi+3ˆj)m/s. The coefficient of restitution between the sphere and the wall is n/16. Find the value of n.
View SolutionA ball of mass 4kg moving with a velocity of 12m/s impinges directly on another ball of mass 8kg moving with velocity of 4m/s in the same direction. Find their velocities after impact and calculate the loss of KE due to impact if e=0.5.
View Solution
