The potential difference across the terminals of a battery is 10 V when there is a current of 3 A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
2.5Ω
5.0Ω
2.83Ω
1Ω
The correct Answer is:D
To find the internal resistance of the battery, we can use the information provided in the question. We will set up equations based on the potential differences and the currents given.
1. Understanding the Problem:
- We have two scenarios with different currents and potential differences.
- Let E be the electromotive force (emf) of the battery and r be the internal resistance.
2. First Scenario:
- When the current I1=3A flows from negative to positive terminal, the potential difference Vpq=10V.
- According to Kirchhoff's law, we can write:
Vpq=E−I1r
- Substituting the known values:
10=E−3r(Equation 1)
3. Second Scenario:
- When the current I2=2A flows in the reverse direction, the potential difference Vpq=15V.
- Again, applying Kirchhoff's law:
Vpq=E+I2r
- Substituting the known values:
15=E+2r(Equation 2)
4. Solving the Equations:
- We have the two equations:
1. 10=E−3r
2. 15=E+2r
- From Equation 1, we can express E:
E=10+3r(Substituting into Equation 2)
- Substitute E into Equation 2:
15=(10+3r)+2r
15=10+5r
5=5r
r=1Ω
5. Finding the Value of E:
- Now substitute r=1Ω back into Equation 1 to find E:
E=10+3(1)=13V
Final Answer:
- The internal resistance of the battery is r=1Ω and the emf E=13V.
- We have two scenarios with different currents and potential differences.
- Let E be the electromotive force (emf) of the battery and r be the internal resistance.
- When the current I1=3A flows from negative to positive terminal, the potential difference Vpq=10V.
- According to Kirchhoff's law, we can write:
Vpq=E−I1r
- Substituting the known values:
10=E−3r(Equation 1)
- When the current I2=2A flows in the reverse direction, the potential difference Vpq=15V.
- Again, applying Kirchhoff's law:
Vpq=E+I2r
- Substituting the known values:
15=E+2r(Equation 2)
- We have the two equations:
1. 10=E−3r
2. 15=E+2r
E=10+3r(Substituting into Equation 2)
15=(10+3r)+2r
15=10+5r
5=5r
r=1Ω
- Now substitute r=1Ω back into Equation 1 to find E:
E=10+3(1)=13V
- The internal resistance of the battery is r=1Ω and the emf E=13V.
Topper's Solved these Questions
Similar Questions
The potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View SolutionPotential difference across the terminal of a non ideal battery is
View Solution
Knowledge Check
When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 12 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 15 V, the emf of the battery is
A12.6VB13.2VC13.5VD14.0V
Potential different across the terminals of the battery shown in figure is
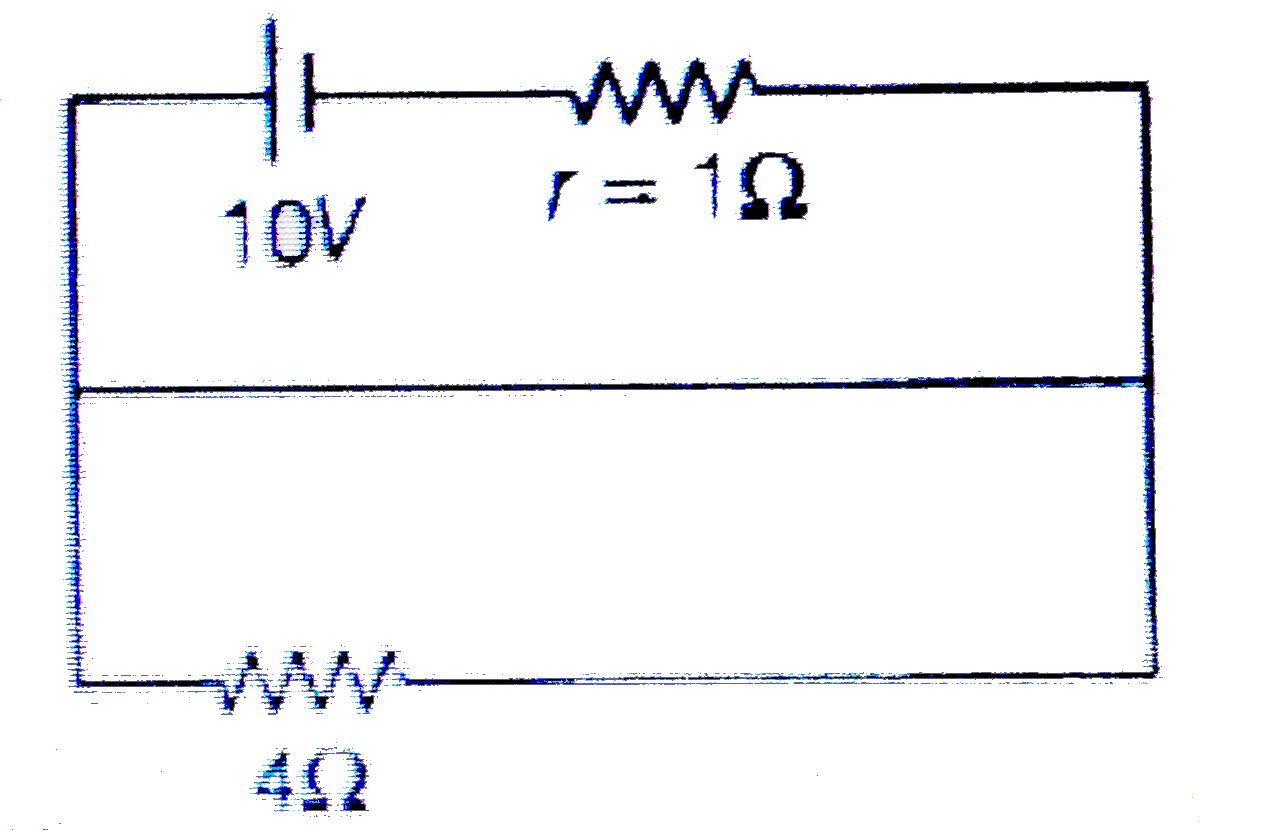
View SolutionThe potential difference between the terminals of a 6.0V battery is 7.2 V when it is being charged by a current of 2.0A.What is the internal resistance of the battery?
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
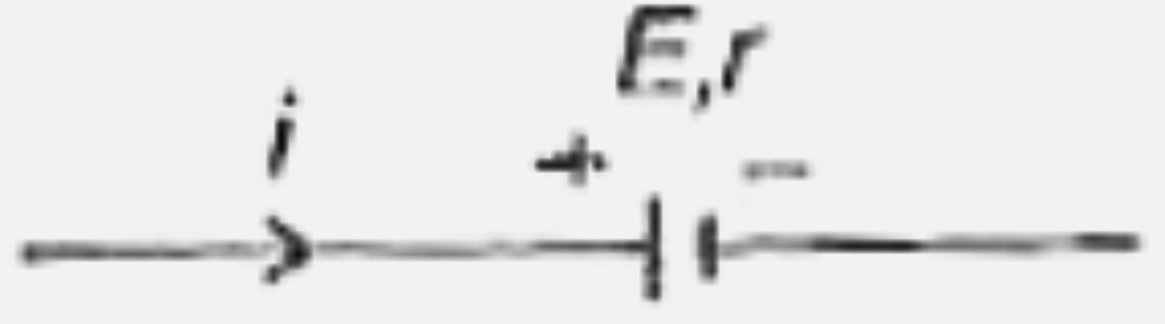
View SolutionThe potential difference between the terminals of an electric heater is 60V when it draws a current of 4A from the source. What current will the heater draw if the potential difference is increased to 120V ?
View SolutionWhen current supplied by a cell to a circuit is 0.3A, its terminal potential difference is 0.9 A. When the current supplied becomes 0.2 A, its terminal potential difference becomes 1.0 V . The internal resistance of the cell is
View SolutionA voltmeter reads the potential difference across the terminals of an old battery as 1.40V, while a potentiometer reads its voltage to be 1.55V. The voltmeter resistance is 280Ω.
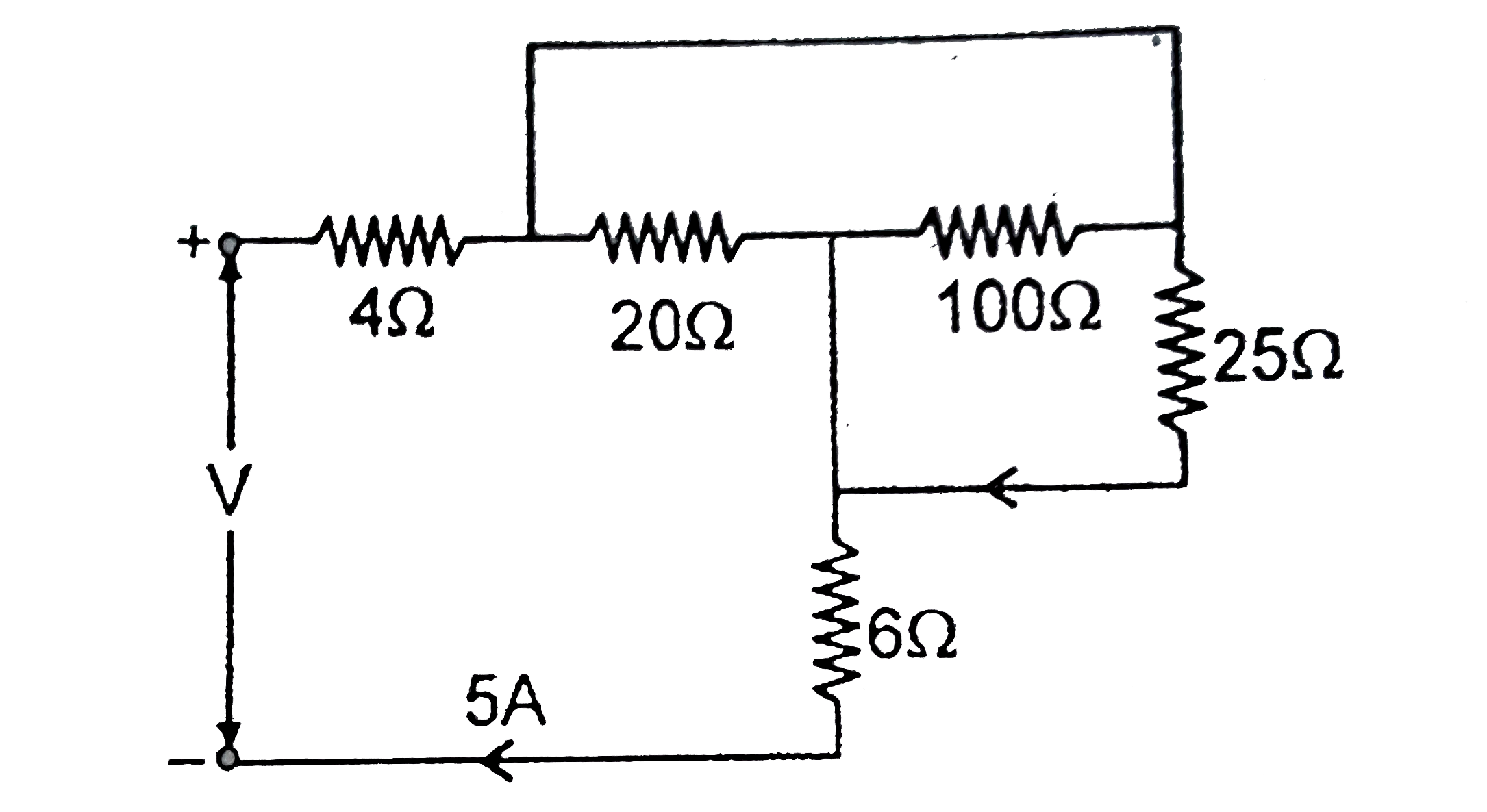
View SolutionIn the circuit, V is potential differences across the terminal as shwon in figure. Then the value of V is
View Solution
