n identical cells are joined in series with two cells A and B with reversed polarities. EMF of each cell is E and internal resistance is r. Potential difference across cell A or B is (n > 4)
2En
2E(1−1n)
4En
2E(1−2n)
The correct Answer is:D
To solve the problem of finding the potential difference across cell A or B when n identical cells are joined in series with two cells A and B with reversed polarities, we can follow these steps:
1. Understand the Configuration:
- We have n identical cells in series, each with an EMF of E and an internal resistance of r.
- There are two additional cells A and B connected in reverse polarity.
2. Calculate the Total EMF:
- The total EMF contributed by the n cells is nE.
- The two cells A and B in reverse polarity will neutralize 2E from the total EMF.
- Therefore, the effective EMF in the circuit is given by:
\(
E_{\text{total}} = nE - 2E = (n - 2)E
\)
3. Calculate the Total Internal Resistance:
- The total internal resistance from the n cells is nr.
- The internal resistances of cells A and B are not specified, so we assume they are negligible or included in the total resistance.
4. Find the Current (I):
- Using Ohm's law, the current I flowing through the circuit can be calculated as:
\(
I = \frac{E_{\text{total}}}{R_{\text{total}}} = \frac{(n - 2)E}{nr}
\)
5. Calculate the Potential Difference Across Cell A:
- The potential difference across cell A can be calculated using the formula:
\(
\Delta V_A = E + I \cdot r
\)
- Substituting the value of I into the equation:
\(
\Delta V_A = E + \left(\frac{(n - 2)E}{nr}\right) \cdot r
\)
- Simplifying this gives:
\(
\Delta V_A = E + \frac{(n - 2)E}{n} = E + \frac{(n - 2)E}{n}
\)
6. Combine the Terms:
- Combine the terms to find a common expression:
\(
\Delta V_A = \frac{nE}{n} + \frac{(n - 2)E}{n} = \frac{nE + (n - 2)E}{n} = \frac{(2n - 2)E}{n}
\)
7. Final Expression:
- Factor out the common terms:
\(
\Delta V_A = \frac{2E(n - 1)}{n}
\)
Final Answer:
The potential difference across cell A (or B) is:
\(
\Delta V_A = \frac{2E(n - 1)}{n}
\)
- We have n identical cells in series, each with an EMF of E and an internal resistance of r.
- There are two additional cells A and B connected in reverse polarity.
- The total EMF contributed by the n cells is nE.
- The two cells A and B in reverse polarity will neutralize 2E from the total EMF.
- Therefore, the effective EMF in the circuit is given by:
\(
E_{\text{total}} = nE - 2E = (n - 2)E
\)
- The total internal resistance from the n cells is nr.
- The internal resistances of cells A and B are not specified, so we assume they are negligible or included in the total resistance.
- Using Ohm's law, the current I flowing through the circuit can be calculated as:
\(
I = \frac{E_{\text{total}}}{R_{\text{total}}} = \frac{(n - 2)E}{nr}
\)
- The potential difference across cell A can be calculated using the formula:
\(
\Delta V_A = E + I \cdot r
\)
- Substituting the value of I into the equation:
\(
\Delta V_A = E + \left(\frac{(n - 2)E}{nr}\right) \cdot r
\)
- Simplifying this gives:
\(
\Delta V_A = E + \frac{(n - 2)E}{n} = E + \frac{(n - 2)E}{n}
\)
- Combine the terms to find a common expression:
\(
\Delta V_A = \frac{nE}{n} + \frac{(n - 2)E}{n} = \frac{nE + (n - 2)E}{n} = \frac{(2n - 2)E}{n}
\)
- Factor out the common terms:
\(
\Delta V_A = \frac{2E(n - 1)}{n}
\)
The potential difference across cell A (or B) is:
\(
\Delta V_A = \frac{2E(n - 1)}{n}
\)
Topper's Solved these Questions
Similar Questions
n identical cells are joined in series with two cells A and B with reversed polarities. EMF of each cell is E and internal resistance is r. Potential difference across cell A or B is (n gt 4)
View SolutionA capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View Solution
Knowledge Check
Two cells e1ande2 connected in opposition to each other as shown in figure. The cell of emf 9 V and internal resistance 3Ω the cell is of emf 7V and internal resistance 7Ω. The potential difference between the points A and B is
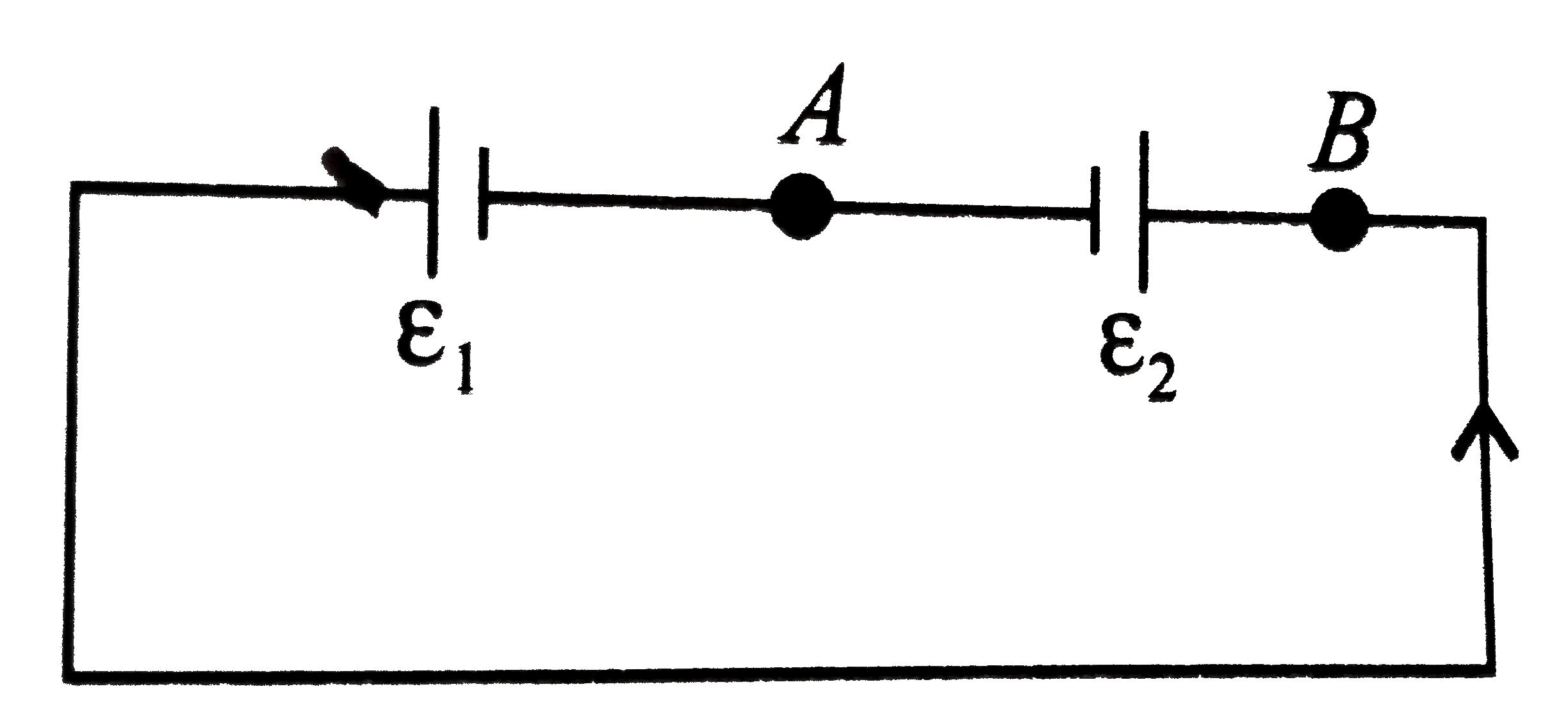 A8.4VB5.6VC7.8VD6.6V
A8.4VB5.6VC7.8VD6.6V
In the situation shown , the potential difference across the cell of smaller e.m.f is .
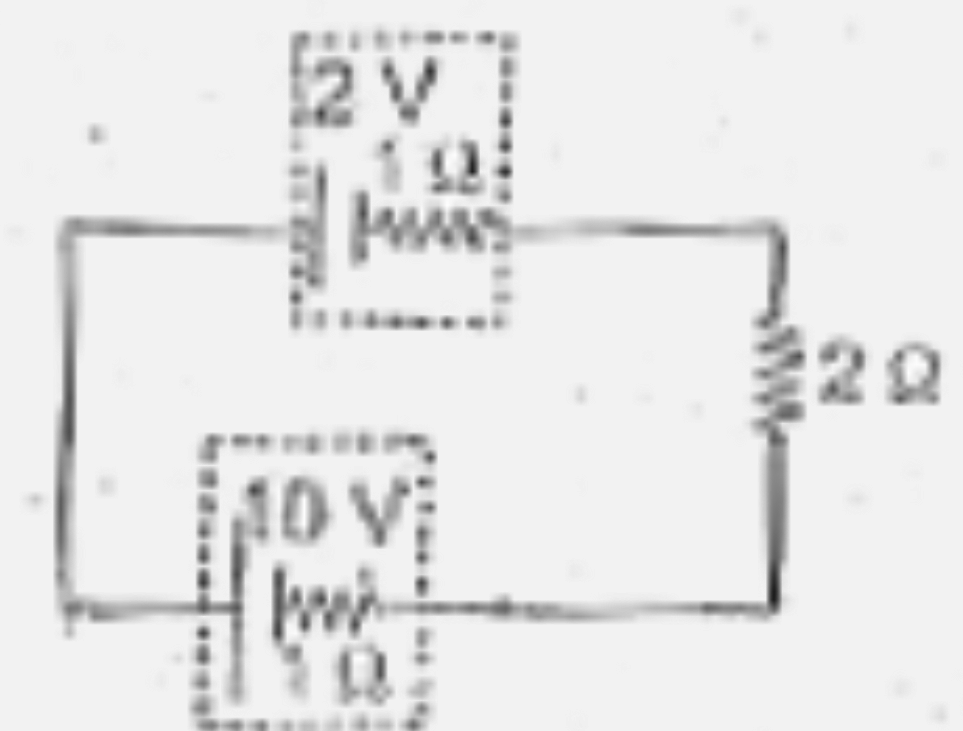
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionIn the situation shown , The potential difference across the cell of smaller e.m.f. is

View SolutionN identical cells whether joined together in series or in parallel, give the same current, when connected to an external resistance of 'R'. The internal resistance of each cell is:-
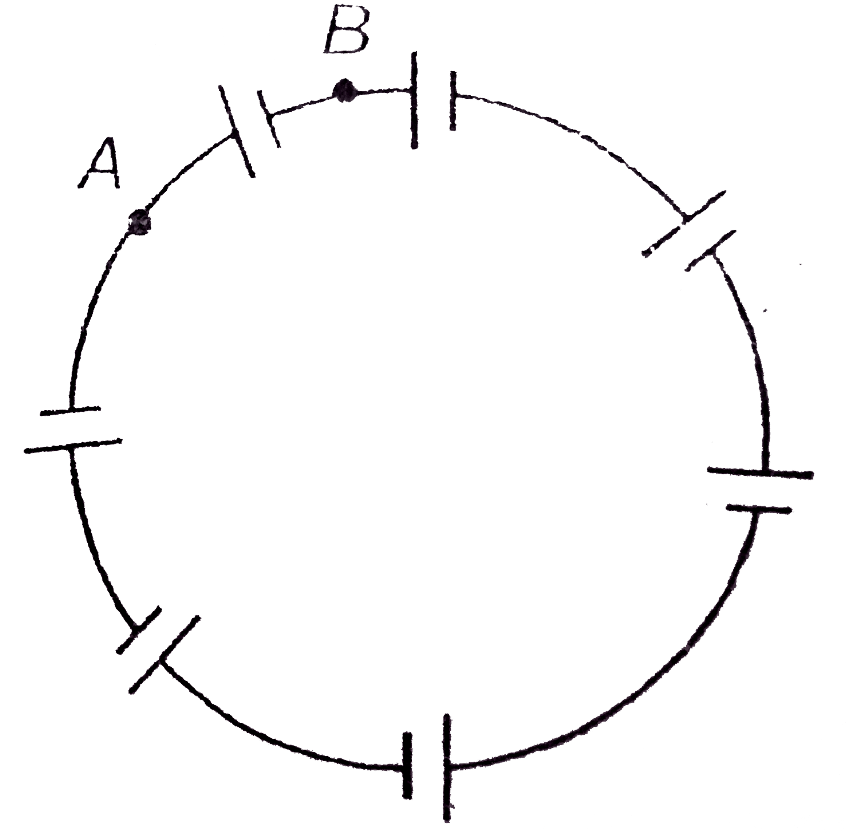
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
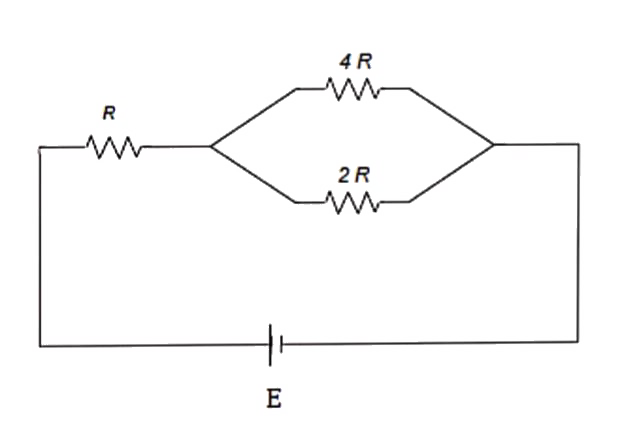
View SolutionThe figure shows a network in which the cell is deal and it has an emf E. The potential difference across the resistance 2R is
View SolutionFour cells each of emf E and internal resistance r are connected in series to form a loop ABCD. Find potential difference across (1) AB, (2) AC
View Solution
