Three rods of identical cross-sectional area and made from the same metal form the sides of an equilateral triangle ABC The points A and B are maintained at temperature √3T and T respectively In the steady state, the temperature of the point C is TC Assuming that only heat conduction takes place, the value of TC/T is equal to .
1+√32
1−√32
1+√22
1−√22
The correct Answer is:A
To solve the problem, we need to analyze the heat conduction in the three rods forming an equilateral triangle. The rods are denoted as AB, BC, and CA, and we know the temperatures at points A and B, as well as the temperature at point C (which we will denote as TC).
1. Identify the Given Temperatures:
- Temperature at point A: TA=√3T
- Temperature at point B: TB=T
- Temperature at point C: TC (unknown)
2. Understand the Heat Conduction:
- In a steady state, the rate of heat conduction through each rod must be equal. The heat conduction can be expressed as:
TA−TCRCA=TC−TBRBC
- Here, RCA and RBC are the thermal resistances of rods CA and BC, respectively.
3. Calculate the Thermal Resistances:
- The thermal resistance R for a rod can be expressed as:
R=LkA
- Since all rods have the same length L, area A, and are made of the same material (same thermal conductivity k), we have:
RCA=RBC=LkA
4. Set Up the Equation:
- Using the thermal resistances, we can rewrite the heat conduction equation:
√3T−TCLkA=TC−TLkA
- The LkA cancels out from both sides:
√3T−TC=TC−T
5. Rearranging the Equation:
- Rearranging gives:
√3T−T=2TC
- This simplifies to:
TC=√3T−T2=(√3−1)T2
6. Finding the Ratio TCT:
- Now, we can express the ratio:
TCT=(√3−1)T2T=√3−12
7. Final Result:
- Therefore, the value of TCT is:
TCT=√3−12
- Temperature at point A: TA=√3T
- Temperature at point B: TB=T
- Temperature at point C: TC (unknown)
- In a steady state, the rate of heat conduction through each rod must be equal. The heat conduction can be expressed as:
TA−TCRCA=TC−TBRBC
- Here, RCA and RBC are the thermal resistances of rods CA and BC, respectively.
- The thermal resistance R for a rod can be expressed as:
R=LkA
- Since all rods have the same length L, area A, and are made of the same material (same thermal conductivity k), we have:
RCA=RBC=LkA
- Using the thermal resistances, we can rewrite the heat conduction equation:
√3T−TCLkA=TC−TLkA
- The LkA cancels out from both sides:
√3T−TC=TC−T
- Rearranging gives:
√3T−T=2TC
- This simplifies to:
TC=√3T−T2=(√3−1)T2
- Now, we can express the ratio:
TCT=(√3−1)T2T=√3−12
- Therefore, the value of TCT is:
TCT=√3−12
Topper's Solved these Questions
Similar Questions
Three rods of identical area of cross-section and made from the same metal from the sides of an isosceles triangle. ABC, right angled at B. The points A and B are maintained at temperatures T and √2T RESPECTIVELY. In the steady state the temperature of the point C is TC.
Assuming that only heat conduction takes place , TCT is equal to
View SolutionThree rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be

View Solution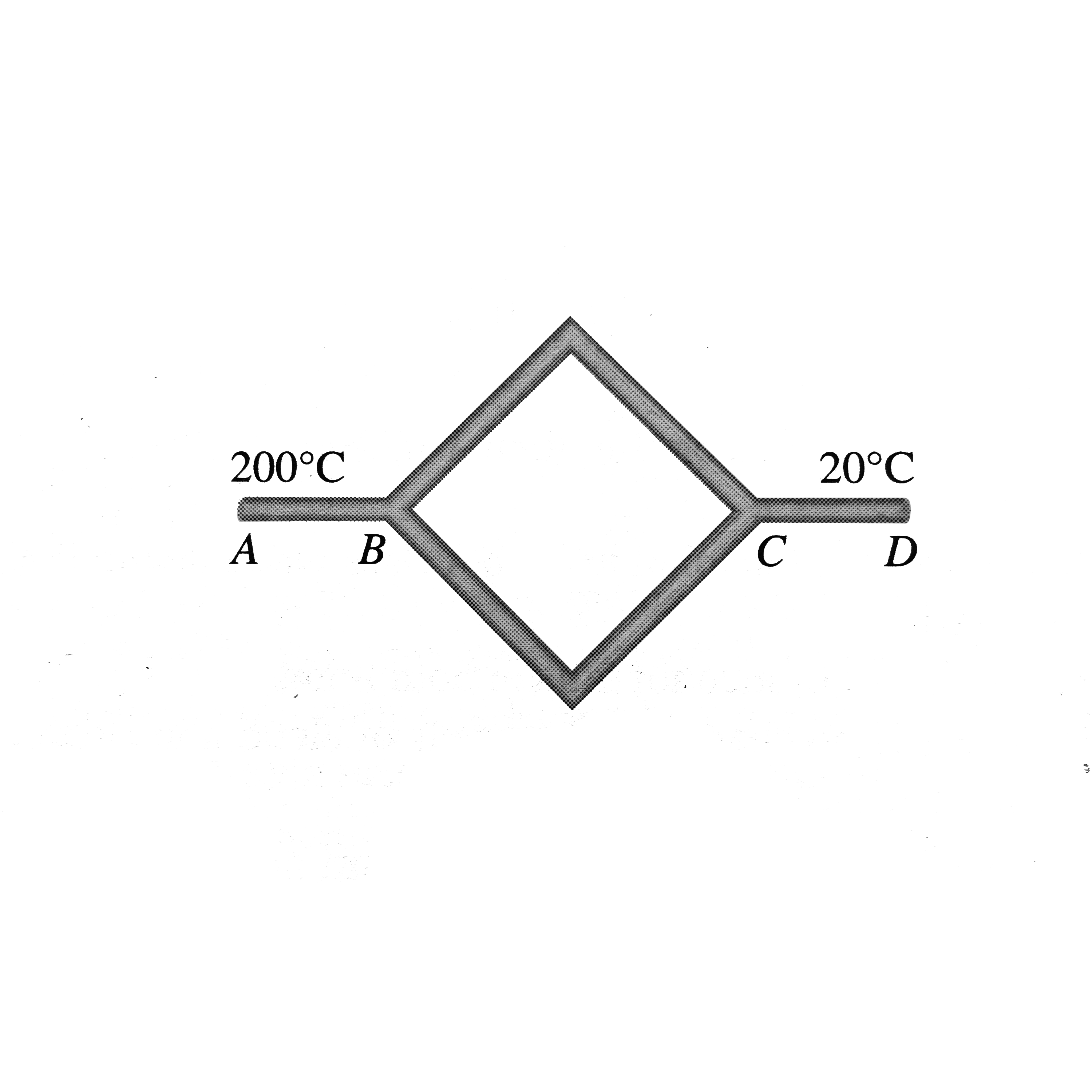
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View Solution
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will be
View SolutionThree isothermal plots (P versus V) A, B and C are plotted at three temperature T1,T2andT3 respectively
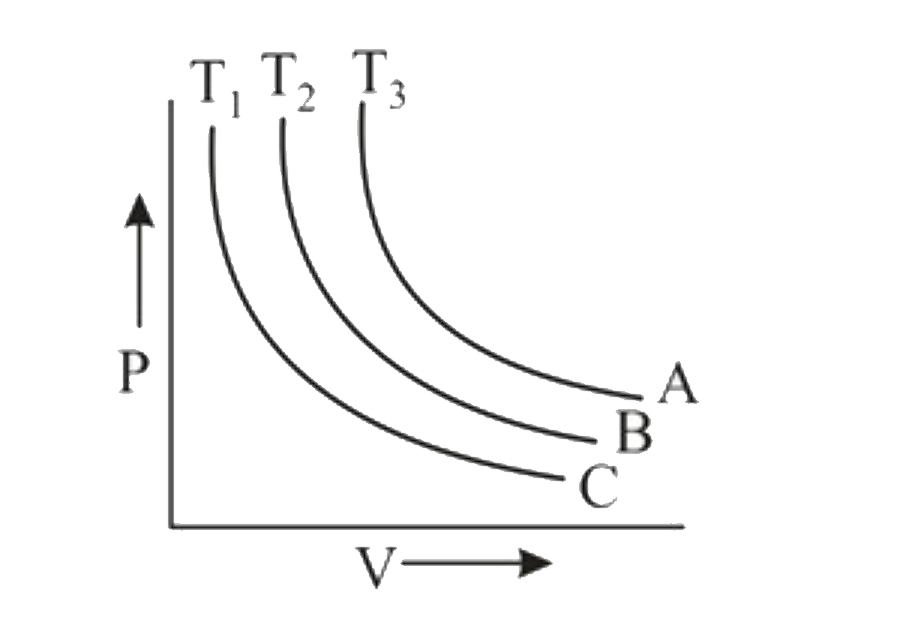
The correct order of the temperature will be
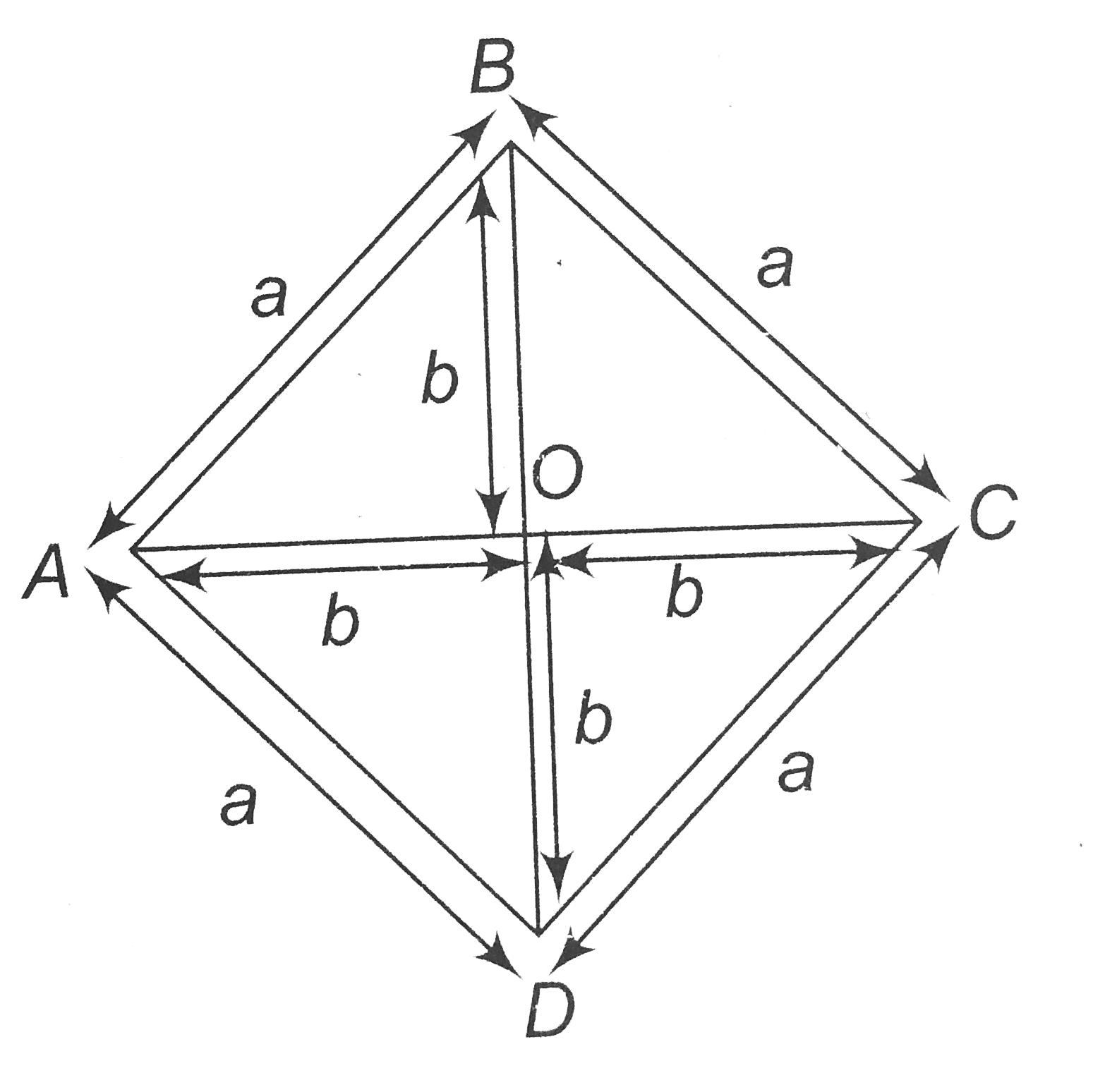
View SolutionAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
View SolutionTwo rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)

View Solution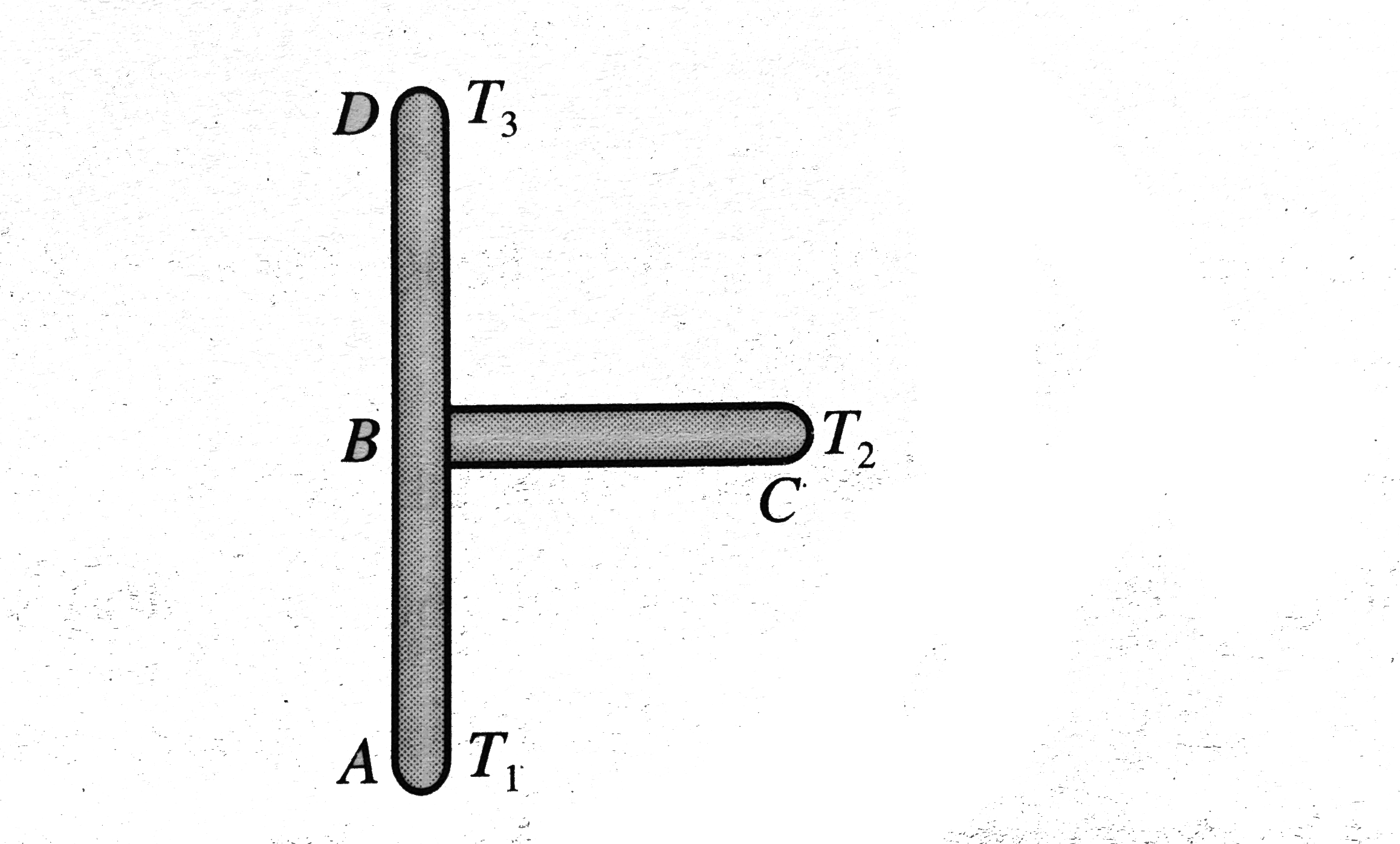
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionFigure illustrates a cycle conducted with n moles of an ideal gas. In the states a and b the gas temperatures are Ta and Tb respectively. Temperature of the gas in the state C is ltbr)
View Solution
