Question

Themperature of a body $\theta$ is slightly more than the temperature of the surrounding ${\theta }_0$ its rate of cooling $\left(R\right)$ versus temperature of body $\left(\theta \right)$ is plotted its shape would be .

Options

A.
B.
C.
D.

Answer

B

Explanation

To solve the problem, we need to analyze the relationship between the rate of cooling (R) and the temperature of the body (θ) when the temperature of the body is slightly more than the temperature of the surroundings (θ₀).

1. Understanding the Concept of Cooling:
- According to Newton's Law of Cooling, the rate of cooling of an object is proportional to the difference in temperature between the object and its surroundings. This can be expressed mathematically as:
\( \frac{d\theta}{dt} = -k(\theta - \theta_0) \)
where \( k \) is a positive constant, \( \theta \) is the temperature of the body, and \( \theta_0 \) is the surrounding temperature.

2. Setting Up the Equation:
- Rearranging the equation, we can express the rate of cooling \( R \) as:
\( R = -\frac{d\theta}{dt} = k(\theta - \theta_0) \)
- Here, \( R \) is positive when \( \theta > \theta_0 \), indicating that the body is cooling down.

3. Analyzing the Temperature Difference:
- Since it is given that \( \theta \) is slightly greater than \( \theta_0 \), we can denote this difference as:
\( \Delta \theta = \theta - \theta_0 \)
- As \( \Delta \theta \) approaches zero, the rate of cooling \( R \) will also be small but positive.

4. Plotting the Graph:
- The relationship \( R = k(\theta - \theta_0) \) indicates that as \( \theta \) increases, \( R \) increases linearly.
- When \( \theta = \theta_0 \), \( R = 0 \). As \( \theta \) increases beyond \( \theta_0 \), \( R \) increases linearly.

5. Conclusion on the Shape of the Graph:
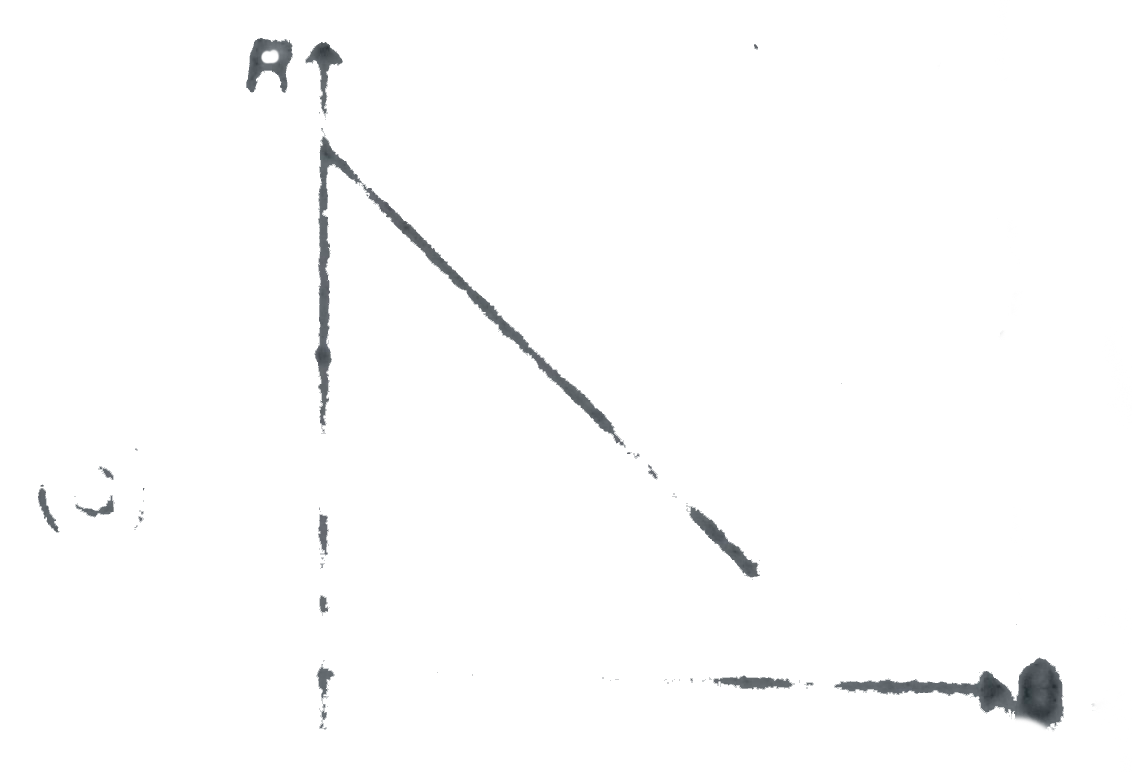
- Therefore, when we plot \( R \) (on the y-axis) against \( \theta \) (on the x-axis), we will get a straight line that starts from the origin (0,0) when \( \theta = \theta_0 \) and rises linearly as \( \theta \) increases.

Final Answer:
The shape of the graph of the rate of cooling \( R \) versus the temperature of the body \( \theta \) is a straight line that passes through the origin and has a positive slope.