The molar heat capacity C for an ideal gas going through a given process is given by C=aT, where 'a' is a constant. If γ=CpCv, the work done by one mole of gas during heating from T0 to ηT0 through the given process will be
a ln(η)
1a ln(η)
a ln(Eta)−(η−1γ−1)RT0
a ln(η)−(γ−1)RT0
The correct Answer is:C
Step by step video & image solution for The molar heat capacity C for an ideal gas going through a given process is given by C=a/T, where 'a' is a constant. If gamma=C_p/C_v, the work done by one mole of gas during heating from T_0 to eta T_0 through the given process will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P=aT−1 where a is a constant .Then the work done by the gas is
Aa. nRTBb. 4nRTCc. 2nRTDd. 6nRT
An ideal gas has an adiabatic exponent γ. In some process its molar heat capacity varies as C=α/T,where α is a constant Find :
(a) the work performed by one mole of the gas during its heating from the temperature T0 to the temperature η times higher ,
(b) the equation of the process in the variables p,V.
View SolutionIf molar heat capacity of the given process (as shown in figure) is C, then

View SolutionTemperature of two moles of an ideal gas is increased by 300K in a process V=aT, where a is positive constant. Find work done by the gas in the given process.
View SolutionThe molar heat capacity of an ideal gas in a process varies as C=CV+αT2 (where CV is mola heat capacity at constant volume and α is a constant). Then the equation of the process is
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
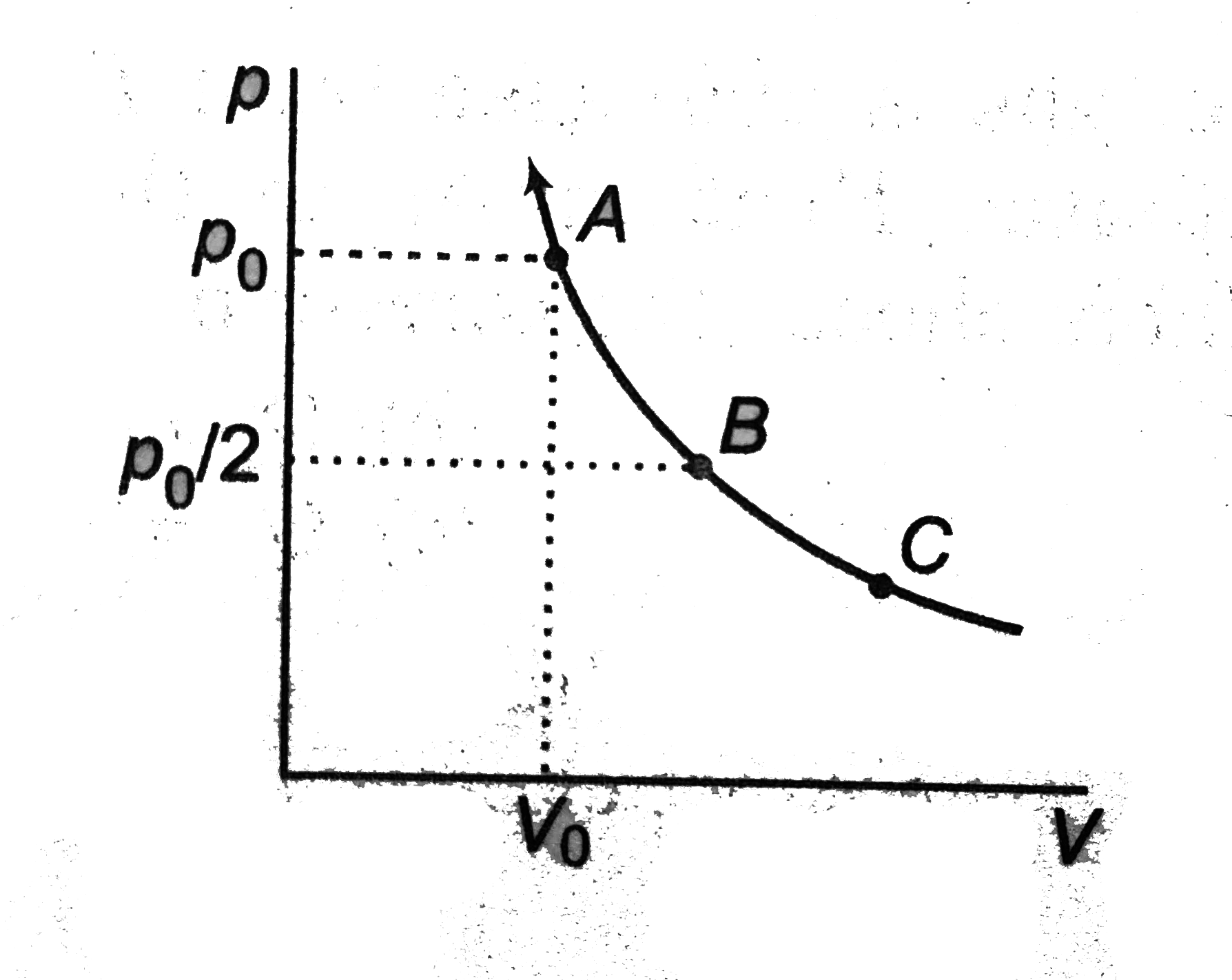
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is

View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View Solution
