A radioactive substance X decys into another radioactive substance Y. Initially, only X was present . λx and λy are the disintegration constant of X and Y. Ny will be maximum when.
NyNx−Ny=λyλx−λy
NxNx−Ny=λxλx−λy
λyNy=λxλx
λyNx=λyλx
The correct Answer is:C
To solve the problem of when the number of substance Y, denoted as Ny, will be maximum, we can follow these steps:
Step 1: Understand the decay process
Initially, we have only substance X present. As time progresses, substance X decays into substance Y. The decay of substance X is characterized by its disintegration constant λx, and the decay of substance Y is characterized by its disintegration constant λy.
Step 2: Write the rate of change of substances
The rate of formation of substance Y (Ny) can be expressed as the difference between the rate at which substance X decays and the rate at which substance Y decays. Mathematically, this can be represented as:
dNydt=λxNx−λyNy
where Nx is the number of nuclei of substance X at time t and Ny is the number of nuclei of substance Y at the same time.
Step 3: Set the condition for maximum Ny
To find the maximum number of substance Y, we need to set the rate of change of Ny to zero:
dNydt=0
This leads to the equation:
λxNx−λyNy=0
Step 4: Rearranging the equation
From the equation above, we can rearrange it to express the relationship between Nx and Ny:
λxNx=λyNy
This implies that the maximum number of substance Y occurs when the decay rate of X equals the decay rate of Y.
Step 5: Express Nx in terms of initial conditions
Initially, when only substance X is present, we can express Nx in terms of the initial number of nuclei Nx0 and the time t:
Nx=Nx0e−λxt
Substituting this back into the equation gives:
λx(Nx0e−λxt)=λyNy
From this, we can solve for Ny:
Ny=λxλyNx0e−λxt
Conclusion
The maximum number of substance Y, Ny, will occur when the decay rates of X and Y are equal, which can be mathematically expressed as:
λxNx=λyNy
Initially, we have only substance X present. As time progresses, substance X decays into substance Y. The decay of substance X is characterized by its disintegration constant λx, and the decay of substance Y is characterized by its disintegration constant λy.
The rate of formation of substance Y (Ny) can be expressed as the difference between the rate at which substance X decays and the rate at which substance Y decays. Mathematically, this can be represented as:
dNydt=λxNx−λyNy
where Nx is the number of nuclei of substance X at time t and Ny is the number of nuclei of substance Y at the same time.
To find the maximum number of substance Y, we need to set the rate of change of Ny to zero:
dNydt=0
This leads to the equation:
λxNx−λyNy=0
From the equation above, we can rearrange it to express the relationship between Nx and Ny:
λxNx=λyNy
This implies that the maximum number of substance Y occurs when the decay rate of X equals the decay rate of Y.
Initially, when only substance X is present, we can express Nx in terms of the initial number of nuclei Nx0 and the time t:
Nx=Nx0e−λxt
Substituting this back into the equation gives:
λx(Nx0e−λxt)=λyNy
From this, we can solve for Ny:
Ny=λxλyNx0e−λxt
The maximum number of substance Y, Ny, will occur when the decay rates of X and Y are equal, which can be mathematically expressed as:
λxNx=λyNy
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive elementX converts into another stable elemnet Y. Half-life of X is 2h. Initally, only X is present. After time t, the ratio of atoms of X and Y is found to be 1:4 Then t in hours is .
View Solution
Knowledge Check
Two samples X and Y contain equal amount of radioactive substances. If 1th16 of the sample Y , remain after 8 hours, then the ratio of half life periods of X and Y is
A2:1B1:2C1:4D4:1
The half-life period of a radioactive element x is same as the mean life time of another radioactive element y. Initially, both of them have the same number of atoms. Then,
(a) x and y have the same decay rate initially
(b) x and y decay at the same rate always
(c) y will decay at a faster rate than x
(d) x will decay at a faster rate than y
View SolutionThe decay constant of a radioactive substance for a and β emission are λa and λβ respectively. It the substance emits a and β simultaneously, the average half life of the material will be_______
View SolutionAt t=0, number of radioactive nuclei of a radioactive substance are x and its radioactivity is y. Half-life of radioactive substance is T. Then,
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The net rate of accumulation of B at any instant is
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
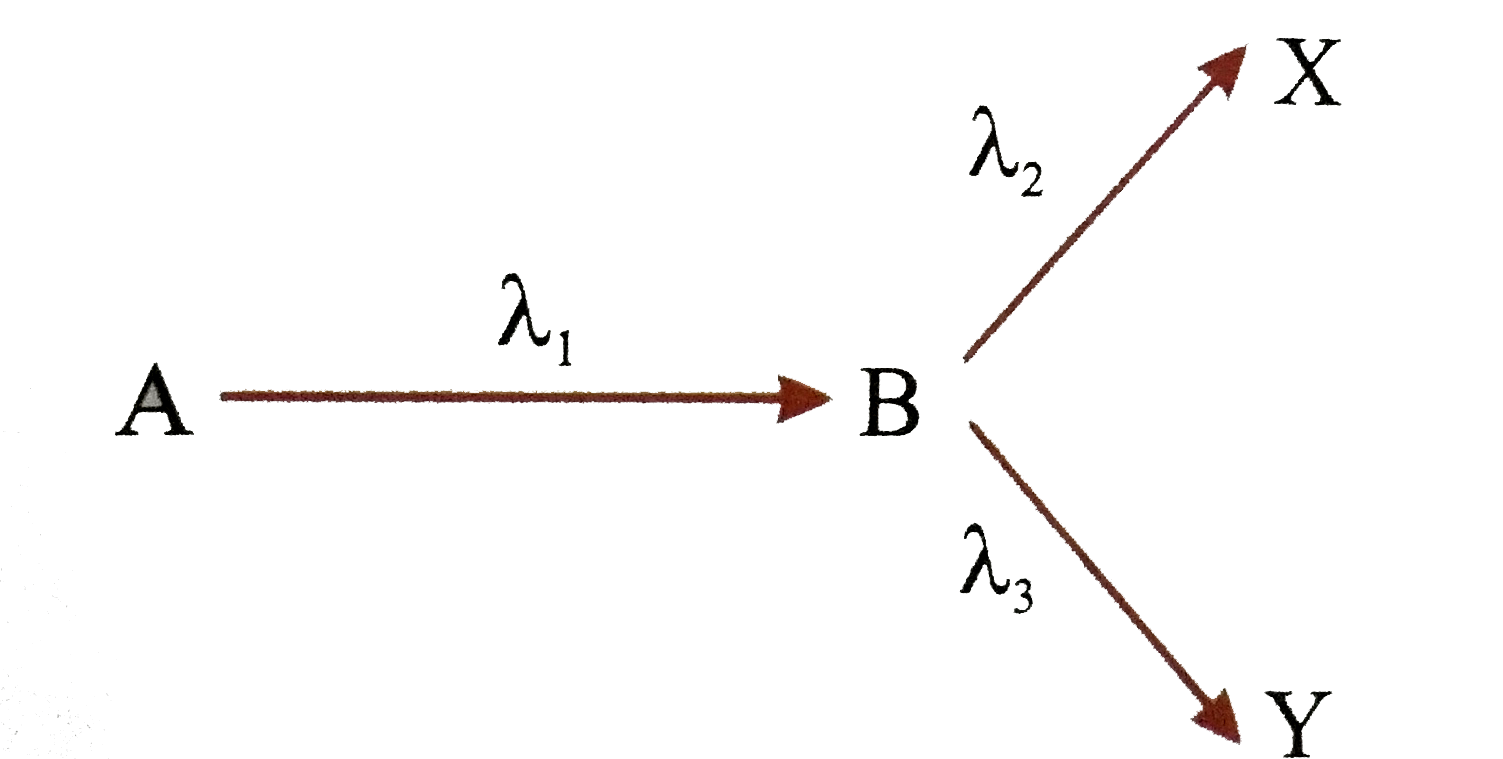
The number of nuclei of B will first increase and then after a maximum value, it decreases for
View SolutionTwo radioactive substances X and Y initially contain equal number of atoms. Their half-lives are 1 hour and 2 hours respectively. Calculate the ratio of their rates of disintegration after four hours.
View SolutionTwo radioactive substance X and Y initially contain equal number of nuclei. X has a half life of 1 hour and Y has a half-life of 2 hours. After 2 hours the ratio of activity of X to that of y is
View Solution
