A radioactive material of half-life T was kept in a nuclear reactor at two different instants. The quantity kept second time was twice of the kept first time. If now their present activities are A1 and A2 respectively, then their age difference equals
Tln2∣∣∣ln.2A1A2∣∣∣
T∣∣∣ln.2A1A2∣∣∣
Tln2∣∣∣ln.A12A2∣∣∣
T∣∣∣ln.A22A1∣∣∣
The correct Answer is:C
To solve the problem step by step, we will analyze the given information about the radioactive material and its activities at two different times.
Step 1: Understand the problem
We have a radioactive material with a half-life T. The first quantity of material is kept at time t1 and the second quantity, which is twice the first, is kept at time t2. We need to find the age difference between the two quantities based on their present activities A1 and A2.
Step 2: Define initial activities
Let:
- The initial activity of the first quantity be A0.
- The initial activity of the second quantity be A′0=2A0 (since it is twice the first).
Step 3: Write the equations for activities
The activity of a radioactive substance at any time t is given by:
A=A0e−λt
where λ is the decay constant.
For the first quantity at time t1:
A1=A0e−λt1
For the second quantity at time t2:
A2=A′0e−λt2=2A0e−λt2
Step 4: Rearranging the equations
From the first equation, we can express A0:
A0=A1e−λt1=A1eλt1
From the second equation:
A′0=A2e−λt2=A22A0e−λt2=A22A1eλt1eλt2
Step 5: Find expressions for t1 and t2
From the equations for A1 and A2:
1. For A1:
A1=A0e−λt1⟹t1=1λln(A0A1)
2. For A2:
A2=2A0e−λt2⟹t2=1λln(2A0A2)
Step 6: Calculate the age difference
The age difference Δt=t1−t2:
Δt=1λ(ln(A0A1)−ln(2A0A2))
Using properties of logarithms:
Δt=1λ(ln(A0A1)−(ln(2)+ln(A0A2)))
This simplifies to:
Δt=1λ(ln(A0A22A1))
Step 7: Substitute λ in terms of half-life
Recall that λ=ln(2)T:
Δt=Tln(2)ln(A22A1)
Final Answer
Thus, the age difference between the two quantities of radioactive material is:
Δt=Tln(2)ln(A22A1)
We have a radioactive material with a half-life T. The first quantity of material is kept at time t1 and the second quantity, which is twice the first, is kept at time t2. We need to find the age difference between the two quantities based on their present activities A1 and A2.
Let:
- The initial activity of the first quantity be A0.
- The initial activity of the second quantity be A′0=2A0 (since it is twice the first).
The activity of a radioactive substance at any time t is given by:
A=A0e−λt
where λ is the decay constant.
A1=A0e−λt1
A2=A′0e−λt2=2A0e−λt2
From the first equation, we can express A0:
A0=A1e−λt1=A1eλt1
A′0=A2e−λt2=A22A0e−λt2=A22A1eλt1eλt2
From the equations for A1 and A2:
1. For A1:
A1=A0e−λt1⟹t1=1λln(A0A1)
A2=2A0e−λt2⟹t2=1λln(2A0A2)
The age difference Δt=t1−t2:
Δt=1λ(ln(A0A1)−ln(2A0A2))
Using properties of logarithms:
Δt=1λ(ln(A0A1)−(ln(2)+ln(A0A2)))
This simplifies to:
Δt=1λ(ln(A0A22A1))
Recall that λ=ln(2)T:
Δt=Tln(2)ln(A22A1)
Thus, the age difference between the two quantities of radioactive material is:
Δt=Tln(2)ln(A22A1)
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
Two radioactive samples of different elements (half-lives t1 and t2 respectively) have same number of nuclei at t=0. The time after which their activities are same is
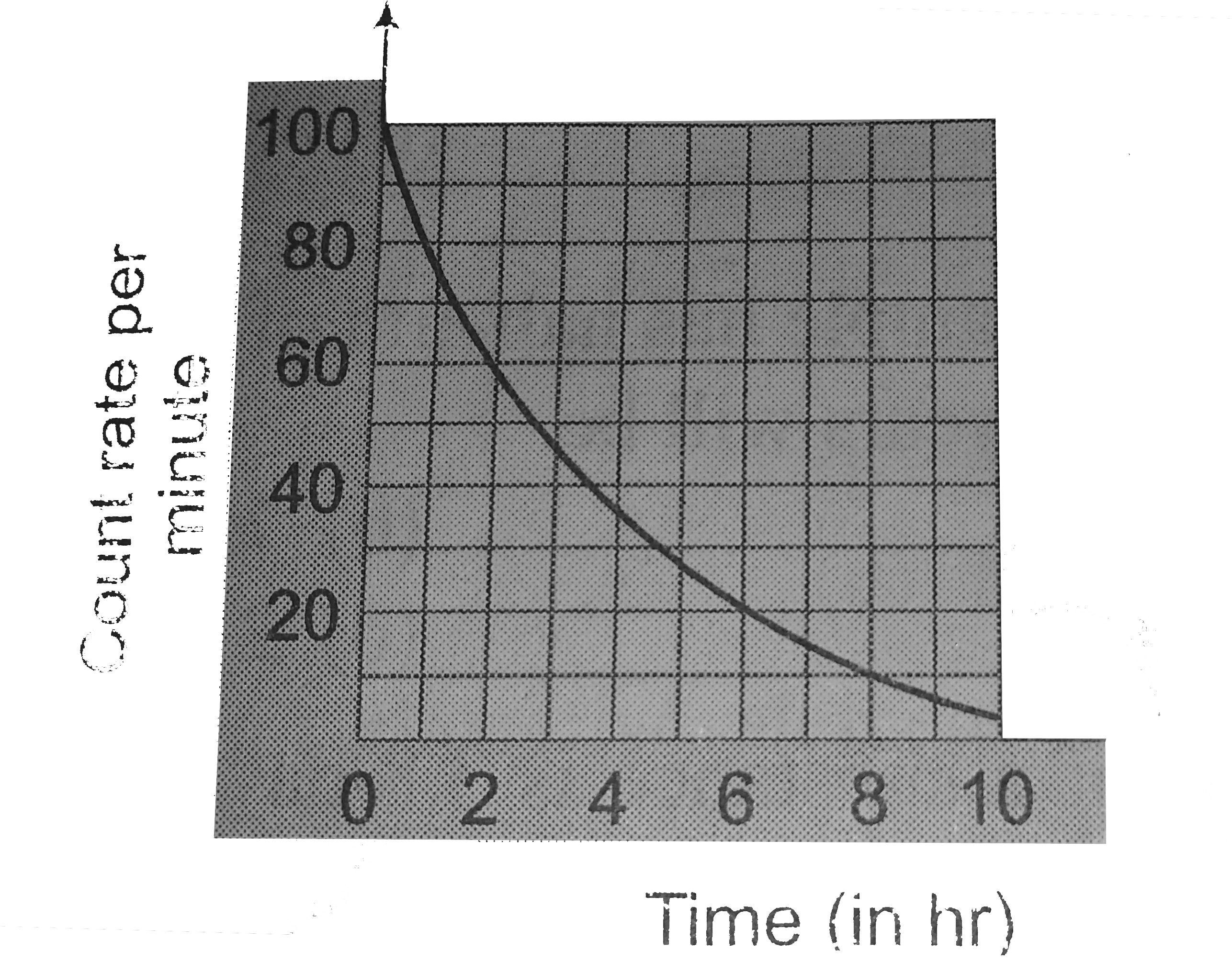
View SolutionThe count rate of 10g of radioactive material was measured at different times and times has been shown in the figure. The half-life of material and the total counts (approximately) in the first half life period, respectively are.
 .
.
View Solution
Knowledge Check
The decay constant of a radioactive isotope is λ. If A1 and A2 are its activites at time t1 and t2 respectively, then the number of nuclei which have decayed the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)
Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View SolutionTwo identical samples (same material and same amout) PandQ of a radioactive substance having mean life T are observed to have activities AP and AQ respectively at the time of observation. If P is older than Q, then the difference in their age is
View SolutionTwo identical samples (same material and same amout) P and Q of a radioactive substance having mean life T are observed to have activities AP and AQ respectively at the time of observation. If P is older than Q, then the difference in their age is
View SolutionA and B participate in a race with acceleration a1anda2 , respectively . A reaches t times earlier than B at finish line and their velocities at finish line are v1andv2 , respectively. If difference between their velocities is v , then find the value of v
View SolutionTwo radioactive substances have half-lives T and 2T. Initially, they have equal number of nuclei. After time t=4T, the ratio of their number of nuclei is x and the ratio of their activity is y. Then,
View SolutionFor a radioactive material, its activity A and rate of change of its activity of R are defined as A=−dNdt and R=−dAdt, where N(t) is the number of nuclei at time t. Two radioactive source P (mean life τ) and Q (mean life 2τ) have the same activity at t=0. Their rates of activities at t=2τ are Rp and RQ, respectively. If RPRQ=ne, then the value of n is:
View SolutionThe half-life of a radioactive sample is T. If the activities of the sample at time t1 and t2 (t1<t2) and R1 and R2 respectively, then the number of atoms disintergrated in time t2−t1 is proportional to
View Solution
