A and B participate in a race with acceleration a1anda2 , respectively . A reaches t times earlier than B at finish line and their velocities at finish line are v1andv2 , respectively. If difference between their velocities is v , then find the value of v
a1+a22t
√a1a2t
a1a2a1+a2t
2a1a2a1+a2t
The correct Answer is:B
To solve the problem step by step, we will use the equations of motion and the relationship between time, acceleration, and velocity.
1. Understanding the Problem:
- A and B are racing with accelerations a1 and a2 respectively.
- A finishes the race t seconds earlier than B.
- The final velocities at the finish line are v1 for A and v2 for B.
- The difference in their final velocities is given as v=v1−v2.
2. Displacement Equation:
- Since both A and B cover the same distance S, we can use the second equation of motion:
S=12at2
- For A:
S=12a1t21
- For B:
S=12a2t22
3. Setting the Displacements Equal:
- Since the distances are equal:
12a1t21=12a2t22
- This simplifies to:
a1t21=a2t22
4. Relating Velocities and Times:
- The final velocity can be expressed as:
v1=a1t1andv2=a2t2
- From the displacement equations, we can express t1 and t2 in terms of S:
t1=√2Sa1andt2=√2Sa2
5. Finding the Ratio of Velocities:
- The ratio of the velocities can be expressed as:
v1v2=a1t1a2t2
- Substituting for t1 and t2:
v1v2=a1√2Sa1a2√2Sa2=a1√a2a2√a1=√a1a2
6. Expressing the Velocity Difference:
- We know from the problem statement that:
v=v1−v2
- Substituting v1 and v2:
v=a1t1−a2t2
- Using the time difference t2−t1=t:
v=a1t1−a2(t1+t)
- Simplifying gives:
v=a1t1−a2t1−a2t=(a1−a2)t1−a2t
7. Final Expression:
- Rearranging gives us the final expression for the difference in velocities:
v=√2a2S⋅t√2S/a1=√2a2a1t
Conclusion:
The value of v is given by:
v=√2a2a1t
- A and B are racing with accelerations a1 and a2 respectively.
- A finishes the race t seconds earlier than B.
- The final velocities at the finish line are v1 for A and v2 for B.
- The difference in their final velocities is given as v=v1−v2.
- Since both A and B cover the same distance S, we can use the second equation of motion:
S=12at2
- For A:
S=12a1t21
- For B:
S=12a2t22
- Since the distances are equal:
12a1t21=12a2t22
- This simplifies to:
a1t21=a2t22
- The final velocity can be expressed as:
v1=a1t1andv2=a2t2
- From the displacement equations, we can express t1 and t2 in terms of S:
t1=√2Sa1andt2=√2Sa2
- The ratio of the velocities can be expressed as:
v1v2=a1t1a2t2
- Substituting for t1 and t2:
v1v2=a1√2Sa1a2√2Sa2=a1√a2a2√a1=√a1a2
- We know from the problem statement that:
v=v1−v2
- Substituting v1 and v2:
v=a1t1−a2t2
- Using the time difference t2−t1=t:
v=a1t1−a2(t1+t)
- Simplifying gives:
v=a1t1−a2t1−a2t=(a1−a2)t1−a2t
- Rearranging gives us the final expression for the difference in velocities:
v=√2a2S⋅t√2S/a1=√2a2a1t
The value of v is given by:
v=√2a2a1t
Similar Questions
Two particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionThe velocities of our molecules are V, 2V, 4V and √2V, respectively. Their r.m.s. speed is
View SolutionTwo particles of mass mA and mB and their velocities are VA and VB respectively collides. After collision they interchanges their velocities, then ratio of mAmB is
View SolutionFind the potential difference Va−Vb between the points (1) and (2) shown in each part of Fig.
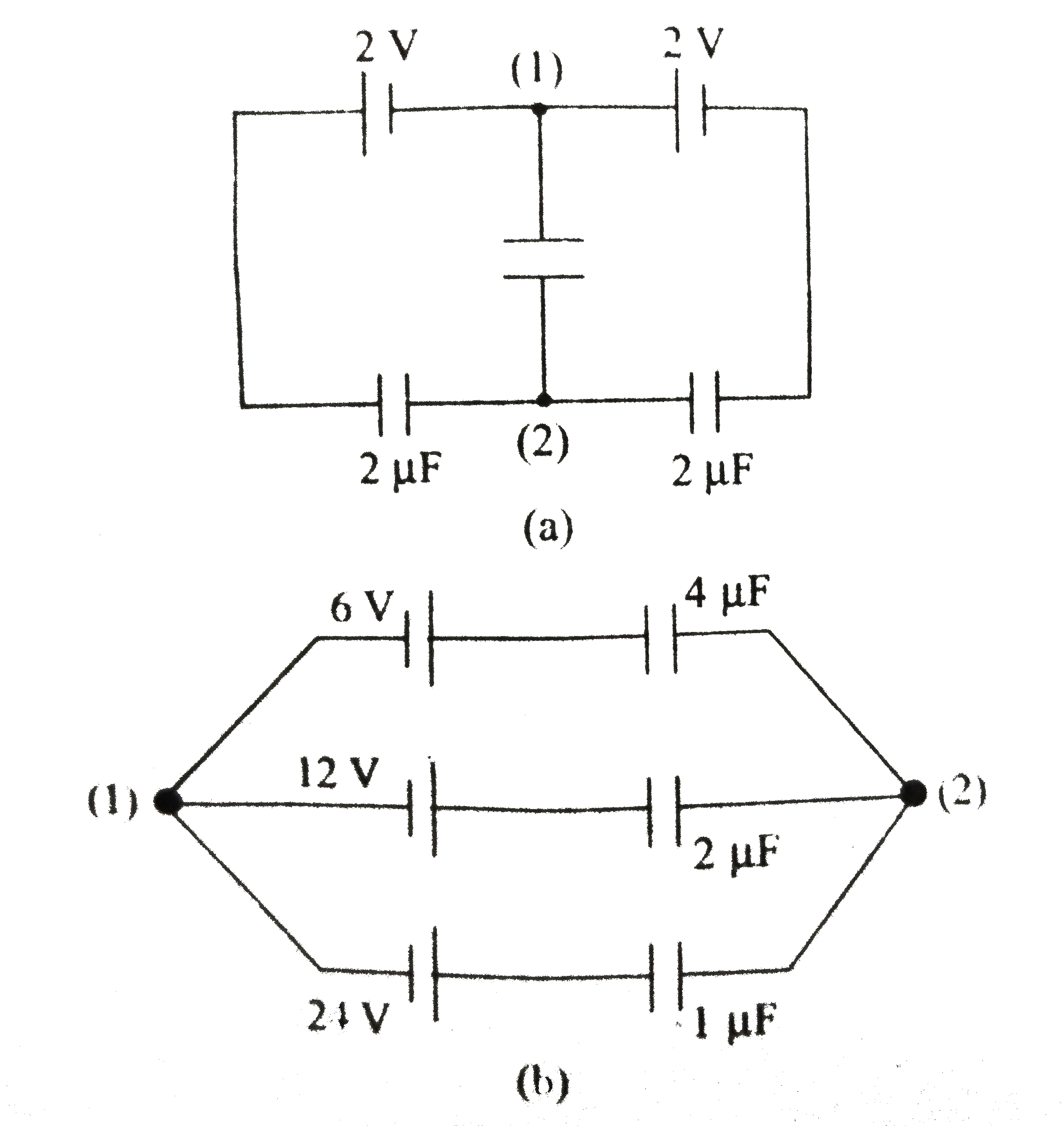 View Solution
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their inertia
View SolutionTwo cars start in a race with velocities u1 and u2 and travel in a straight line with acceleration 'a' and b .If both reach the finish line at the same time,the range of the race is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionTwo bodies A and B of same mass are moving with velocities v and 2v, respectively. Compare their momentum.
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
6. Let vAandvB be the velocities of the particles A and B respectively at the moment A and B meet after start of the motion. If uA=5ms−1anduB=15ms−1, then the magnitude of the difference of velocities vAandvB is
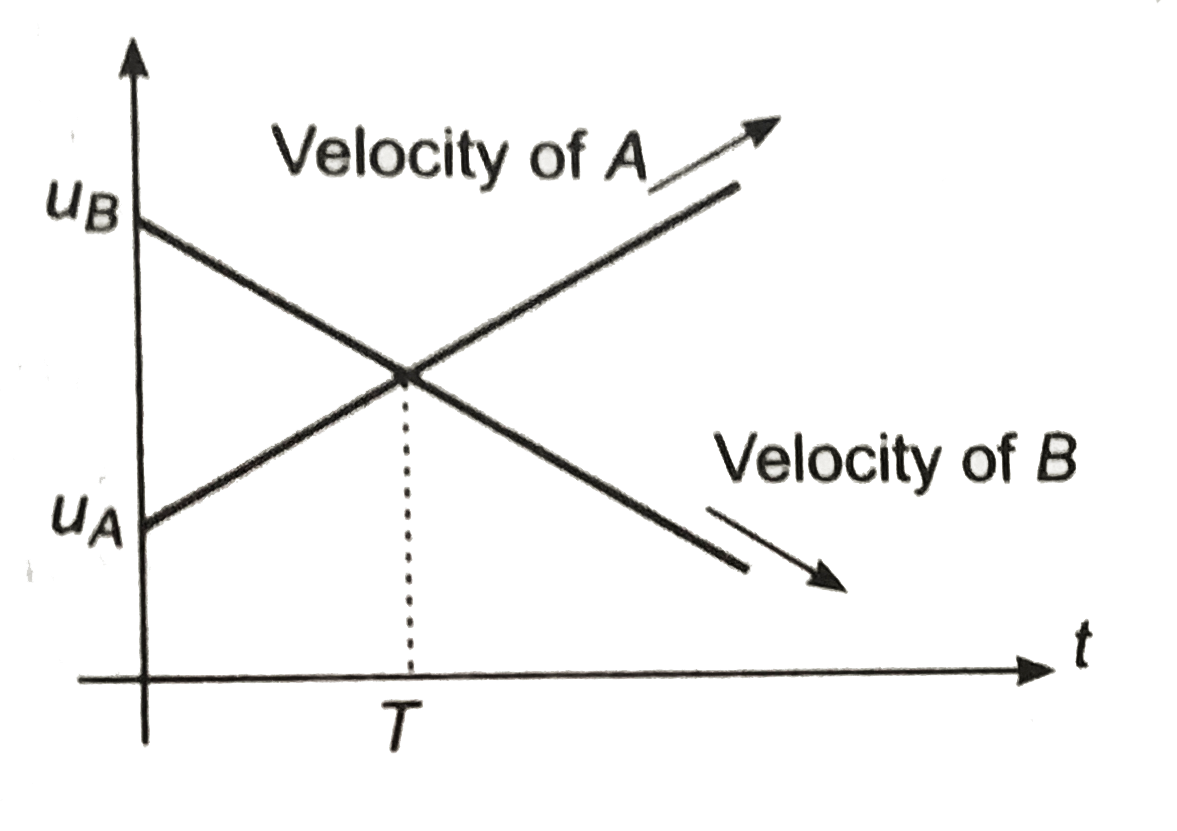 View Solution
View Solution

