An electrons of a stationary hydrogen aton passes form the fifth enegry level to the ground level. The velocity that the atom acquired as a result of photon emission will be
(m is the mass of the electron, R, Rydberg constanrt and h, Planck's constant)
25m24hR
2425hR
24hR25m
25hR24m
The correct Answer is:C
To solve the problem of determining the velocity acquired by a hydrogen atom's electron when it transitions from the fifth energy level to the ground state, we can follow these steps:
Step 1: Identify the Energy Levels
The electron transitions from the fifth energy level (n2 = 5) to the ground state (n1 = 1).
Step 2: Calculate the Wavelength of the Emitted Photon
The wavelength (λ) of the emitted photon can be calculated using the Rydberg formula:
1λ=R⋅(1/n21−1/n22)
Substituting the values:
1λ=R⋅(1/12−1/52)=R⋅(1−125)=R⋅(2425)
Thus, we find:
λ=2524R
Step 3: Calculate the Momentum of the Emitted Photon
The momentum (p) of a photon is given by:
p=hλ
Substituting the expression for λ:
p=h2524R=24hR25
Step 4: Relate Momentum to the Velocity of the Electron
Since the hydrogen atom is stationary before the photon is emitted, the momentum acquired by the electron (which is equal to the momentum of the emitted photon) can be expressed as:
mv=p
Substituting the expression for p:
mv=24hR25
Step 5: Solve for Velocity (v)
To find the velocity (v) of the electron, we rearrange the equation:
v=24hR25m
Final Answer
The velocity that the atom acquired as a result of photon emission is:
v=24hR25m
The electron transitions from the fifth energy level (n2 = 5) to the ground state (n1 = 1).
The wavelength (λ) of the emitted photon can be calculated using the Rydberg formula:
1λ=R⋅(1/n21−1/n22)
Substituting the values:
1λ=R⋅(1/12−1/52)=R⋅(1−125)=R⋅(2425)
Thus, we find:
λ=2524R
The momentum (p) of a photon is given by:
p=hλ
Substituting the expression for λ:
p=h2524R=24hR25
Since the hydrogen atom is stationary before the photon is emitted, the momentum acquired by the electron (which is equal to the momentum of the emitted photon) can be expressed as:
mv=p
Substituting the expression for p:
mv=24hR25
To find the velocity (v) of the electron, we rearrange the equation:
v=24hR25m
The velocity that the atom acquired as a result of photon emission is:
v=24hR25m
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
The recoil energy of a hydrogen atom after it emits a photon in going from n = 5 state to n = 1 state is (M = Mass of H atom, R = Rydberg's constant, h = Planck's constant)
View SolutionHow many spectrual lines are emitted by atomic Hydrogen, when an electron jumps from 5th energy level to ground state ?
View Solution
Knowledge Check
An electron in excited hydrogen atom falls from fifth energy level to second energy level. In which of the following regions, the spectral line will be observed and is part of which series of the atomic spectrum?
AVisible, BalmerBUltraviolet, LymanCInfrared, PaschenDInfrared, BrackettThe diagram shows the energy levels for an electron in a certain atom. Which transition shown represents the emission of photon with the most enegy ?
 AIBIICIIIDIV
AIBIICIIIDIV
An electron in Hydrogen atom ( ground state) jumps to higher energy level x, such that the potential energy of electron becomes half of itstotal energy at ground state. What is the value of x ?
View SolutionSuppose frequency of emitted photon is f0 when the electron of a stationary hydrogen atom jumps from a higher state m to a lower state n. If the atom is moving with a velocity v(<<c) and emits a photon of frequency f during the same transition, then which of the following statement are possible?
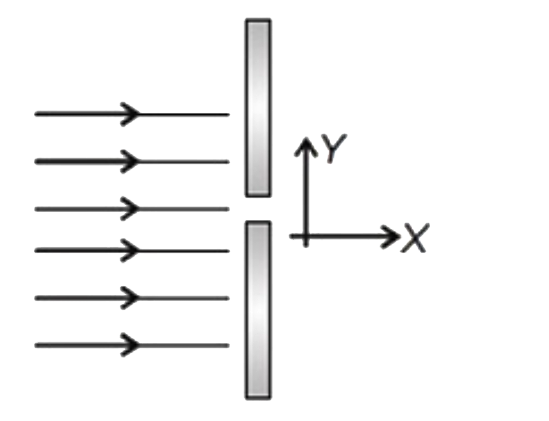
View SolutionA parallel beam of electrons , travelling in x - direction , falls on a slit of width d (see the figure) . If after passing the slit, an electron acquires momentum Py in the y direction, then for a majority of electrons passing through the slit , (h is Planck's constant)
View SolutionIf, an electron in hydrogen atom jumps from an orbit of lelvel n=3 to an orbit of level n=2, emitted radiation has a freqwuency (R= Rydbertg's contant ,c = velocity of light)
View SolutionShows the energy levels for an electron in a certain atom. Which transition shown represented the emission of a photon with the most energy?
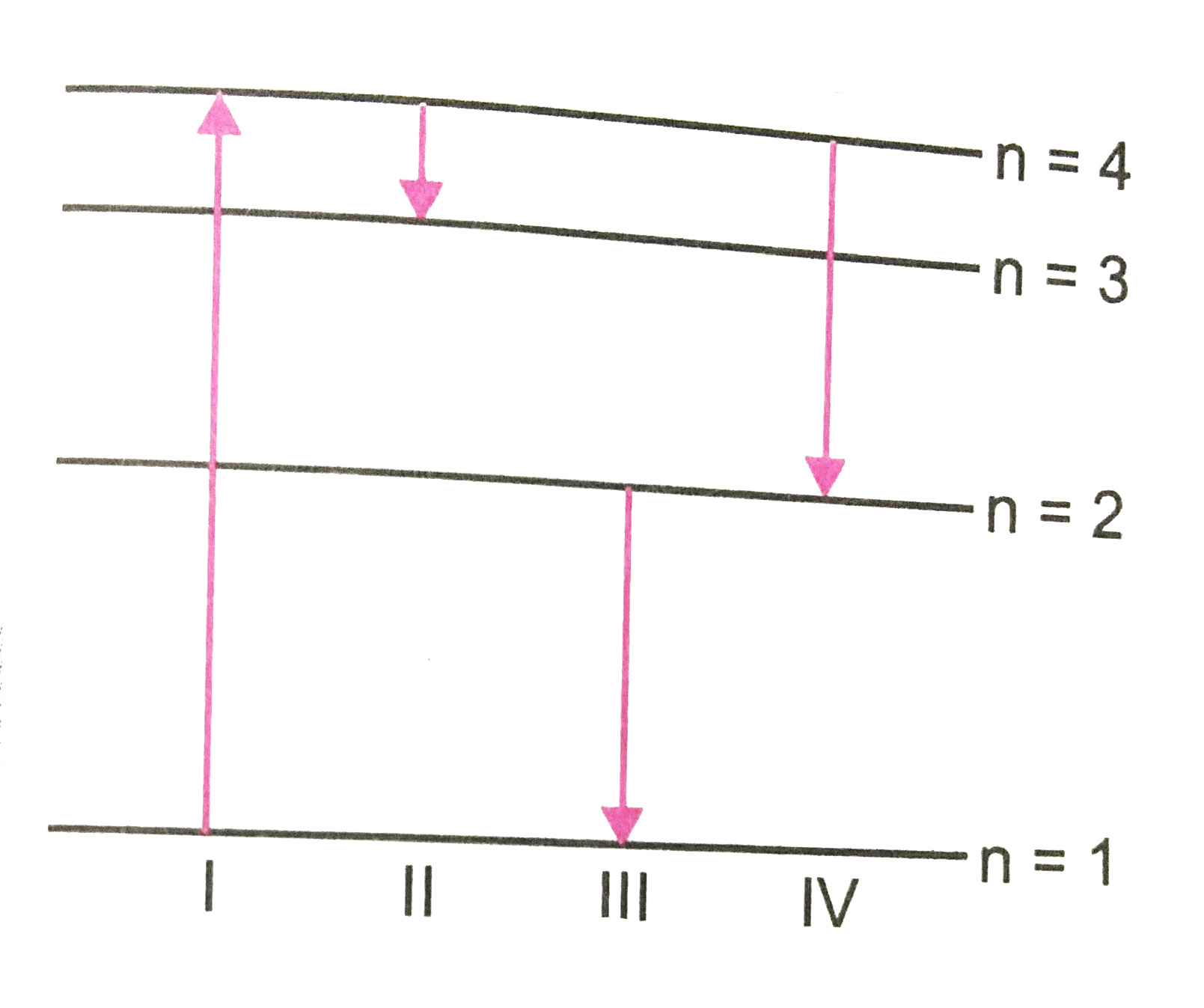
View SolutionThe diagram shows the energy levels for an electron in a certain atom. Which transition shown represents the emission of photon with the most enegy ?

View Solution
