A force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
−2ka2
2ka2
−ka2
ka2
The correct Answer is:C
To find the total work done by the force F=−K(y^i+x^j) on a particle moving from the origin to the point (a,0) and then to (a,a), we can follow these steps:
Step 1: Define the Force
The force acting on the particle is given as:
F=−K(y^i+x^j)
where K is a positive constant.
Step 2: Break the Path into Two Segments
The particle moves in two segments:
1. From the origin (0,0) to (a,0) along the x-axis.
2. From (a,0) to (a,a) along the y-axis.
Step 3: Calculate Work Done in the First Segment
For the first segment, the particle moves along the x-axis where y=0. Thus, the force simplifies to:
F=−K(0^i+x^j)=−Kx^j
The displacement vector dr during this segment is:
dr=dx^i
The work done dW in this segment is:
dW=F⋅dr=(−Kx^j)⋅(dx^i)=0
Since the force is perpendicular to the displacement, the work done in this segment is:
W1=0
Step 4: Calculate Work Done in the Second Segment
For the second segment, the particle moves along the y-axis where x=a. Thus, the force simplifies to:
F=−K(y^i+a^j)=−Ky^i−Ka^j
The displacement vector dr during this segment is:
dr=dy^j
The work done dW in this segment is:
dW=F⋅dr=(−Ka^j)⋅(dy^j)=−Kady
To find the total work done in this segment, we integrate from y=0 to y=a:
W2=∫a0−Kady=−Ka⋅y∣∣∣a0=−Ka2
Step 5: Total Work Done
The total work done W is the sum of the work done in both segments:
W=W1+W2=0−Ka2=−Ka2
Final Answer
Thus, the total work done by the force F on the particle is:
−Ka2
The force acting on the particle is given as:
F=−K(y^i+x^j)
where K is a positive constant.
The particle moves in two segments:
1. From the origin (0,0) to (a,0) along the x-axis.
2. From (a,0) to (a,a) along the y-axis.
For the first segment, the particle moves along the x-axis where y=0. Thus, the force simplifies to:
F=−K(0^i+x^j)=−Kx^j
The displacement vector dr during this segment is:
dr=dx^i
The work done dW in this segment is:
dW=F⋅dr=(−Kx^j)⋅(dx^i)=0
Since the force is perpendicular to the displacement, the work done in this segment is:
W1=0
For the second segment, the particle moves along the y-axis where x=a. Thus, the force simplifies to:
F=−K(y^i+a^j)=−Ky^i−Ka^j
The displacement vector dr during this segment is:
dr=dy^j
The work done dW in this segment is:
dW=F⋅dr=(−Ka^j)⋅(dy^j)=−Kady
To find the total work done in this segment, we integrate from y=0 to y=a:
W2=∫a0−Kady=−Ka⋅y∣∣∣a0=−Ka2
The total work done W is the sum of the work done in both segments:
W=W1+W2=0−Ka2=−Ka2
Thus, the total work done by the force F on the particle is:
−Ka2
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(JIPMER)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
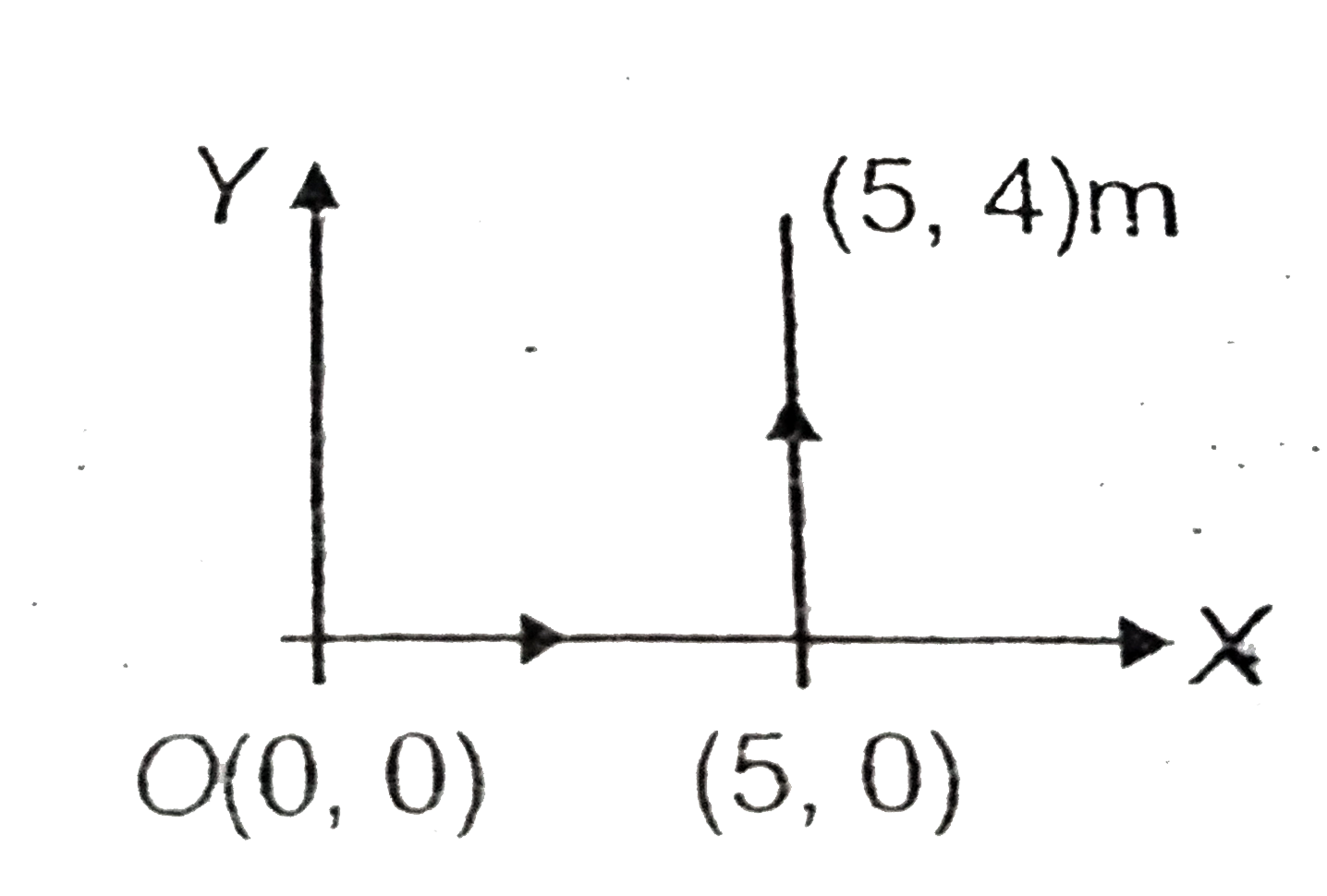
A force →F=(4ˆi+5ˆj)N acts on a particle moving in XY plane. Starting from origin, the particle first goes along x-axis to the point (5.0) m and then parallel to the Y-axis to the point (5,4 m. The total work done by the force on the particle is
View SolutionA particle moves along the x-axis from x=0 to x=5m under the influence of a given by F=7−2x+3x2. The work done by the applied force to the particle is.
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionA moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
View SolutionA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View Solution
