The efficiency of an ideal gas with adiabatic exponent 'γ' for the shown cyclic process would be
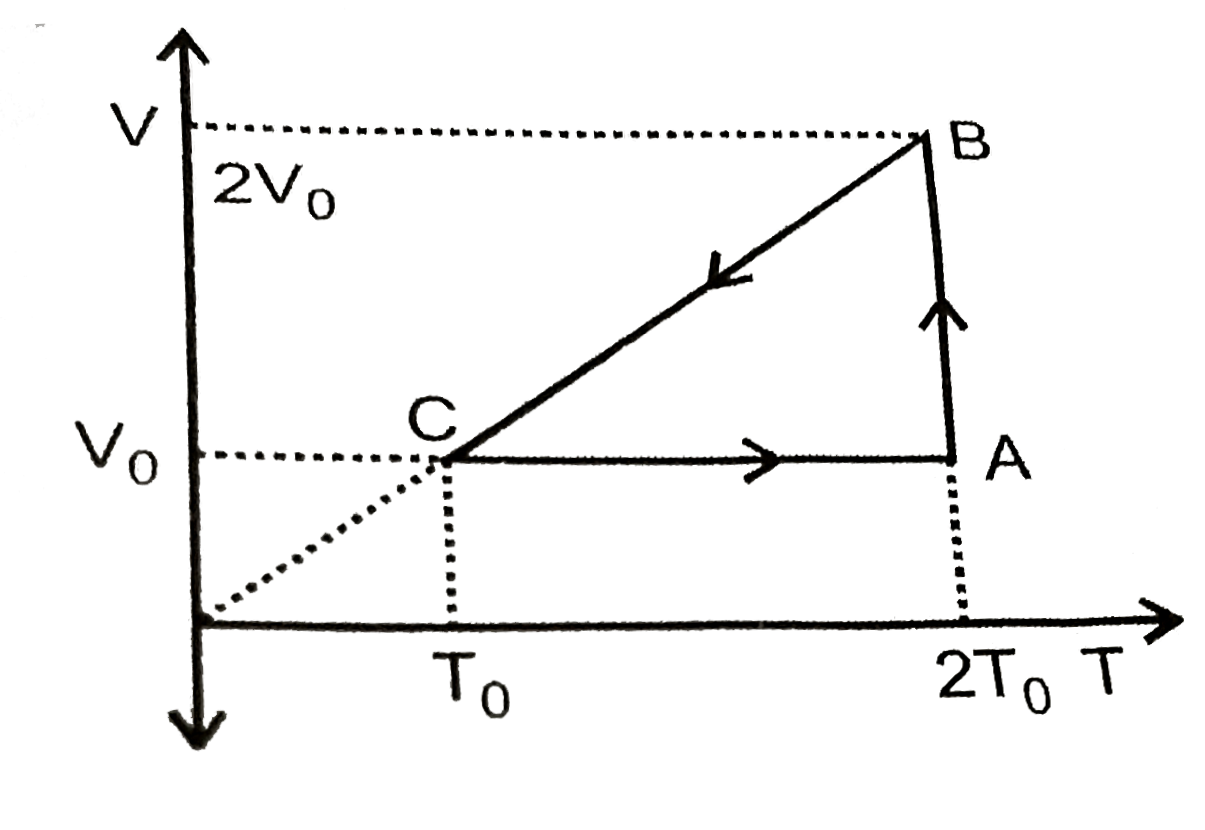
2ln2−1γ/(γ−1)
1−1ln2γ/(γ−1)
2ln2+1γ/(γ−1)
2ln2−1γ/(γ+1)
The correct Answer is:A
Step by step video & image solution for The efficiency of an ideal gas with adiabatic exponent 'gamma' for the shown cyclic process would be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
Find the molar heat capacity of an ideal gas with adiabatic exponent γ for the polytorpic process PVn= Constant.
View SolutionThe volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
View SolutionThe volume of one mode of an ideal gas with adiabatic exponent γ is varied according to the law V=a/T, where a is constant . Find the amount of heat obtained by the gas in this process, if the temperature is increased by ΔT.
View SolutionAdiabatic exponent of a gas is equal to
View SolutionOne mole of an ideal gas whose adiabatic exponent is γ=43 undergoes a process P=200+1V . Then change in internal energy of gas when volume changes from 2m2 to 4m3 is:
View SolutionAn ideal gas with adiabatic exponent γ is heated isochorically. If it absorbs Q amount heat then, fraction of heat absorbed in increasing the internal energy is
View SolutionAn ideal gas is expended adiabatically then
View SolutionAn ideal gas with adiabatic exponent (γ=1.5) undergoes a process in which work done by the gas is same as increase in internal energy of the gas. Here R is gas constant. The molar heat capacity C of gas for the process is:
View SolutionAn ideal gas with adiabatic exponent γ is heated at constant pressure. It absorbs Q amount of heat. Fraction of heat absorbed in increasing the temperature is
View SolutionAn ideal gas with adiabatic exponent γ=43 undergoes a process in which internal energy is related to volume as U=V2 . Then molar heat capacity of the gas for the process is :
View Solution
