Two paper screens A and B are separated by a distance of 100m. A bullet pierces A and B. The hole in B is 10cm below the hole in A. If the bullet is travelling horizontally at the time of hitting the screen A, calculate the velocity of the bullet when it hits the screen A. Neglect resistance of paper and air.
100ms−1
200ms−1
600ms−1
700ms−1
The correct Answer is:D
To solve the problem, we need to determine the velocity of the bullet when it hits screen A. We will use the principles of projectile motion, specifically focusing on the vertical motion of the bullet as it travels between the two screens.
1. Identify the Given Data:
- Distance between screens A and B, d=100m
- Vertical drop from A to B, h=10cm=0.1m
- Acceleration due to gravity, g=10m/s2
2. Determine the Time of Fall:
The bullet falls a vertical distance h while it travels horizontally. We can use the equation of motion for vertical displacement:
h=12gt2
Rearranging this equation to solve for time t:
t2=2hg
t=√2hg=√2×0.110=√0.02=0.1414s
3. Calculate the Horizontal Velocity:
The bullet travels horizontally a distance of d in the same time t:
d=vA⋅t
Rearranging to find the horizontal velocity vA:
vA=dt=1000.1414≈707.1m/s
4. Final Result:
The velocity of the bullet when it hits screen A is approximately 707.1m/s. For practical purposes, we can round this to 700m/s.
Summary:
The velocity of the bullet when it hits screen A is approximately 700m/s.
- Distance between screens A and B, d=100m
- Vertical drop from A to B, h=10cm=0.1m
- Acceleration due to gravity, g=10m/s2
The bullet falls a vertical distance h while it travels horizontally. We can use the equation of motion for vertical displacement:
h=12gt2
Rearranging this equation to solve for time t:
t2=2hg
t=√2hg=√2×0.110=√0.02=0.1414s
The bullet travels horizontally a distance of d in the same time t:
d=vA⋅t
Rearranging to find the horizontal velocity vA:
vA=dt=1000.1414≈707.1m/s
The velocity of the bullet when it hits screen A is approximately 707.1m/s. For practical purposes, we can round this to 700m/s.
The velocity of the bullet when it hits screen A is approximately 700m/s.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrance
12 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - A. Taking it together
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
Two paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: (g=10ms−2)
View SolutionTwo thin wood screens A and B are separated by 200m. A bullet travelling horizontally at a speed of 600ms−1 hits the screen A, penetrates through it and finally emerges out from B making holes in A and B. If the resistance of air and wood arc negligible, the difference of heights of the holes in A and B is
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
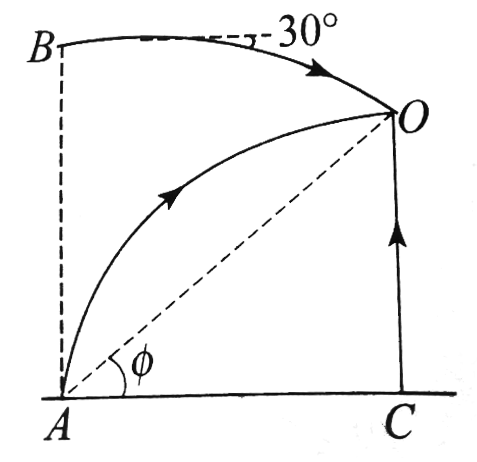
Find the time in which bullets will collide (seconds ):
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.
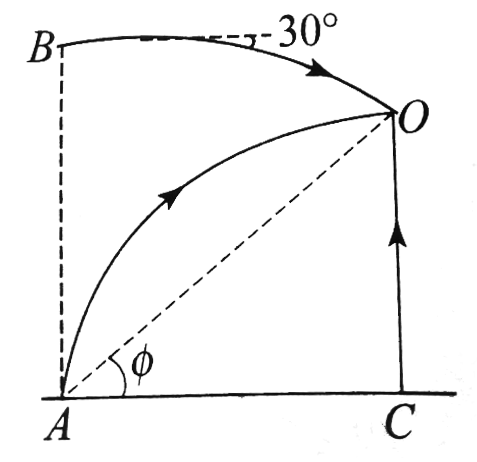
Find the velocity of bullet at A:
View SolutionPoints A and C are on the horizontal ground and A and B are in same vertical plane at a distance of 1500m. Simultaneously bullets are fired from A,Bll and C and they collide at O. The bullets at B is fired at an angle of 30∘with horizontal towards the ground iat velocity 100m/s. the bullet at C is projected vertically upwards at velocity of 100m/s. the bullet projected from A reaches its maximum height at O.

Find the elevation angle ∠θ=∠OAC:
View SolutionA bulley with muzzle velocity 100ms−1 is to be shot at a target 30m away in the same horizontal line. How high above the target must the rifle be aimed so that the bullet will hit the target ?
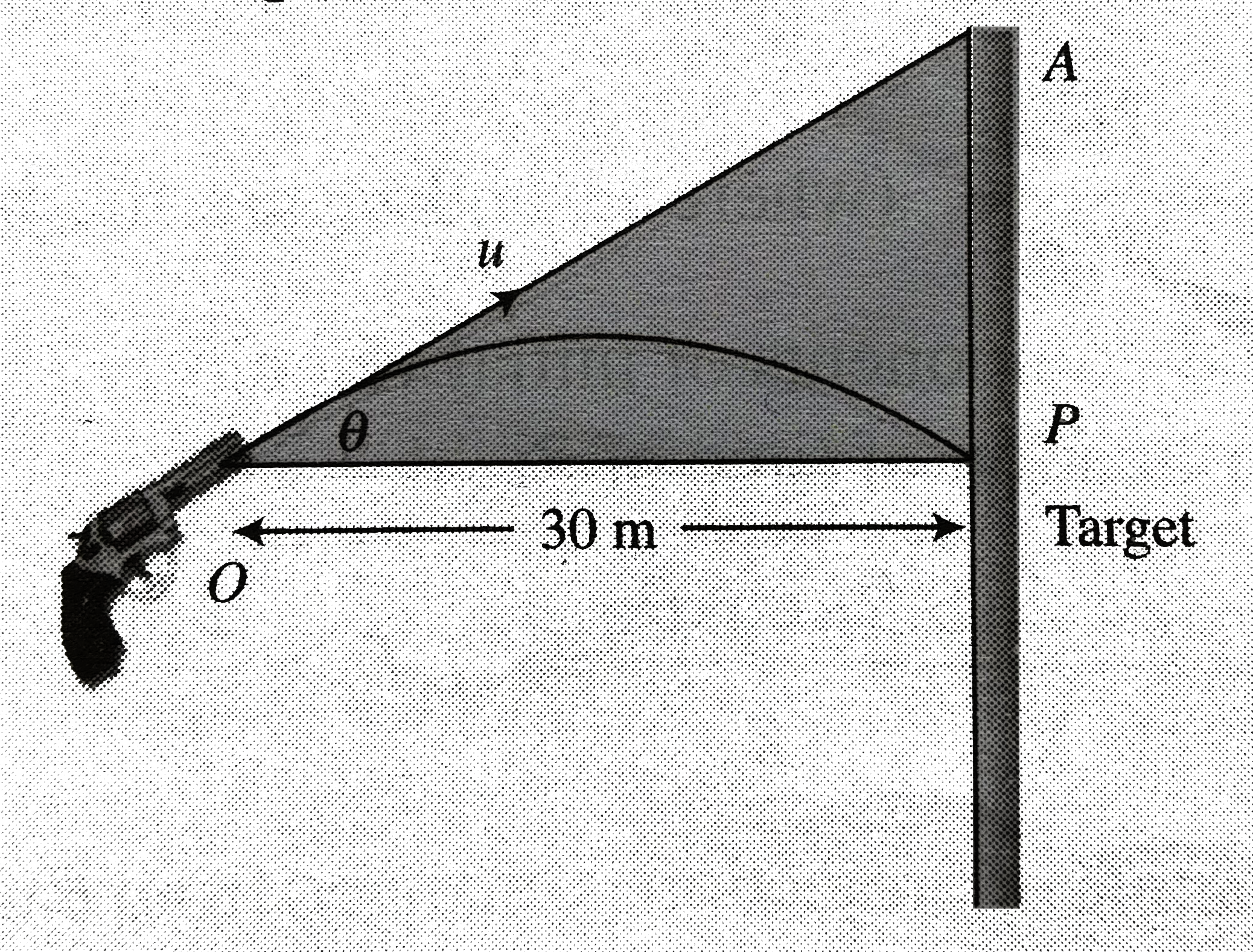 .
.
View SolutionIn the given figure points A and C are on the horizontal ground & A and B are in same vertical plane. Simultaneously bullets are fired from A, B and C and they collide at D. The bullet at B is fired horizontally with speed of 725km/hr and the bullet at C is projected vertically upward at velocity of 545km/hr. Find velocity of the bullet projected from A in m/s.

View Solution(a) A screen is kept at a distance of 1m from the object. A converging lens between the object and the screen, when placed at any of the two positions which are 60cm apart, forms a sharp image of the object on the screen. Find the focal length of the lens.
(b) In the two positions of the lens, lateral size of the image is 4cm and 9cm. Find the size of the object.
View SolutionA 20g bullet pierces through a plate of mass M1=1kg and then comes to rest inside a second plate of mass M2=2.98kg as shown in Fig. It is found that the two plates, initially at rest, now move with equal velocities. Find the percentage loss in the initial velocity of the bullet when it is between M1 and M2. Neglect any loss of material of the plates due to the action of bullet.

View SolutionTwo smooth wedges of equal mass m are placed as shown in figure. All surfaces are smooth. Find the velocities of A & B when A hits the ground.
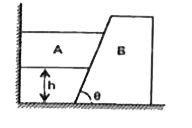
View Solution
