Assertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.
If both Asseration and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:B
To solve the question, we need to analyze both the assertion and the reason provided.
1. Understanding the Scenario:
- Particle-1 is dropped from a tower (initial velocity, u1=0).
- Particle-2 is projected horizontally from the same height (initial vertical velocity, u2=0 in the vertical direction, but has a horizontal component).
2. Time of Flight Calculation:
- Both particles fall from the same height h.
- The time of flight t for both particles can be calculated using the formula for free fall:
h=12gt2
- Rearranging gives:
t=√2hg
- Since both particles are falling from the same height, they will have the same time of flight, t.
3. Final Velocity Calculation:
- For Particle-1 (dropped):
- The final vertical velocity v1 can be calculated using:
v1=u1+gt=0+gt=gt
- For Particle-2 (projected horizontally):
- The final vertical velocity v2 is also given by:
v2=u2+gt=0+gt=gt
- However, Particle-2 also has a horizontal velocity component u0, which does not affect the time of flight but contributes to its overall speed.
4. Conclusion on Speeds:
- The speed of Particle-1 when it hits the ground is v1=gt.
- The speed of Particle-2 when it hits the ground has both vertical and horizontal components. The vertical component is gt and the horizontal component is u0. Thus, its resultant speed can be calculated using Pythagorean theorem:
v2=√(u0)2+(gt)2
- Since u0 is not zero, v2 will be greater than v1.
5. Final Assessment:
- Assertion: Both particles reach the ground simultaneously - True.
- Reason: Both particles strike the ground with different speeds - True.
- However, the reason does not correctly explain the assertion, as the assertion is based on the same height and time of flight, not the difference in speed.
Final Answer:
- The assertion is true, and the reason is also true, but the reason is not the correct explanation of the assertion.
- Particle-1 is dropped from a tower (initial velocity, u1=0).
- Particle-2 is projected horizontally from the same height (initial vertical velocity, u2=0 in the vertical direction, but has a horizontal component).
- Both particles fall from the same height h.
- The time of flight t for both particles can be calculated using the formula for free fall:
h=12gt2
- Rearranging gives:
t=√2hg
- Since both particles are falling from the same height, they will have the same time of flight, t.
- For Particle-1 (dropped):
- The final vertical velocity v1 can be calculated using:
v1=u1+gt=0+gt=gt
- For Particle-2 (projected horizontally):
- The final vertical velocity v2 is also given by:
v2=u2+gt=0+gt=gt
- However, Particle-2 also has a horizontal velocity component u0, which does not affect the time of flight but contributes to its overall speed.
- The speed of Particle-1 when it hits the ground is v1=gt.
- The speed of Particle-2 when it hits the ground has both vertical and horizontal components. The vertical component is gt and the horizontal component is u0. Thus, its resultant speed can be calculated using Pythagorean theorem:
v2=√(u0)2+(gt)2
- Since u0 is not zero, v2 will be greater than v1.
- Assertion: Both particles reach the ground simultaneously - True.
- Reason: Both particles strike the ground with different speeds - True.
- However, the reason does not correctly explain the assertion, as the assertion is based on the same height and time of flight, not the difference in speed.
- The assertion is true, and the reason is also true, but the reason is not the correct explanation of the assertion.
Topper's Solved these Questions
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Match the Columns
4 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - C. Medical entrances gallery
1 Videos
- MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - B. Medical entrance
1 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
- MOTION IN A PLANEBOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
Similar Questions
Assertion : A body droped from a given height and another body projected horizontal from the same height strike the ground simultaneously
Reason : Because horizontal velocity has no effect in the vertical direction .
View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View SolutionA particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)

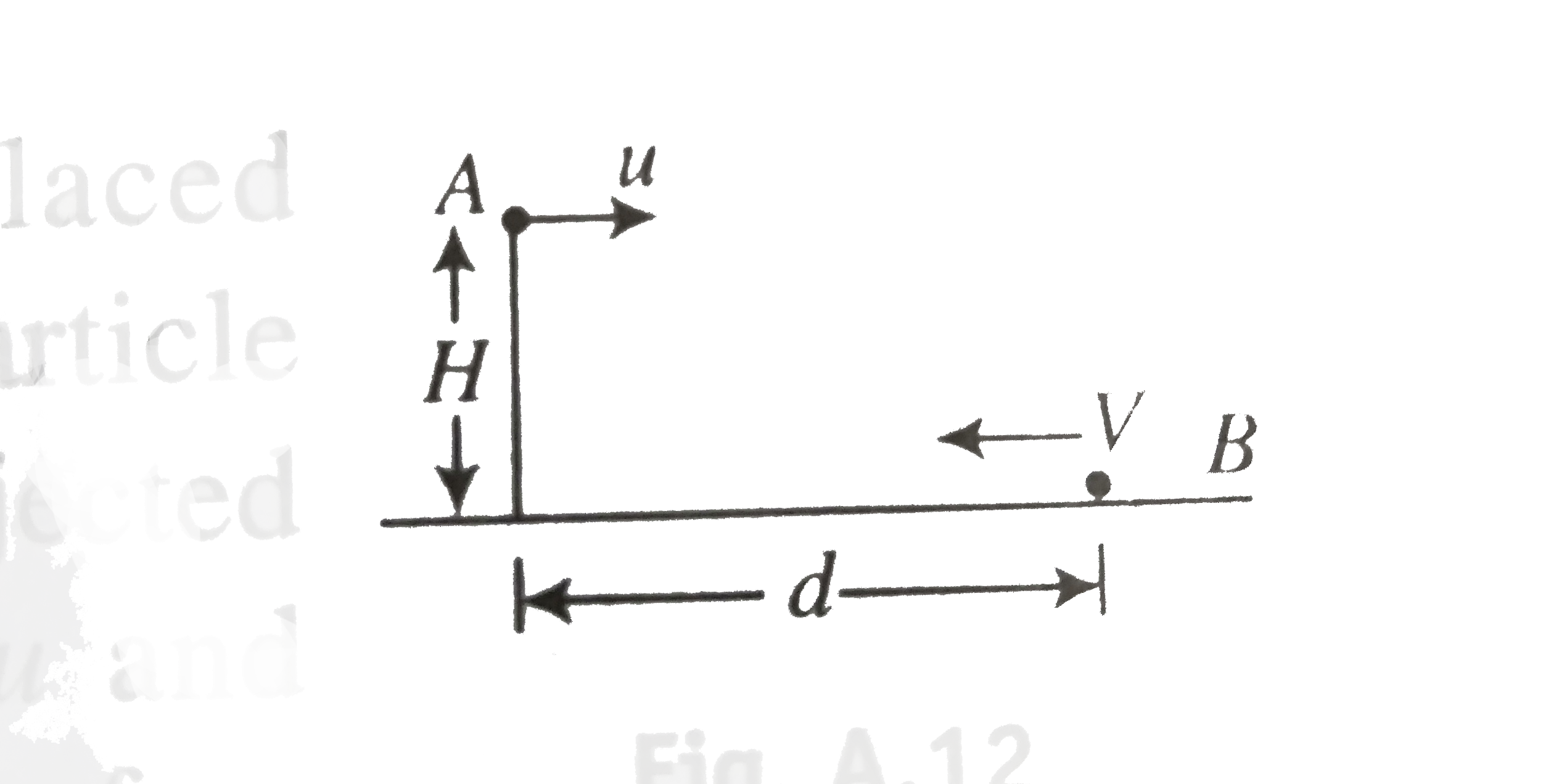
View SolutionTwo particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
View SolutionA particle is dropped from a height h. Another particle which is initially at a horizontal distance d from the first is simultaneously projected with a horizontal velocity u and the two particles just collide on the ground. Then
View SolutionIf a stone and a pencil are dropped simultaneously in vacuum from the top of a tower, which of the two will reach the ground first ? Give reason.
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View SolutionA particle (A) is dropped from a height and another particles (B) is thrown into horizontal direction with speed of 5m/s sec from the same height. The correct statement is
View SolutionA ball is dropped from the top of a tower of height 78.4 m Another ball is thrown down with a certain velocity 2 sec later. If both the balls reach the ground simultaneously, the velocity of the second ball is
View Solution
