A particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

Height of toward is 2u2g
The speed with which particle strikes ground is 2u
Work done by wind force 12μ2
Particle3 strikes the ground after time t=2u/g
The correct Answer is:A, B, D
A particle …………..

in horizontal direction
0=u−g/2t
t=2u/g
in vertical direction
v=u+at
v=0+g.2ug=2u
h=0+12g(2ug)2=2u2g
Topper's Solved these Questions
Similar Questions
A particle Is projected at point 'A' with initial velocity 5m/s at an angle θ=37∘ with the vertical y axis. A strong horizontal wind gives the particle a constant horizontal acceleration 6m/s2 in the x direction. If the particle strikes the ground at a point directly under its released position, determine the height 'h' of point A. The downward acceleration is taken as the constant
g=10m/s2(take sin37∘=35,cos37∘=45)
 View Solution
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
 View Solution
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is ejected from the tube at A with a velocity V at an angle θ with the verticle y-axis at a height h above the ground as shown. A strong horizontal wind gives the particle a constant horizontal acceleration a in the positive x-direction. If the particle strikes the ground at a point directly under its released position and the downward y-acceleration is taken as g then find h.
 View Solution
View SolutionA particle is projected horizontally from the top of a tower with a velocity v0. If v be its velocity at any instant, then the radius of curvature of the path of the particle at that instant is directely proportional to
View SolutionAssertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.View SolutionTwo particles A and B are placed as shown in figure. The particle A, on the top of tower, is projected horizontally with a velocity u and particle B is projected along the surface towards the tower, simultaneously. If both particles meet each other, then the speed of projection of particles B is [ignore any friction]
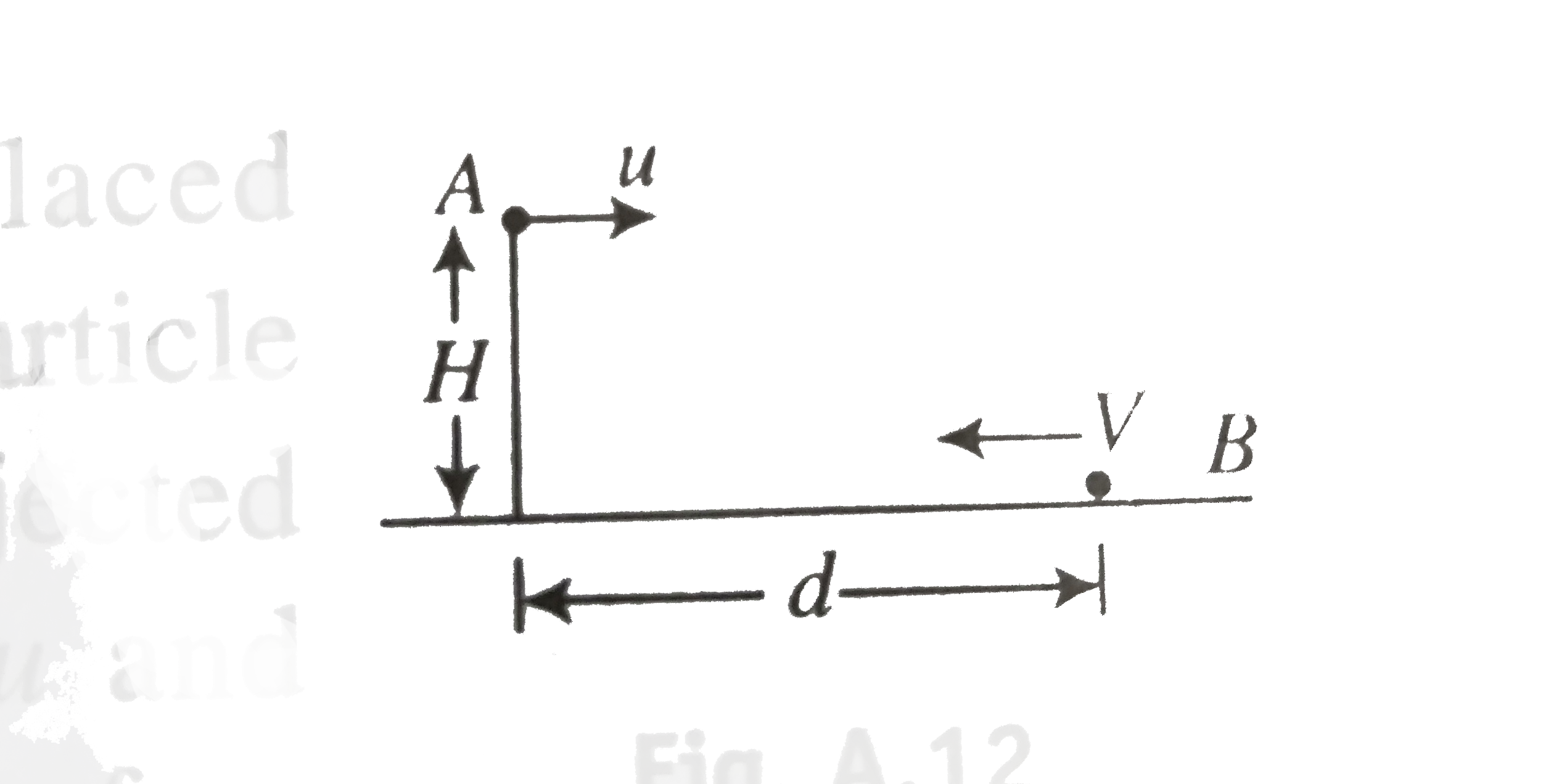 View Solution
View SolutionA particle is projected vertically up from the top of a tower with velocity 10m/s. It reaches the ground in 5s. Find -
(a) Height of tower
(b) Striking velocity of particle at ground
(c ) Distance traversed by particle.
(d) Average speed & average velocity of particle.View Solution

