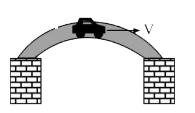
A national roadway bridge over a canal is in the form of an arc of a circle of radius 49 m. What is the maximum speed with which a car can move without leaving the ground at the highest point? (Take,g=9.8ms−2)
19.6ms−1
40ms−1
22ms−1
None of the above
The correct Answer is:C
To solve the problem of determining the maximum speed with which a car can move without leaving the ground at the highest point of a circular arc bridge, we can follow these steps:
1. Understanding the Forces at the Highest Point:
At the highest point of the arc, the car experiences two forces: the gravitational force acting downwards (mg) and the normal force (N) acting upwards. For the car to just stay in contact with the bridge, the normal force must be zero. This means that the gravitational force provides the necessary centripetal force to keep the car moving in a circular path.
2. Setting Up the Equation:
The centripetal force required to keep the car moving in a circular path is given by:
Fc=mv2r
where:
- m is the mass of the car,
- v is the speed of the car,
- r is the radius of the circular arc (49 m).
At the highest point, the only force providing this centripetal force is the weight of the car (mg). Therefore, we can set up the equation:
mg=mv2r
3. Canceling Mass:
Since the mass m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g=v2r
4. Rearranging the Equation:
Rearranging the equation to solve for v2:
v2=rg
5. Substituting Values:
Now, substitute the values for r and g:
- r=49m
- g=9.8m/s2
Thus,
v2=49×9.8
6. Calculating v2:
Calculate v2:
v2=480.2
7. Taking the Square Root:
Finally, take the square root to find v:
v=√480.2≈21.9m/s
8. Conclusion:
Therefore, the maximum speed with which a car can move without leaving the ground at the highest point of the bridge is approximately 22 m/s.
At the highest point of the arc, the car experiences two forces: the gravitational force acting downwards (mg) and the normal force (N) acting upwards. For the car to just stay in contact with the bridge, the normal force must be zero. This means that the gravitational force provides the necessary centripetal force to keep the car moving in a circular path.
The centripetal force required to keep the car moving in a circular path is given by:
Fc=mv2r
where:
- m is the mass of the car,
- v is the speed of the car,
- r is the radius of the circular arc (49 m).
mg=mv2r
Since the mass m appears on both sides of the equation, we can cancel it out (assuming m≠0):
g=v2r
Rearranging the equation to solve for v2:
v2=rg
Now, substitute the values for r and g:
- r=49m
- g=9.8m/s2
v2=49×9.8
Calculate v2:
v2=480.2
Finally, take the square root to find v:
v=√480.2≈21.9m/s
Therefore, the maximum speed with which a car can move without leaving the ground at the highest point of the bridge is approximately 22 m/s.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together
67 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A bridge over a canal is in the form of an arc of a circle of radius 20 m. Calculate the maximum speed at which a motor cycle can pass over the bridge without leaving the ground at the highest point ?.
View SolutionA vehicle is moving on an over bridge which is in the form of a circular arc of radius 10 m. What is the maximum speed with which a vehicle can move through the topmost point on the bridge without losing contact with the bridge ? (g=10m/s2)
View Solution
Knowledge Check
The coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
A√15ms−1B√3ms−1C√30ms−1D√10ms−1
A car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA stone of mass 0.3 kg tied to the end of a string in a horizontal plane in whirled round in a circle of radius 1 m withp. speed of 40 rev/min. What is the tension in the string ? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N ?
View SolutionThe radius of the bump on a road is r. What force does the road exert on a car of mass m when the car passes the highest point on the bump ? Calculate the maximum speed with which the car can pass the highest point before losing contact wtih the road ?
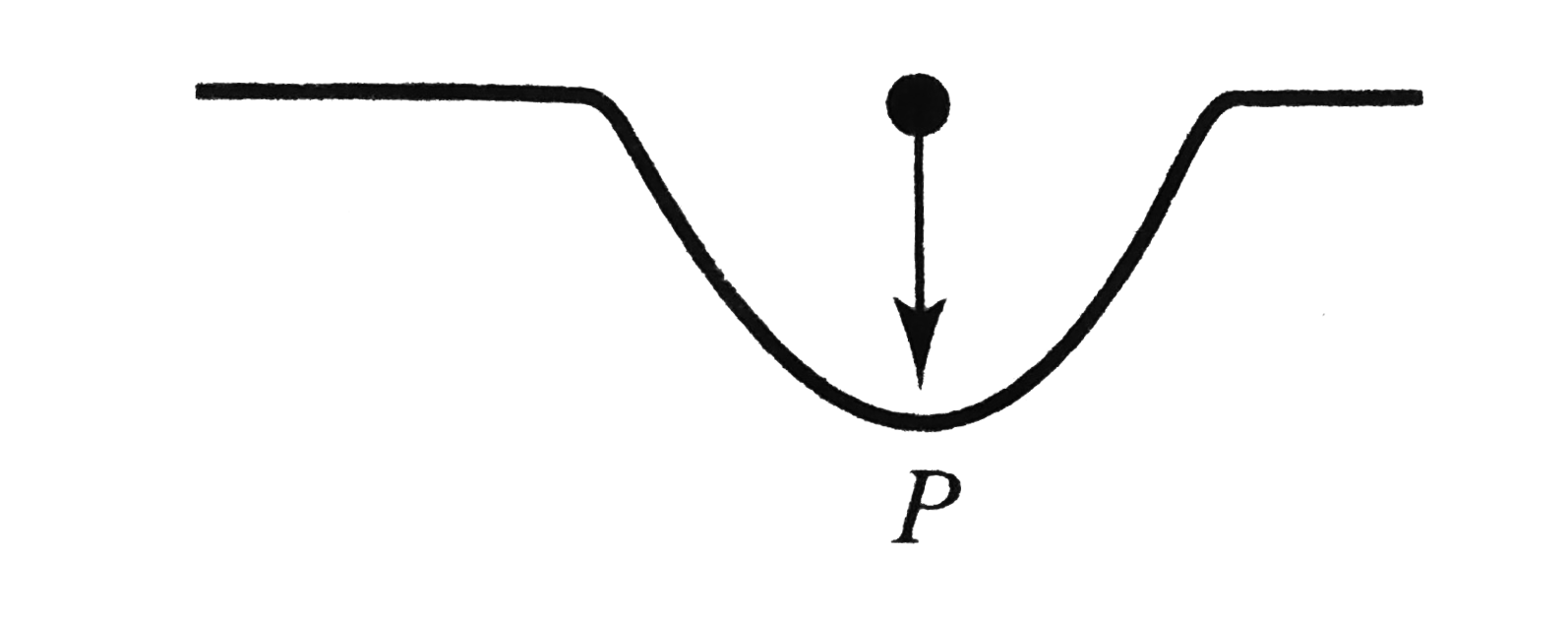
View SolutionA car travelling on a smooth road passes through a curved portion of the road in the form of an arc of circle of radius 10m. If the mass of car is 120kg, find the reaction (in kN) on car at lowest point P where its speed is 20ms−1.
View Solution
