A string of length 0.1 m cannot bear a tension more than 100 N. It is lied to a body of mass 100 g and rotated in a horizontal circle. The maximum angular velocity can be
100rad s−1
1000rad s−1
10000s−1
0.1rad s−1
The correct Answer is:A
To solve the problem, we need to find the maximum angular velocity (ω) at which a body can be rotated in a horizontal circle without exceeding the maximum tension that the string can bear.
1. Identify Given Values:
- Length of the string (radius of the circle, r) = 0.1 m
- Maximum tension (Tmax) = 100 N
- Mass of the body (m) = 100 g = 0.1 kg
2. Understand the Relationship:
- The tension in the string provides the centripetal force required to keep the body moving in a circular path. The formula for centripetal force (Fc) is given by:
Fc=mω2r
- In this case, the maximum tension equals the centripetal force:
Tmax=mω2r
3. Substitute the Known Values:
- Substitute the values of Tmax, m, and r into the equation:
100=0.1⋅ω2⋅0.1
4. Simplify the Equation:
- Rearranging the equation gives:
100=0.01⋅ω2
- To isolate ω2, divide both sides by 0.01:
ω2=1000.01=10000
5. Calculate ω:
- Take the square root of both sides to find ω:
ω=√10000=100 rad/s
Final Answer:
The maximum angular velocity (ω) is 100 rad/s.
---
- Length of the string (radius of the circle, r) = 0.1 m
- Maximum tension (Tmax) = 100 N
- Mass of the body (m) = 100 g = 0.1 kg
- The tension in the string provides the centripetal force required to keep the body moving in a circular path. The formula for centripetal force (Fc) is given by:
Fc=mω2r
- In this case, the maximum tension equals the centripetal force:
Tmax=mω2r
- Substitute the values of Tmax, m, and r into the equation:
100=0.1⋅ω2⋅0.1
- Rearranging the equation gives:
100=0.01⋅ω2
- To isolate ω2, divide both sides by 0.01:
ω2=1000.01=10000
- Take the square root of both sides to find ω:
ω=√10000=100 rad/s
The maximum angular velocity (ω) is 100 rad/s.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together
67 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
One end of a string of length 1 m is tied to a body of mass 0.5 kg. It is whirled in a vertical circle with angular velocity 4 rad s−1. Find the tension in the string when the body is at the lower most point of its motion. (take, g = 10 ms−1)
View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
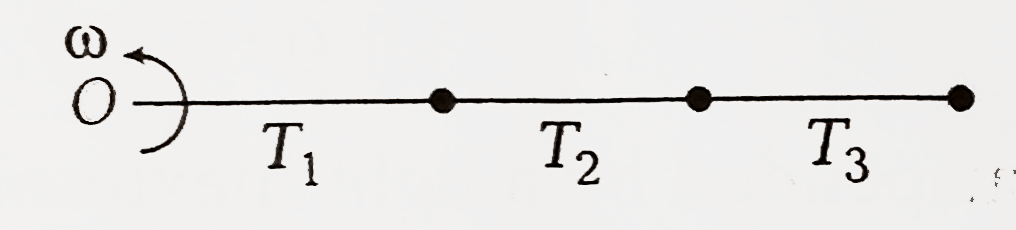
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
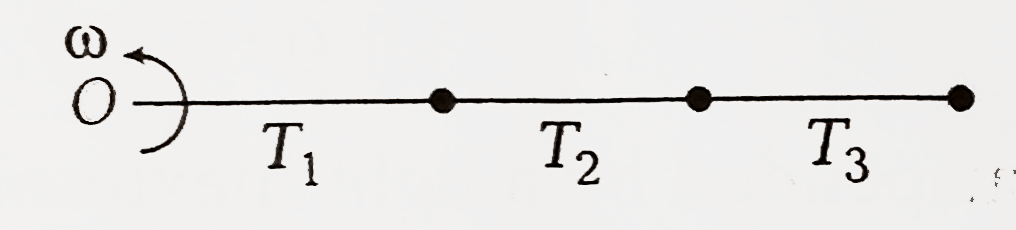
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA body of mass 1 kg is rotated in a horizontal circle of radius 1 m and moves with velocity 2ms−1 The work done in 10 revolutions is
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionThree point masses each of mass'm' are joined together using a string to form an equilateral triangle of side 'a'. The system is placed on a smooth horizontal surface and rotated with a constant angular velocity 'ω' about a vertical axis passing through the centroid. Then the tension in each string is
View SolutionA stone of mass of 16 kg is attached to a string 144 m long and is whirled in a horizontal circle. The maximum tension the string can withstand is 16 Newton . The maximum velocity of revolution that can be given to the stone without breaking it, will be
View SolutionLength of a simple pendulum is 2m and mass of its bob is 0.2 kg. If the tension in the string exceeds 4N, it will break. If the bob is whirled in horizontal plane, the maximum angle the string can make with vertical during rotation is
View Solution
