The radius of the curved road on a national highway is R. The width of the road is b. The outer edge of the road is raised by h with respect to the inner edge so that a car with velocity v can pass safe over it. The value of h is
v2bRg
vRgb
v2Rbg
v2bR
The correct Answer is:A
To solve the problem, we need to determine the height h that the outer edge of the curved road should be raised to ensure that a car can safely navigate the curve at a velocity v.
1. Understanding the Forces: When a car is turning on a curved road, it experiences a centripetal force that keeps it moving in a circular path. This force is provided by the friction between the tires and the road. The road is banked to help provide this force without relying solely on friction.
2. Banking Angle: The banking of the road creates an angle θ with the horizontal. The relationship between the angle of banking, the velocity of the car, the radius of the curve, and the acceleration due to gravity is given by the equation:
tan(θ)=v2gR
where g is the acceleration due to gravity.
3. Relating Height and Width: The height h of the outer edge of the road can be related to the width b of the road and the angle θ using the tangent function:
tan(θ)=hb
4. Equating the Two Expressions for tan(θ): Since both expressions represent tan(θ), we can set them equal to each other:
hb=v2gR
5. Solving for Height h: Rearranging the equation to solve for h:
h=b⋅v2gR
6. Final Expression: Thus, the height h that the outer edge of the road should be raised is given by:
h=bv2gR
Conclusion:
The value of h is bv2gR.
tan(θ)=v2gR
where g is the acceleration due to gravity.
tan(θ)=hb
hb=v2gR
h=b⋅v2gR
h=bv2gR
The value of h is bv2gR.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Taking it together
67 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A road is 10 m wide. Its radius of curvature is 50 m . The outer edge is above the lower edge by a distance of 1.5 m . This road is most suited for the velocity
View SolutionA road is 8 m wide. Its radius of curvature is 40 m. The outer edge is above the lower edge by a distance of 1.2 m. This road is most suited for a velocity of
View SolutionThe radius of the bump on a road is r. What force does the road exert on a car of mass m when the car passes the highest point on the bump ? Calculate the maximum speed with which the car can pass the highest point before losing contact wtih the road ?
View SolutionA car moves at a constant speed on a straigh but hilly road. One section has a crest and dip of the 250m radius.
(a) As the car passes over the crest the normal force on the car is half the 16kN weight of the car. What will the noraml force on the car its passes through th ebottom of the dip?
(b) What is the greatest speed at which the car can move without leaving the road at the top of the hill ?
(c) Moving at a speed found in part (b) what will be the normal force on the car as it moves through the bottom of the dip? (Take, g=10m/s2)
View SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate
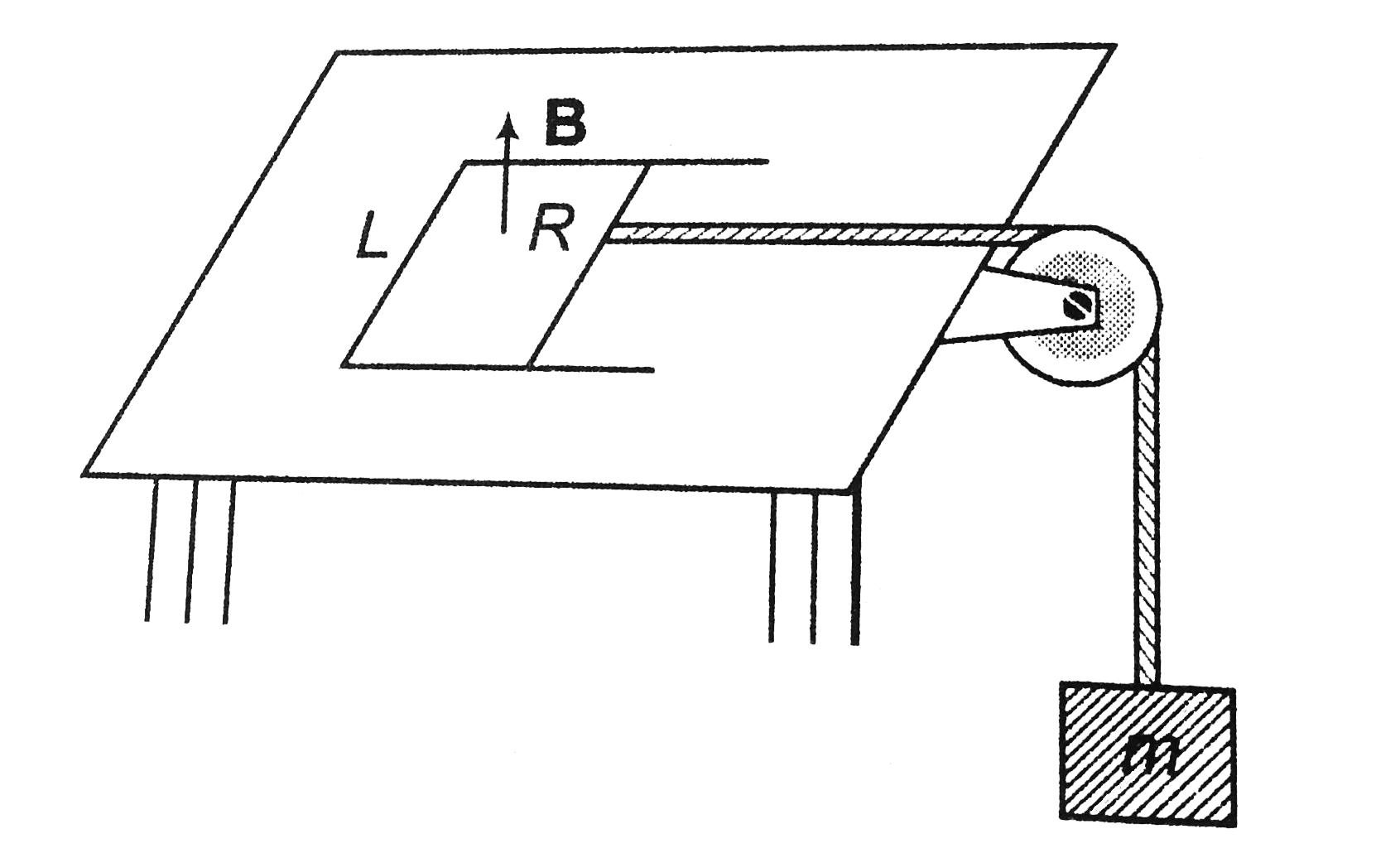
a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.
View SolutionA car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficeint of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
View SolutionA train has to negotiate a curve of radius 2000 m. By how much should the outer rail be raised with respect to inner rail for a speed of 72kmh−1. The distance between the rails is 1 m.
View SolutionA unifrom magnetic field B existis in the space between two coaxial cylinders of radius 'a' and 'b' respectivelly. The direction of magnetic field is parallel to the axis of the cylinder a shown in figure . A negatively charged particle of change -q and mass m is projected from teh outer surface of inner cyclinder with an initial velocity v0 in the radialy outward direction . The minimum value to of magnetic field so that the particle does not hit the surface of the outer cyclinder is

View SolutionA block of mass m height 2h and width 2b rests on a flat car which moves horizontally with constant acceleration a as shown in figure. Determine

a. the value of the acceleration at which slipping of the block on the car starts, if the coefficient of friction is μ.
b. the value of the acceleration at which block topples about A, assuming sufficient friction to prevet slipping and
c. the shortest distance in which it can be stopped from a speed of 20ms−1 with constant deceleration so that the block is not disturbed. The following data are given b=0.6m,h=0.9m,μ=0.5 and g=10ms−2
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends on the properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
Which object would first acquire half of their respective terminal speed in minimum time from start of the motion of all were released simultaneously ?
View Solution