Two concentric metallic spherical shells are given positive charges . Then
the outer sphere is always at a higher potential
the inner sphere is always at a higher potential
Both the spheres are at the same potential
no prediction can be made about their potentials unless the actual value of charges and radii are known
To solve the problem regarding the potential of two concentric metallic spherical shells with positive charges, we will follow these steps:
Step 1: Understand the Configuration
We have two concentric metallic spherical shells. Let:
- The inner shell have radius R1 and charge Q1.
- The outer shell have radius R2 and charge Q2.
Step 2: Determine the Electric Potential
The electric potential V at a distance r from a charged spherical shell is given by:
- For a point outside the shell (at r>R):
V=14πϵ0Qr
- For a point inside the shell (at r<R):
V=14πϵ0QR
Step 3: Calculate the Potential at the Inner Shell
The potential Vinner at the inner shell (radius R1) due to both shells is:
Vinner=VQ1+VQ2
Where:
- VQ1=14πϵ0Q1R1 (potential due to the inner shell)
- VQ2=14πϵ0Q2R2 (potential due to the outer shell)
Thus,
Vinner=14πϵ0Q1R1+14πϵ0Q2R2
Step 4: Calculate the Potential at the Outer Shell
The potential Vouter at the outer shell (radius R2) is:
Vouter=VQ2+VQ1
Where:
- VQ2=14πϵ0Q2R2 (potential due to the outer shell)
- VQ1=14πϵ0Q1R2 (potential due to the inner shell, valid since we are at R2)
Thus,
Vouter=14πϵ0Q2R2+14πϵ0Q1R2
Step 5: Compare the Potentials
Now we compare Vinner and Vouter:
- Vinner has the term Q1R1 which is greater than Q1R2 since R1<R2.
- Therefore, Vinner>Vouter.
Conclusion
The inner shell is always at a higher potential than the outer shell when both are given positive charges.
We have two concentric metallic spherical shells. Let:
- The inner shell have radius R1 and charge Q1.
- The outer shell have radius R2 and charge Q2.
The electric potential V at a distance r from a charged spherical shell is given by:
- For a point outside the shell (at r>R):
V=14πϵ0Qr
- For a point inside the shell (at r<R):
V=14πϵ0QR
The potential Vinner at the inner shell (radius R1) due to both shells is:
Vinner=VQ1+VQ2
Where:
- VQ1=14πϵ0Q1R1 (potential due to the inner shell)
- VQ2=14πϵ0Q2R2 (potential due to the outer shell)
Vinner=14πϵ0Q1R1+14πϵ0Q2R2
The potential Vouter at the outer shell (radius R2) is:
Vouter=VQ2+VQ1
Where:
- VQ2=14πϵ0Q2R2 (potential due to the outer shell)
- VQ1=14πϵ0Q1R2 (potential due to the inner shell, valid since we are at R2)
Vouter=14πϵ0Q2R2+14πϵ0Q1R2
Now we compare Vinner and Vouter:
- Vinner has the term Q1R1 which is greater than Q1R2 since R1<R2.
- Therefore, Vinner>Vouter.
The inner shell is always at a higher potential than the outer shell when both are given positive charges.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
There are two concentric spherical shells with inner shell having positive charge q and outer shell having a charge -q. Now outer shell is supplied a charge -2q and inner shell is earthed, Calculate the ratio of initial and final capacities of the system. (If a = 3R, b= 5R)
View SolutionThree concentric metallic spherical shells of radii R, 2R, 3R are given charges Q1Q2Q3, respectively. It is found that the surface charge densities on the outer surface of the shells are equal. Then, the ratio of the charges given to the shells Q1:Q2:Q3 is
View SolutionFigure shows three concentric metallic spherical shells. The outermost shell has charge q2, the inner most shell has charge q1, and the middle shell is uncharged. The charge appearing on the inner surface of outermost shell is
View SolutionA metallic spherical shell of radius r1 is surrounded by another concentric metallic spherical shell of radius r2. The space between the two shells is filled with a dielectric of dielectric constant K. If a charge Q is given to the inner shell, the charge appearing on the outer surface of the outer shell is
View SolutionA and B are two concentric spherical shells. If A is given a charge +Q while B is earthed as shown in figure then
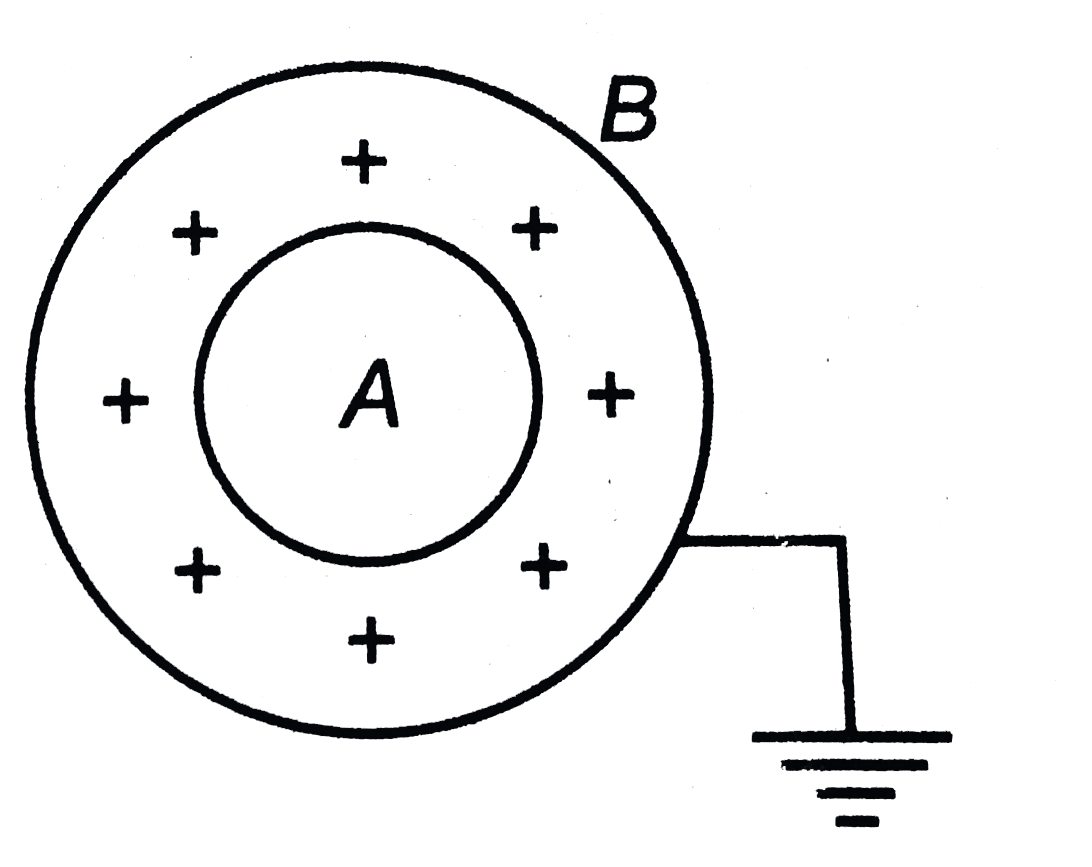
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then

View SolutionThree concentric metallic spherical shells A,B and C of radii a,b and c(a<b<c) have surface charge densities +σ,−σand +σ respectively ,the potential of shell B is
View SolutionConsider two concentric metal spheres. The outer sphere is given a charge Q>0, then
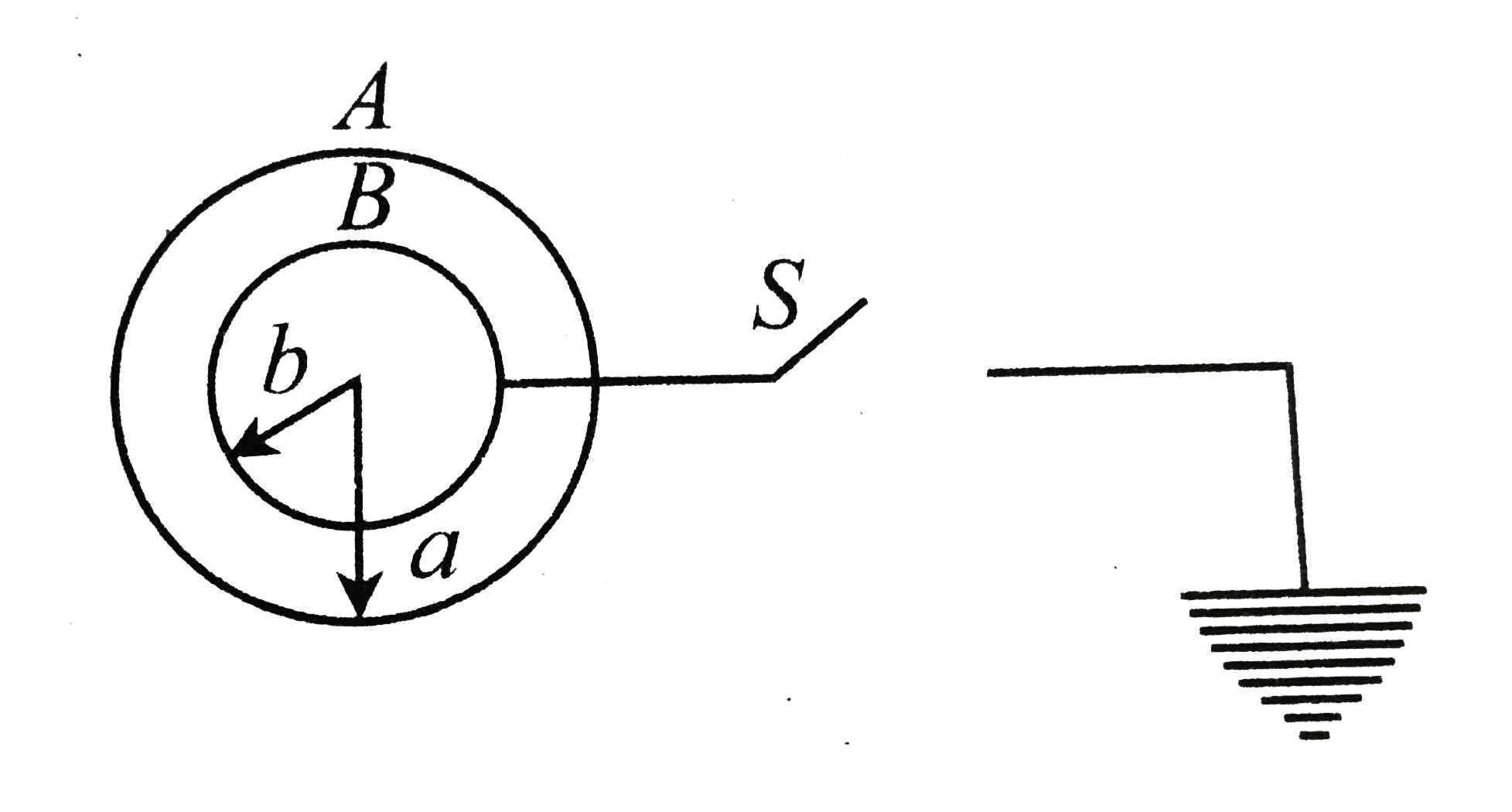 ,
,
View SolutionTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

Choose the correct optin (K=14πε0)
View SolutionTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

If we draw a graph between potential V and distance r from the centre, the graph will be like
View Solution
