Charges are placed 1 m apart. Work done to bring these charges at a distance 0.5 m from each other is
The correct Answer is:D
To solve the problem of calculating the work done to bring two charges from a distance of 1 meter to 0.5 meters apart, we can follow these steps:
1. Identify the Charges and Constants:
- Let Q1=5μC=5×10−6C
- Let Q2=10μC=10×10−6C
- The electrostatic constant k=9×109N⋅m2/C2
2. Calculate Initial Potential Energy:
- The initial distance ri=1m
- The formula for potential energy U between two point charges is given by:
U=k⋅Q1⋅Q2r
- Substituting the values for initial potential energy:
Ui=9×109⋅(5×10−6)⋅(10×10−6)1
- Calculate Ui:
Ui=9×109⋅50×10−121=9×50×10−3=450×10−3J=0.45J
3. Calculate Final Potential Energy:
- The final distance rf=0.5m
- Now calculate the final potential energy:
Uf=9×109⋅(5×10−6)⋅(10×10−6)0.5
- Calculate Uf:
Uf=9×109⋅50×10−120.5=9×50×10−3×2=900×10−3J=0.9J
4. Calculate Work Done:
- The work done by the external agent is the change in potential energy:
W=Uf−Ui
- Substitute the values:
W=0.9J−0.45J=0.45J
5. Convert to Standard Form:
- The work done can also be expressed in microjoules:
W=0.45J=45×10−2J
Final Answer
The work done to bring the charges from a distance of 1 meter to 0.5 meters apart is:
W=0.45Jor45×10−2J
- Let Q1=5μC=5×10−6C
- Let Q2=10μC=10×10−6C
- The electrostatic constant k=9×109N⋅m2/C2
- The initial distance ri=1m
- The formula for potential energy U between two point charges is given by:
U=k⋅Q1⋅Q2r
- Substituting the values for initial potential energy:
Ui=9×109⋅(5×10−6)⋅(10×10−6)1
- Calculate Ui:
Ui=9×109⋅50×10−121=9×50×10−3=450×10−3J=0.45J
- The final distance rf=0.5m
- Now calculate the final potential energy:
Uf=9×109⋅(5×10−6)⋅(10×10−6)0.5
- Calculate Uf:
Uf=9×109⋅50×10−120.5=9×50×10−3×2=900×10−3J=0.9J
- The work done by the external agent is the change in potential energy:
W=Uf−Ui
- Substitute the values:
W=0.9J−0.45J=0.45J
- The work done can also be expressed in microjoules:
W=0.45J=45×10−2J
The work done to bring the charges from a distance of 1 meter to 0.5 meters apart is:
W=0.45Jor45×10−2J
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View SolutionTwo charges +20μCand−20μC are placed 10mm apart. The electric field at point P, on the axis of the dipole 10 cm away from its centre O on the side of the positive charge is
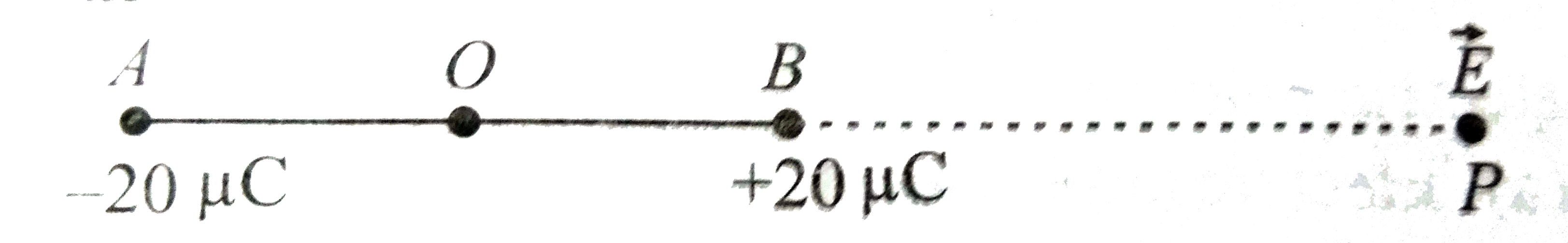
View Solution
Knowledge Check
Two point charges of 1μCand−1μC are separated by a distance of 100 Å. A point P is at a distance of 10 cm from the midpoint and on the perpendicular bisector of the line joining the two charges. The electric field at P will be
A9NC−1B0.9NC−1C90NC−1D0.09NC−1
Two charges +6μC and −4μC are placed 15 cm apart as shown. At what distance from A to its right the electronstatic potential is zero (distances in cm)

View SolutionTwo charges +6 'mu'C and -6 'mu'C are placed 15 cm apart as shown . At what distance from A to its right, the electrostatic potential is zero (distance in cm)

View SolutionTwo ball with charges 5μCand10μC are at a distance of 1 m from each other. In order to reduce the distance between them to 0.5 m , the amount of work to be performed is
View SolutionTwo charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric. field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
View Solutionfind the electric field strength due to a point charge of 5μC at a distance of 80 cm from the charge.
View SolutionTwo identicaln thin rings each of radius 10 cm carrying charges 10 C and 5 C are coaxially placed at a distance 10 cm apart. The work done in moving a charge q from the centre of the first ring to that of the second is
View SolutionTwo charges ±10μC are placed 5×10−3m apart. Determine the electric field at a point Q,0⋅15m away from O, on a line passing through O and normal to the axis of the dipole.
View Solution
