Two identicaln thin rings each of radius 10 cm carrying charges 10 C and 5 C are coaxially placed at a distance 10 cm apart. The work done in moving a charge q from the centre of the first ring to that of the second is
q8πε0.[√2+1√2]
q8πε0.[√2−1√2]
q4πε0.[√2+1√2]
q4πε0.[√2−1√2]
The correct Answer is:B
To solve the problem of finding the work done in moving a charge q from the center of the first ring to that of the second ring, we can follow these steps:
Step 1: Understand the Setup
We have two identical thin rings:
- Ring 1 has a charge Q1=10C and is located at the origin.
- Ring 2 has a charge Q2=5C and is located 10 cm away from Ring 1 along the axis.
Step 2: Calculate the Electric Potential at the Center of Each Ring
The electric potential V at a point due to a charged ring at a distance r from its center is given by the formula:
V=Q4πϵ0r
where Q is the charge, r is the distance from the center of the ring to the point where the potential is being calculated, and ϵ0 is the permittivity of free space.
For Ring 1 (at its center):
- The distance r1=0 (since we are at the center).
- The potential V1 due to Ring 1 is:
V1=Q14πϵ0r1=104πϵ0⋅0(undefined, but we consider the potential at the center)
For Ring 2 (at its center):
- The distance r2=10cm=0.1m.
- The potential V2 due to Ring 2 is:
V2=Q24πϵ0r2=54πϵ0⋅0.1
Step 3: Calculate the Total Potential at Each Point
The total potential at the center of Ring 1, considering the influence of Ring 2, is:
V_1 = \frac{Q_1}{4 \pi \epsilon_0 \cdot 0} + \frac{Q_2}{4 \pi \epsilon_0 \cdot r_{12}} \quad \text{(where r_{12} is the distance from Ring 2 to Ring 1)}
For r12=10cm=0.1m:
V1=104πϵ0⋅0+54πϵ0⋅0.1
The total potential at the center of Ring 2 is:
V_2 = \frac{Q_2}{4 \pi \epsilon_0 \cdot 0} + \frac{Q_1}{4 \pi \epsilon_0 \cdot r_{21}} \quad \text{(where r_{21} is the distance from Ring 1 to Ring 2)}
For r21=10cm=0.1m:
V2=54πϵ0⋅0+104πϵ0⋅0.1
Step 4: Calculate the Work Done
The work done W in moving a charge q from the center of Ring 1 to the center of Ring 2 is given by:
W=q(V2−V1)
Step 5: Substitute Values and Simplify
Substituting the values we calculated for V1 and V2:
W=q((54πϵ0⋅0.1)−(104πϵ0⋅0))
Final Result
After simplifying the expression, we find the work done in moving the charge q from the center of the first ring to the center of the second ring.
We have two identical thin rings:
- Ring 1 has a charge Q1=10C and is located at the origin.
- Ring 2 has a charge Q2=5C and is located 10 cm away from Ring 1 along the axis.
The electric potential V at a point due to a charged ring at a distance r from its center is given by the formula:
V=Q4πϵ0r
where Q is the charge, r is the distance from the center of the ring to the point where the potential is being calculated, and ϵ0 is the permittivity of free space.
- The distance r1=0 (since we are at the center).
- The potential V1 due to Ring 1 is:
V1=Q14πϵ0r1=104πϵ0⋅0(undefined, but we consider the potential at the center)
- The distance r2=10cm=0.1m.
- The potential V2 due to Ring 2 is:
V2=Q24πϵ0r2=54πϵ0⋅0.1
The total potential at the center of Ring 1, considering the influence of Ring 2, is:
V_1 = \frac{Q_1}{4 \pi \epsilon_0 \cdot 0} + \frac{Q_2}{4 \pi \epsilon_0 \cdot r_{12}} \quad \text{(where r_{12} is the distance from Ring 2 to Ring 1)}
For r12=10cm=0.1m:
V1=104πϵ0⋅0+54πϵ0⋅0.1
V_2 = \frac{Q_2}{4 \pi \epsilon_0 \cdot 0} + \frac{Q_1}{4 \pi \epsilon_0 \cdot r_{21}} \quad \text{(where r_{21} is the distance from Ring 1 to Ring 2)}
For r21=10cm=0.1m:
V2=54πϵ0⋅0+104πϵ0⋅0.1
The work done W in moving a charge q from the center of Ring 1 to the center of Ring 2 is given by:
W=q(V2−V1)
Substituting the values we calculated for V1 and V2:
W=q((54πϵ0⋅0.1)−(104πϵ0⋅0))
After simplifying the expression, we find the work done in moving the charge q from the center of the first ring to the center of the second ring.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View Solution
Knowledge Check
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Two identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View SolutionTwo charges −10C and +10C are placed 10 cm apart. Potential at the centre of th eline joining the two charges is
View SolutionTwo positive point charges of 12μC and 8μC are 10cm apart. The work done in bringing then 4cm closer is
View SolutionTwo positive point charges of 12μC and 8μC are 10cm apart. The work done in bringing then 4cm closer is
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View SolutionTwo charged particles are placed at a distance 1.0 cm apart. What is the minimum possible magnitude of the electric force acting o each charge?
View SolutionTwo thin rings each of radius R are placed at a distance 'd' apart. The charges on the rings are +q and -q. The potential difference between their centres will be -
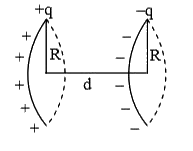
View Solution
